对数函数 第一课时(江苏省南京市)
图片预览








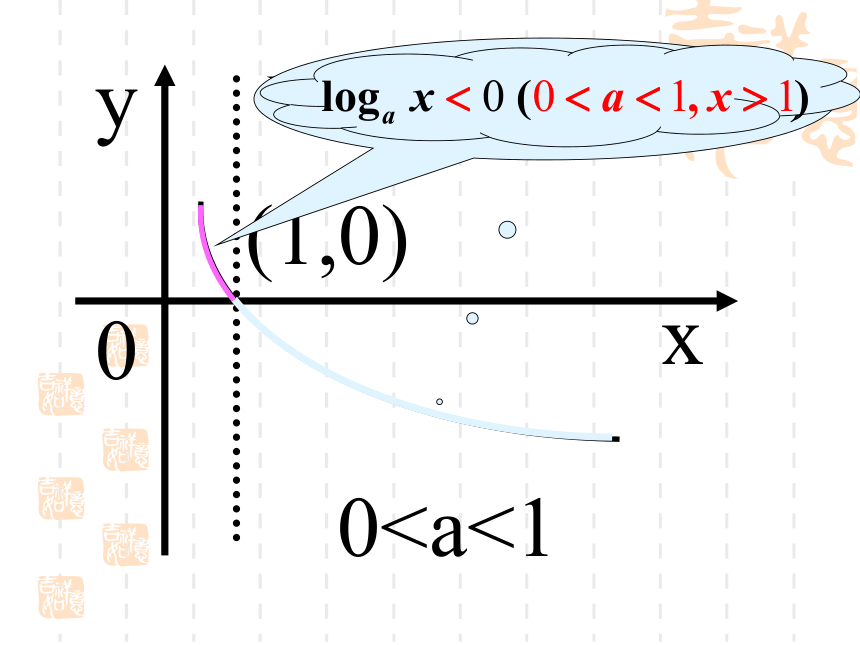

文档简介
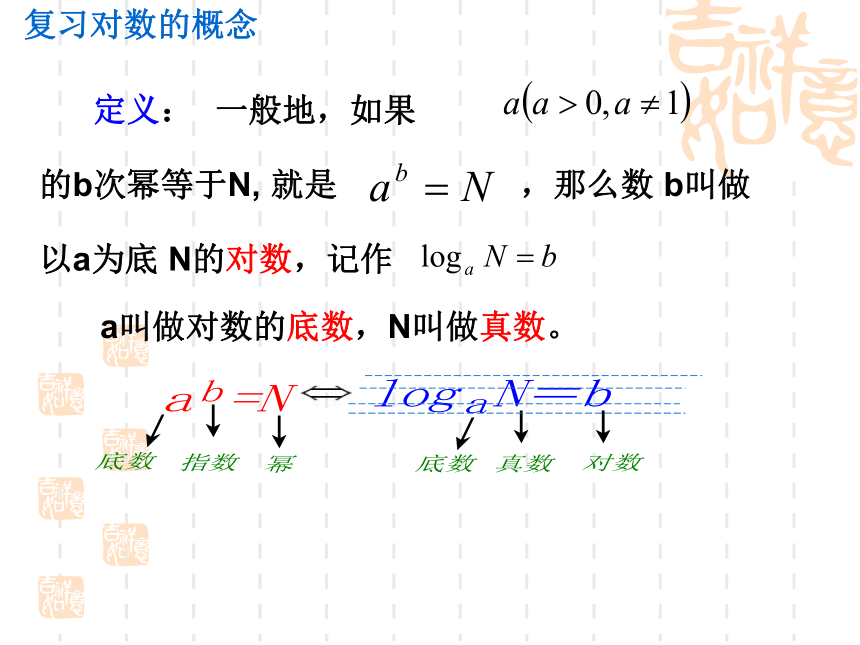
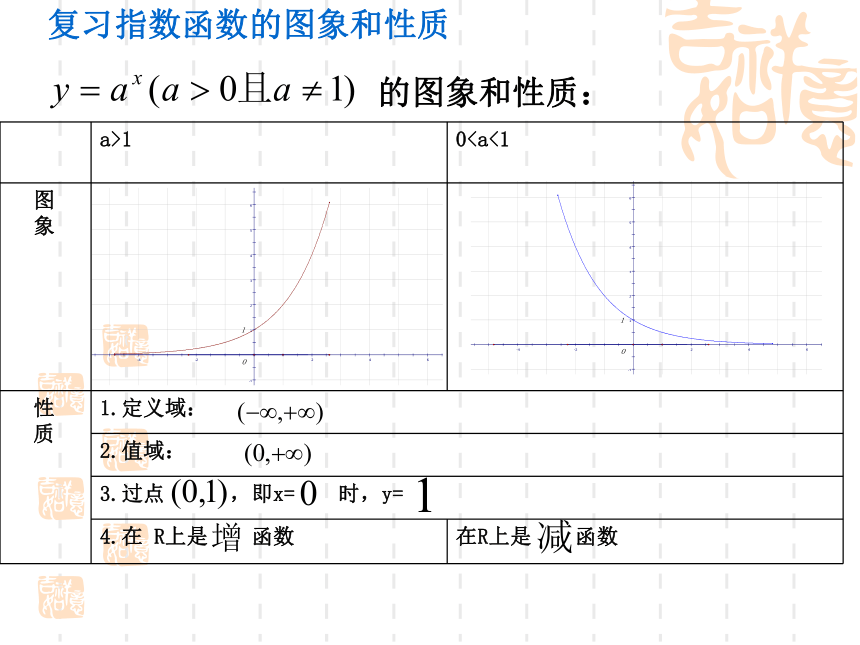
课件31张PPT。对数函数(1) 一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 a叫做对数的底数,N叫做真数。定义:复习对数的概念⑴负数与零没有对数⑵ ⑶对数恒等式复习对数的性质⑷常用对数: =lgN⑸自然对数: =lnN(6)底数a的取值范围: 真数N的取值范围 :复习对数运算法则的图象和性质: 复习指数函数的图象和性质某种细胞分裂时,由一个分裂成2个,由2个分成4个……。一个这样的细胞分裂x次以后,得到的细胞个数y与分裂次数x的函数关系式可表示为 .y = 2 x
对数函数的定义:新课讲解.温帮知新知识巩固课堂小结课外作业学习进程1函数 y = log a x (a>0,a≠1)叫做对数函数.
其中x是自变量
函数y = log a x 与函数y = a x (a>0,a≠1)定义域、值域相反函数的定义域是(0,+∞)a>1(1,0)X=10因为指数函数y=ax (0 XYO112233445567Y=log2xY=XY=2x-1-1-2●●●●●●●●●
●
新授内容: 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3) 解 :由 得 ∴函数 的定义域是讲解范例 (1) 解 :例2求下列函数的反函数(1) (2) (2) 例3 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: (1) (2)考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是 练习 1.画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: y轴右方,都经过点(1,0),
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.练习 2.求下列函数的定义域:(1)(2)(3)(4)小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减小结 :课后作业: P85 习题2.8 1,2,3祝同学们心情愉快!^_^ (*^__^*)
对数函数的定义:新课讲解.温帮知新知识巩固课堂小结课外作业学习进程1函数 y = log a x (a>0,a≠1)叫做对数函数.
其中x是自变量
函数y = log a x 与函数y = a x (a>0,a≠1)定义域、值域相反函数的定义域是(0,+∞)a>1(1,0)X=10
●
新授内容: 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3) 解 :由 得 ∴函数 的定义域是讲解范例 (1) 解 :例2求下列函数的反函数(1) (2) (2) 例3 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: (1) (2)考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是 练习 1.画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: y轴右方,都经过点(1,0),
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.练习 2.求下列函数的定义域:(1)(2)(3)(4)小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减小结 :课后作业: P85 习题2.8 1,2,3祝同学们心情愉快!^_^ (*^__^*)
