山东省泰安市2014年鲁教版初四数学第5单元确定圆的条件和圆的切线练习题
文档属性
| 名称 | 山东省泰安市2014年鲁教版初四数学第5单元确定圆的条件和圆的切线练习题 |
|
|
| 格式 | zip | ||
| 文件大小 | 210.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-05 00:00:00 | ||
图片预览



文档简介
鲁教版五四制初四数学第5单元确定圆的条件和圆的切线练习题
一.选择题(共15小题)
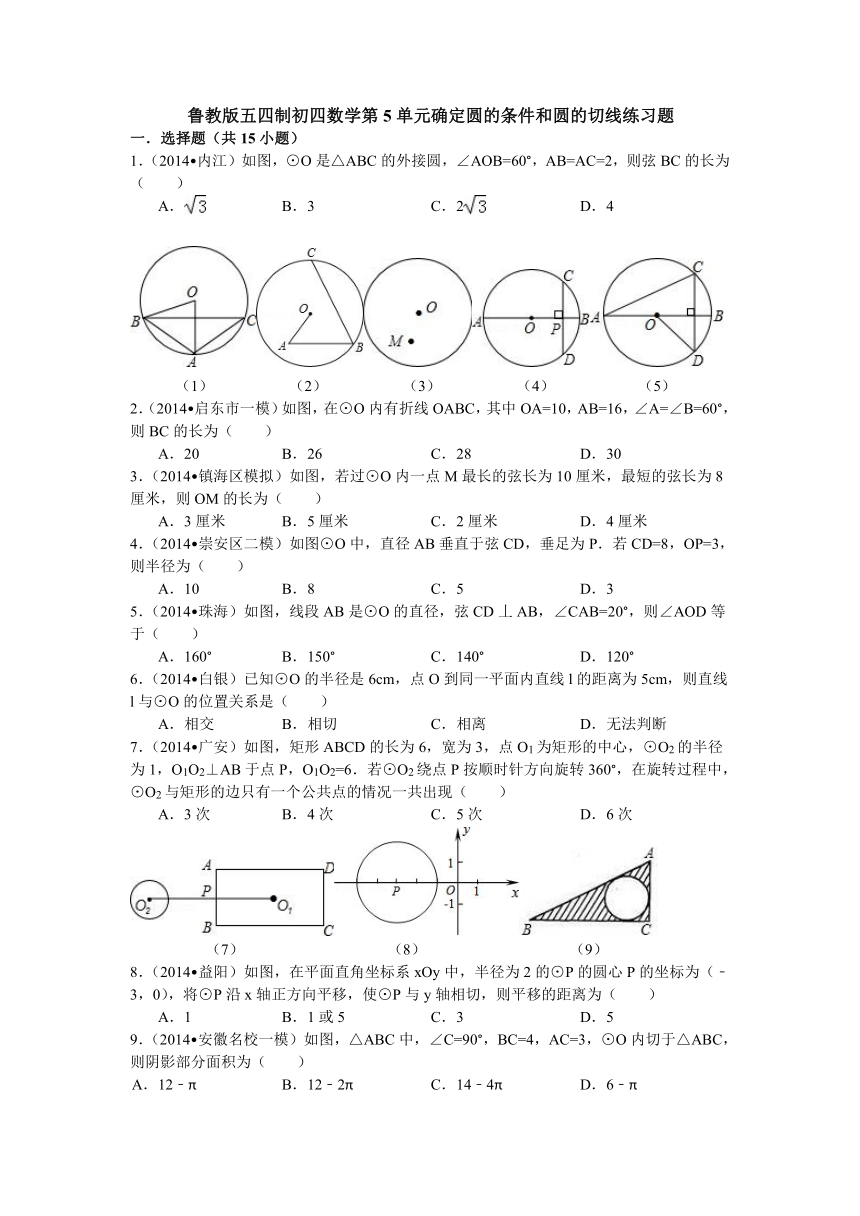
1.(2014 内江)如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B. 3 C. 2 D. 4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3) (4) (5)
2.(2014 启东市一模)如图,在⊙O内有折线OABC,其中OA=10,AB=16,∠A=∠B=60°,则BC的长为( )
A.20 B. 26 C. 28 D. 30
3.(2014 镇海区模拟)如图,若过⊙O内一点M最长的弦长为10厘米,最短的弦长为8厘米,则OM的长为( )
A.3厘米 B. 5厘米 C. 2厘米 D. 4厘米
4.(2014 崇安区二模)如图⊙O中,直径AB垂直于弦CD,垂足为P.若CD=8,OP=3,则半径为( )
A.10 B. 8 C. 5 D. 3
5.(2014 珠海)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.160° B. 150° C. 140° D. 120°
6.(2014 白银)已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是( )
A.相交 B. 相切 C. 相离 D. 无法判断
7.(2014 广安)如图,矩形ABCD ( http: / / www.21cnjy.com )的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
A.3次 B. 4次 C. 5次 D. 6次
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(7) (8) (9)
8.(2014 益阳)如图,在平面直角坐标 ( http: / / www.21cnjy.com )系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B. 1或5 C. 3 D. 5
9.(2014 安徽名校一模)如图,△ABC中,∠C=90°,BC=4,AC=3,⊙O内切于△ABC,则阴影部分面积为( )
A. 12﹣π B. 12﹣2π C. 14﹣4π D. 6﹣π
10.(2013 保定一模)如图⊙O是Rt△ABC的内切圆,D,E,F分别为切点,∠ACB=90°,则∠EDF的度数为( )
A.25° B. 30° C. 45° D. 60°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) (10) (11) (12) (13)
11.(2014 天津)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )
A.20° B. 25° C. 40° D. 50°
12.(2014 哈尔滨)如图,AB是⊙ ( http: / / www.21cnjy.com )O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
A.30° B. 25° C. 20° D. 15°
13.(2014 泰安)如 ( http: / / www.21cnjy.com )图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
14.(2014 内江)如图,Rt△A ( http: / / www.21cnjy.com )BC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )
A.2.5 B. 1.6 C. 1.5 D. 1
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(14) (15) (16)
15.(2014 江阴市二模)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为 ( )
A.40° B. 50° C. 55° D. 60°
二.填空题(共7小题)
16.(2014 抚州)如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为 ________ .
17.(2010 潮阳区模拟)如图 ( http: / / www.21cnjy.com ),四边形ABCD为圆的内接四边形,DA、CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (18) (19)
18.(2014 湘潭)如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA= _________ .
19.(2014 青岛)如图,AB ( http: / / www.21cnjy.com )是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 _________ °.
20.(2014 天水)如图,PA,PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=50°,则∠P= _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(20) (21) (22)
21.(2014 南充)如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是 _________ .(结果保留π)
22.(2014 成都)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C= _________ 度.
三.解答题(共8小题)
23.(2014 黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
( http: / / www.21cnjy.com )
24.(2014 陕西)如 ( http: / / www.21cnjy.com )图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
( http: / / www.21cnjy.com )
25.(2014 新疆)如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2,求⊙O的半径.
( http: / / www.21cnjy.com )
26.(2014 攀枝花)如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若AB=13,sinB=,求CE的长.
( http: / / www.21cnjy.com )
27.(2014 汕尾)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
( http: / / www.21cnjy.com )
28.(2014 宿迁)如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为,OP=1,求BC的长.
( http: / / www.21cnjy.com )
29.(2014 白银)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
( http: / / www.21cnjy.com )
30.(2014 梅州)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=4,求⊙O的面积.
( http: / / www.21cnjy.com )
鲁教版五四制初四数学第5单元确定圆的条件和圆的切线练习题
参考答案
一.选择题(共15小题)
1.C.2.B.3.A.4.C.5.C.6.A.7.B.8.B.9.D.10.C.11.C.
12.B.13.A.14.B.15.C.
二.填空题(共7小题)
16. 70° .17. 70° .18. 4 .19. 35 °20. 80° .
21. 16π .22. 40
三.解答题(共8小题)
23.(1)证明:连接OD,∵AC是直径,∠ACB=90°,
∴BC是⊙O的切线,∠BCA=90°.
又∵DE是⊙O的切线,∴ED=EC,∠ODE=90°,∴∠ODA+∠EDB=90°,
∵OA=OD,∴∠OAD=∠ODA,
又∵∠OAD+∠DBE=90°,∴∠EDB=∠EBD,∴ED=EB,∴EB=EC.
(2)解:当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,
又∵ED=EB,∴△DEB是等腰直角三角形,则∠B=45°,
∴△ABC是等腰直角三角形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(23) (24) (25) (26)
24.(1)证明:连接OD,
∵BD是⊙O的切线,∴OD⊥BD,
∵AC⊥BD,∴OD∥AC,∴∠2=∠3,
∵OA=OD,∴∠1=∠3,∴∠1=∠2,即AD平分∠BAC;
(2)解:∵OD∥AC,∴△BOD∽△BAC,∴,∴,解得:AC=.
25.(1)证明:连结OC,如图,
∵=,∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AF,
∵CD⊥AF,∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,∵AB为直径,∴∠ACB=90°,
∵==,∴∠BOC=×180°=60°,∴∠BAC=30°,∴∠DAC=30°,
在Rt△ADC中,CD=2,∴AC=2CD=4,
在Rt△ACB中,BC=AC=×4=4,∴AB=2BC=8,
∴⊙O的半径为4.
26.(1)证明:连接AD,
∵AB是⊙O的直径,∴∠ADB=90°∴AD⊥BC,又D是BC的中点,∴AB=AC;
(2)证明:连接OD,∵O、D分别是AB、BC的中点,∴OD∥AC,
∴∠ODE=∠DEC=90°,∴OD⊥DE,∴DE是⊙O的切线;
(3)解:∵AB=13,sinB=,∴=,∴AD=12,∴由勾股定理得BD=5,∴CD=5,
∵∠B=∠C,∴=,∴DE=,∴根据勾股定理得CE=.
27.证明:(1)如图,连接OD.
∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.
又∵OD=OC,∴∠ODC=∠OCD,∴∠EDC=∠ECD,∴ED=EC;
∵AC为直径,∴∠ADC=90°,∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,
∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,
又∵∠B=∠B∴△ABC∽△CDB,∴,∴BC2=BD BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,∴∠ADC=90°,
∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(27) (28) (29) (30)
28.(1)证明:连结OB,如图,
∵OP⊥OA,∴∠AOP=90°,∴∠A+∠APO=90°,
∵CP=CB,∴∠CBP=∠CPB,而∠CPB=∠APO,∴∠APO=∠CBP,
∵OA=OB,∴∠A=∠OBA,∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,在Rt△OBC中,OB=,OC=CP+OP=x+1,
∵OB2+BC2=OC2,∴()2+x2=(x+1)2,解得x=2,
即BC的长为2.
29.(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,
∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.
30.(1)证明:连接OC,∵在△ABO中,OA=OB,C是边AB的中点,∴OC⊥AB,
∵以O为圆心的圆过点C,∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°,∴∠A=∠B=30°,
∵AB=4,C是边AB的中点,∴AC=AB=2,∴OC=AC tan∠A=2×=2,
∴⊙O的面积为:π×22=4π.
一.选择题(共15小题)
1.(2014 内江)如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B. 3 C. 2 D. 4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3) (4) (5)
2.(2014 启东市一模)如图,在⊙O内有折线OABC,其中OA=10,AB=16,∠A=∠B=60°,则BC的长为( )
A.20 B. 26 C. 28 D. 30
3.(2014 镇海区模拟)如图,若过⊙O内一点M最长的弦长为10厘米,最短的弦长为8厘米,则OM的长为( )
A.3厘米 B. 5厘米 C. 2厘米 D. 4厘米
4.(2014 崇安区二模)如图⊙O中,直径AB垂直于弦CD,垂足为P.若CD=8,OP=3,则半径为( )
A.10 B. 8 C. 5 D. 3
5.(2014 珠海)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.160° B. 150° C. 140° D. 120°
6.(2014 白银)已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是( )
A.相交 B. 相切 C. 相离 D. 无法判断
7.(2014 广安)如图,矩形ABCD ( http: / / www.21cnjy.com )的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
A.3次 B. 4次 C. 5次 D. 6次
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(7) (8) (9)
8.(2014 益阳)如图,在平面直角坐标 ( http: / / www.21cnjy.com )系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B. 1或5 C. 3 D. 5
9.(2014 安徽名校一模)如图,△ABC中,∠C=90°,BC=4,AC=3,⊙O内切于△ABC,则阴影部分面积为( )
A. 12﹣π B. 12﹣2π C. 14﹣4π D. 6﹣π
10.(2013 保定一模)如图⊙O是Rt△ABC的内切圆,D,E,F分别为切点,∠ACB=90°,则∠EDF的度数为( )
A.25° B. 30° C. 45° D. 60°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) (10) (11) (12) (13)
11.(2014 天津)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )
A.20° B. 25° C. 40° D. 50°
12.(2014 哈尔滨)如图,AB是⊙ ( http: / / www.21cnjy.com )O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
A.30° B. 25° C. 20° D. 15°
13.(2014 泰安)如 ( http: / / www.21cnjy.com )图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
14.(2014 内江)如图,Rt△A ( http: / / www.21cnjy.com )BC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )
A.2.5 B. 1.6 C. 1.5 D. 1
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(14) (15) (16)
15.(2014 江阴市二模)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为 ( )
A.40° B. 50° C. 55° D. 60°
二.填空题(共7小题)
16.(2014 抚州)如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为 ________ .
17.(2010 潮阳区模拟)如图 ( http: / / www.21cnjy.com ),四边形ABCD为圆的内接四边形,DA、CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (18) (19)
18.(2014 湘潭)如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA= _________ .
19.(2014 青岛)如图,AB ( http: / / www.21cnjy.com )是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 _________ °.
20.(2014 天水)如图,PA,PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=50°,则∠P= _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(20) (21) (22)
21.(2014 南充)如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是 _________ .(结果保留π)
22.(2014 成都)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C= _________ 度.
三.解答题(共8小题)
23.(2014 黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
( http: / / www.21cnjy.com )
24.(2014 陕西)如 ( http: / / www.21cnjy.com )图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
( http: / / www.21cnjy.com )
25.(2014 新疆)如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2,求⊙O的半径.
( http: / / www.21cnjy.com )
26.(2014 攀枝花)如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若AB=13,sinB=,求CE的长.
( http: / / www.21cnjy.com )
27.(2014 汕尾)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
( http: / / www.21cnjy.com )
28.(2014 宿迁)如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为,OP=1,求BC的长.
( http: / / www.21cnjy.com )
29.(2014 白银)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
( http: / / www.21cnjy.com )
30.(2014 梅州)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=4,求⊙O的面积.
( http: / / www.21cnjy.com )
鲁教版五四制初四数学第5单元确定圆的条件和圆的切线练习题
参考答案
一.选择题(共15小题)
1.C.2.B.3.A.4.C.5.C.6.A.7.B.8.B.9.D.10.C.11.C.
12.B.13.A.14.B.15.C.
二.填空题(共7小题)
16. 70° .17. 70° .18. 4 .19. 35 °20. 80° .
21. 16π .22. 40
三.解答题(共8小题)
23.(1)证明:连接OD,∵AC是直径,∠ACB=90°,
∴BC是⊙O的切线,∠BCA=90°.
又∵DE是⊙O的切线,∴ED=EC,∠ODE=90°,∴∠ODA+∠EDB=90°,
∵OA=OD,∴∠OAD=∠ODA,
又∵∠OAD+∠DBE=90°,∴∠EDB=∠EBD,∴ED=EB,∴EB=EC.
(2)解:当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,
又∵ED=EB,∴△DEB是等腰直角三角形,则∠B=45°,
∴△ABC是等腰直角三角形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(23) (24) (25) (26)
24.(1)证明:连接OD,
∵BD是⊙O的切线,∴OD⊥BD,
∵AC⊥BD,∴OD∥AC,∴∠2=∠3,
∵OA=OD,∴∠1=∠3,∴∠1=∠2,即AD平分∠BAC;
(2)解:∵OD∥AC,∴△BOD∽△BAC,∴,∴,解得:AC=.
25.(1)证明:连结OC,如图,
∵=,∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AF,
∵CD⊥AF,∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,∵AB为直径,∴∠ACB=90°,
∵==,∴∠BOC=×180°=60°,∴∠BAC=30°,∴∠DAC=30°,
在Rt△ADC中,CD=2,∴AC=2CD=4,
在Rt△ACB中,BC=AC=×4=4,∴AB=2BC=8,
∴⊙O的半径为4.
26.(1)证明:连接AD,
∵AB是⊙O的直径,∴∠ADB=90°∴AD⊥BC,又D是BC的中点,∴AB=AC;
(2)证明:连接OD,∵O、D分别是AB、BC的中点,∴OD∥AC,
∴∠ODE=∠DEC=90°,∴OD⊥DE,∴DE是⊙O的切线;
(3)解:∵AB=13,sinB=,∴=,∴AD=12,∴由勾股定理得BD=5,∴CD=5,
∵∠B=∠C,∴=,∴DE=,∴根据勾股定理得CE=.
27.证明:(1)如图,连接OD.
∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.
又∵OD=OC,∴∠ODC=∠OCD,∴∠EDC=∠ECD,∴ED=EC;
∵AC为直径,∴∠ADC=90°,∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,
∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,
又∵∠B=∠B∴△ABC∽△CDB,∴,∴BC2=BD BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,∴∠ADC=90°,
∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(27) (28) (29) (30)
28.(1)证明:连结OB,如图,
∵OP⊥OA,∴∠AOP=90°,∴∠A+∠APO=90°,
∵CP=CB,∴∠CBP=∠CPB,而∠CPB=∠APO,∴∠APO=∠CBP,
∵OA=OB,∴∠A=∠OBA,∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,在Rt△OBC中,OB=,OC=CP+OP=x+1,
∵OB2+BC2=OC2,∴()2+x2=(x+1)2,解得x=2,
即BC的长为2.
29.(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,
∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.
30.(1)证明:连接OC,∵在△ABO中,OA=OB,C是边AB的中点,∴OC⊥AB,
∵以O为圆心的圆过点C,∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°,∴∠A=∠B=30°,
∵AB=4,C是边AB的中点,∴AC=AB=2,∴OC=AC tan∠A=2×=2,
∴⊙O的面积为:π×22=4π.
