24.3.2.1相似三角形的判定1(广东省佛山市顺德区)
文档属性
| 名称 | 24.3.2.1相似三角形的判定1(广东省佛山市顺德区) |  | |
| 格式 | rar | ||
| 文件大小 | 809.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-24 08:01:00 | ||
图片预览



文档简介
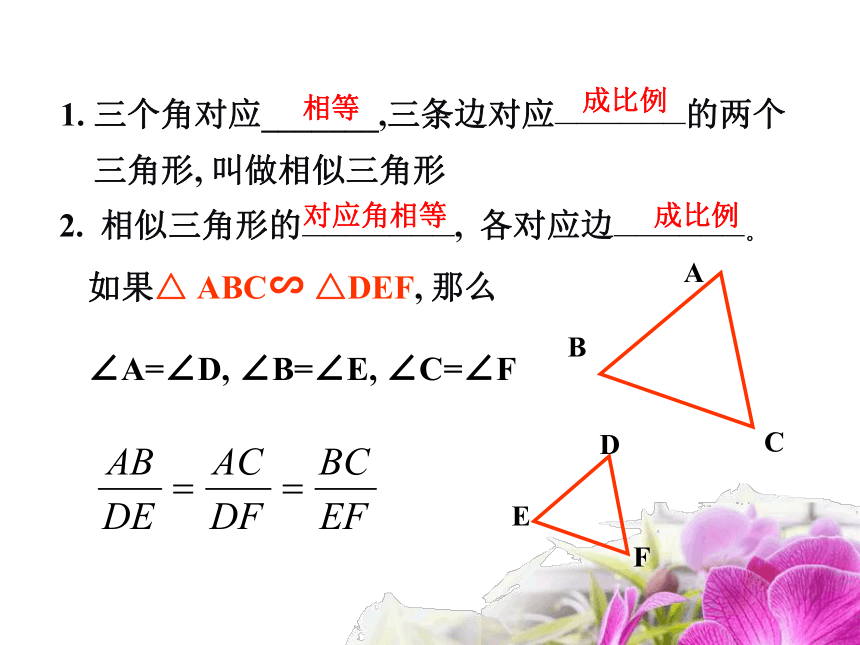
课件14张PPT。相似三角形的判定 1. 三个角对应_______,三条边对应——————的两个
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F1.任意画两个三角形△ABC, △A’B’C’,使其三组对角分别对应相等。2.用刻度尺量一量各边长,它们的对应边是否会成比例?与同伴交流,是否有相同结果。3.发现什么现象 ? 如果一个三角形的三个角与另一个三角形的三个角对应相等,那么这两个三角形相似。 探索根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
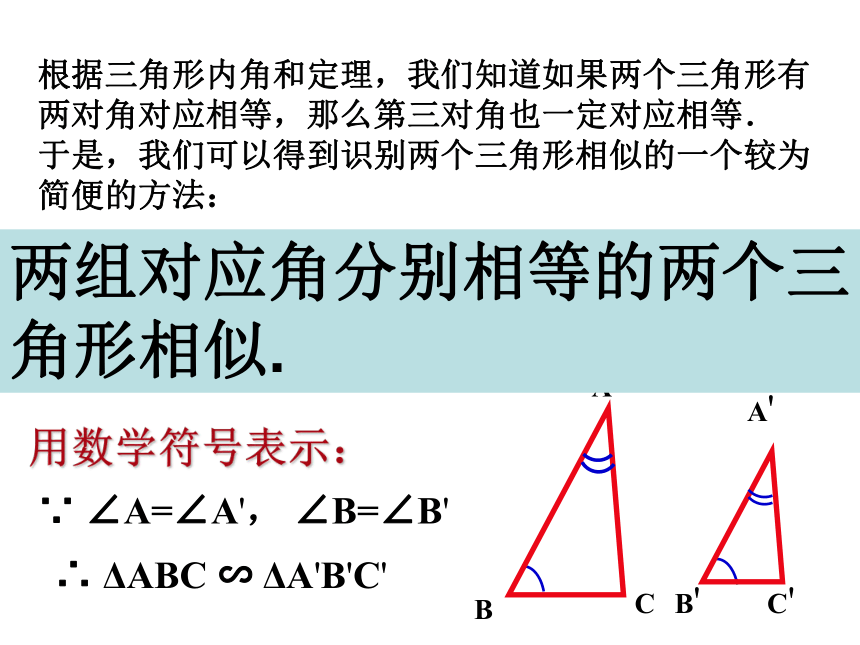
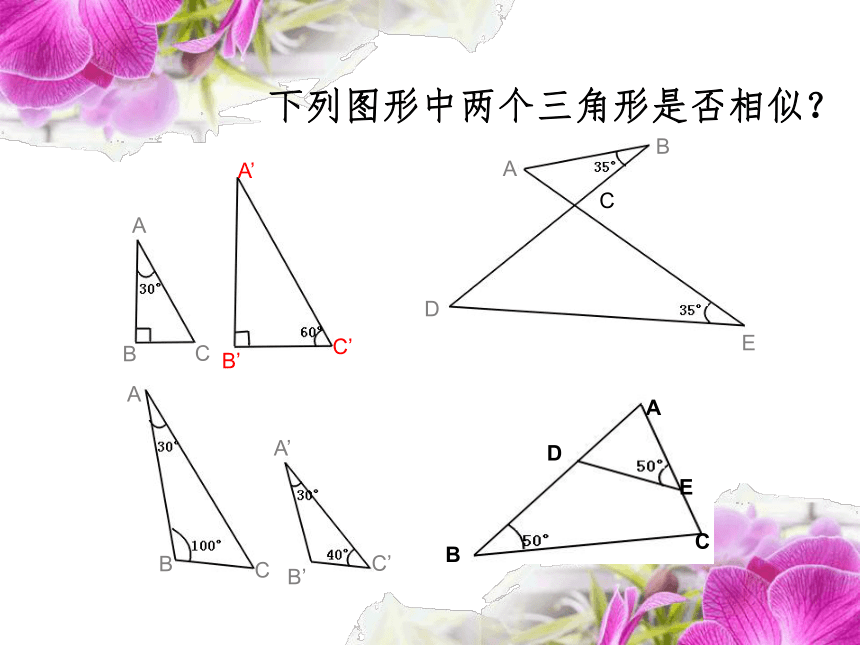
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'CC'两组对应角分别相等的两个三角形相似.下列图形中两个三角形是否相似?思 考能否再简便一些?
有一对角对应相等的两个三角形相似吗?
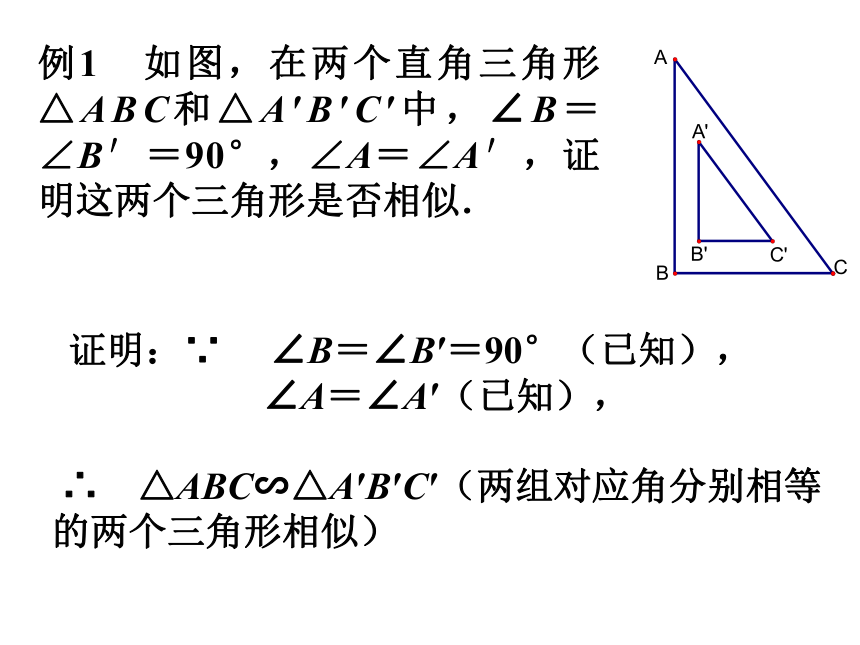
例1 如图,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,证明这两个三角形是否相似. 证明:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两组对应角分别相等的两个三角形相似) 例2: 如图18.3.5,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.证明: ∵ DE∥BC (已知) ∴ ∠AED=∠C (两直线平行,同位角相等), ∴ ∠CEF=∠A.(两直线平行,同位角相等)∴ △ADE∽△EFC. (两组对应角分别相等的两个三角形相似) 又∵ EF∥AB (已知) 如果点D恰好是边AB的中点,那么点E 是边AC的中点吗?
DE和BC又有什么关系? 练习
1.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
2.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;图2图33.在△ABC与△A′B′C′中,∠A=∠A′=50°,∠B=70°,∠B′=70°,这两个三角形相似吗?ABCA′ B′ C′ ∠A=∠A′=50° ∠B=70°∠B′=60°这两三角形仍然相似吗? 超级变变变:ABCA′ B′ C′ 作业P64页 第1,5题
《同步伴读》
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F1.任意画两个三角形△ABC, △A’B’C’,使其三组对角分别对应相等。2.用刻度尺量一量各边长,它们的对应边是否会成比例?与同伴交流,是否有相同结果。3.发现什么现象 ? 如果一个三角形的三个角与另一个三角形的三个角对应相等,那么这两个三角形相似。 探索根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'CC'两组对应角分别相等的两个三角形相似.下列图形中两个三角形是否相似?思 考能否再简便一些?
有一对角对应相等的两个三角形相似吗?
例1 如图,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,证明这两个三角形是否相似. 证明:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两组对应角分别相等的两个三角形相似) 例2: 如图18.3.5,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.证明: ∵ DE∥BC (已知) ∴ ∠AED=∠C (两直线平行,同位角相等), ∴ ∠CEF=∠A.(两直线平行,同位角相等)∴ △ADE∽△EFC. (两组对应角分别相等的两个三角形相似) 又∵ EF∥AB (已知) 如果点D恰好是边AB的中点,那么点E 是边AC的中点吗?
DE和BC又有什么关系? 练习
1.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
2.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;图2图33.在△ABC与△A′B′C′中,∠A=∠A′=50°,∠B=70°,∠B′=70°,这两个三角形相似吗?ABCA′ B′ C′ ∠A=∠A′=50° ∠B=70°∠B′=60°这两三角形仍然相似吗? 超级变变变:ABCA′ B′ C′ 作业P64页 第1,5题
《同步伴读》
