第11章三角形 单元达标测试题 2023—2024学年人教版八年级数学上册(含解析)
文档属性
| 名称 | 第11章三角形 单元达标测试题 2023—2024学年人教版八年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 537.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 18:59:19 | ||
图片预览


文档简介
2023-2024学年人教版八年级数学上册《第11章三角形》单元达标测试题(附答案)
一、单选题(满分32分)
1.一个多边形,它的内角和为,则这个多边形是( )
A.五边形 B.十边形 C.十二边形 D.不存在
2.一个多边形截去一个角后,得到的新多边形内角和为,则原多边形边数为( )
A.4 B.6 C.4或6 D.4或5或6
3.以下列各组线段为边,能组成三角形的是( )
A.3,3,4 B.4,9,5 C.5,18,8 D.9,15,3
4.如图,,,分别是的中线,角平分线和高,下列各式中错误的是( )
A. B.
C. D.
5.只使用下列正多边形中的一种铺满地面,这种正多边形可以是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
6.如图,在中,E是上的一点,,点D是的中点,记,,的面积分别为,,,且,则等于( )
A.1 B.2 C.3 D.4
7.如图,的中线相交于点,连接并延长交于点.以下结论一定正确的是( )
A. B. C. D.
8.如图,、是的角平分线,并且、交于点,若,则等于( )
A. B. C. D.
二、填空题(满分32分)
9.三角形按角分可以分为锐角三角形,直角三角形和 .
10.一个多边形的每一个外角都为,则这个多边形的边数是 .
11.已知,为的高线,为的角平分线,若,,则 度.
12.近日,中亚峰会于5月18日至19日在西安举行,暮色中的大唐芙蓉园流光溢彩,美轮美奂.工人师傅在楼阁上固定木制门框用来张贴欢迎条幅,为了防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是 .
13.如图,是的中线,E是的中点,连接,若的面积为5,则的面积为 .
14.在中,是高,,,若的面积为12,则线段的长度为 .
15.如图,若正五边形和长方形按如图方式叠放在一起,则的度数为 .
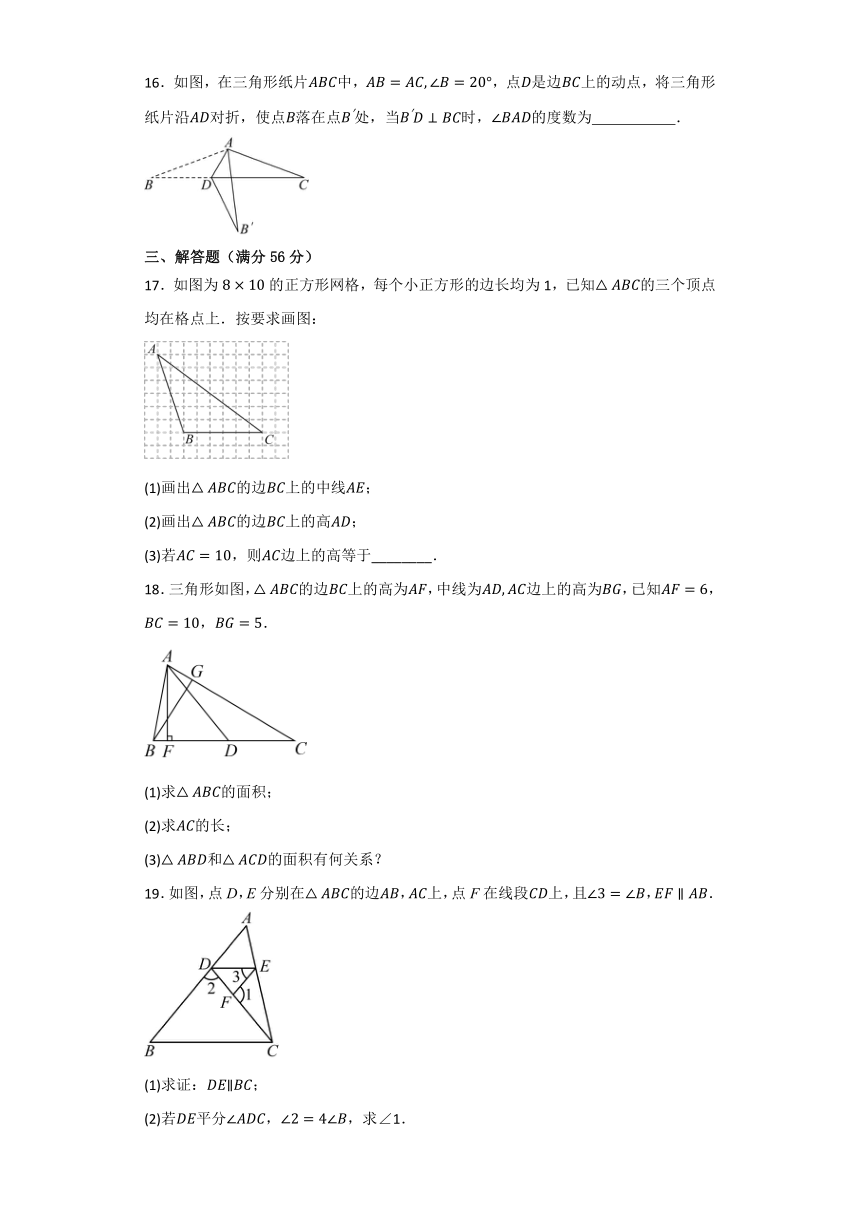
16.如图,在三角形纸片中,,点是边上的动点,将三角形纸片沿对折,使点落在点处,当时,的度数为 .
三、解答题(满分56分)
17.如图为的正方形网格,每个小正方形的边长均为1,已知的三个顶点均在格点上.按要求画图:
(1)画出的边上的中线;
(2)画出的边上的高;
(3)若,则边上的高等于________.
18.三角形如图,的边上的高为,中线为边上的高为,已知,,.
(1)求的面积;
(2)求的长;
(3)和的面积有何关系?
19.如图,点D,E分别在的边,上,点F在线段上,且,.
(1)求证:;
(2)若平分,,求∠1.
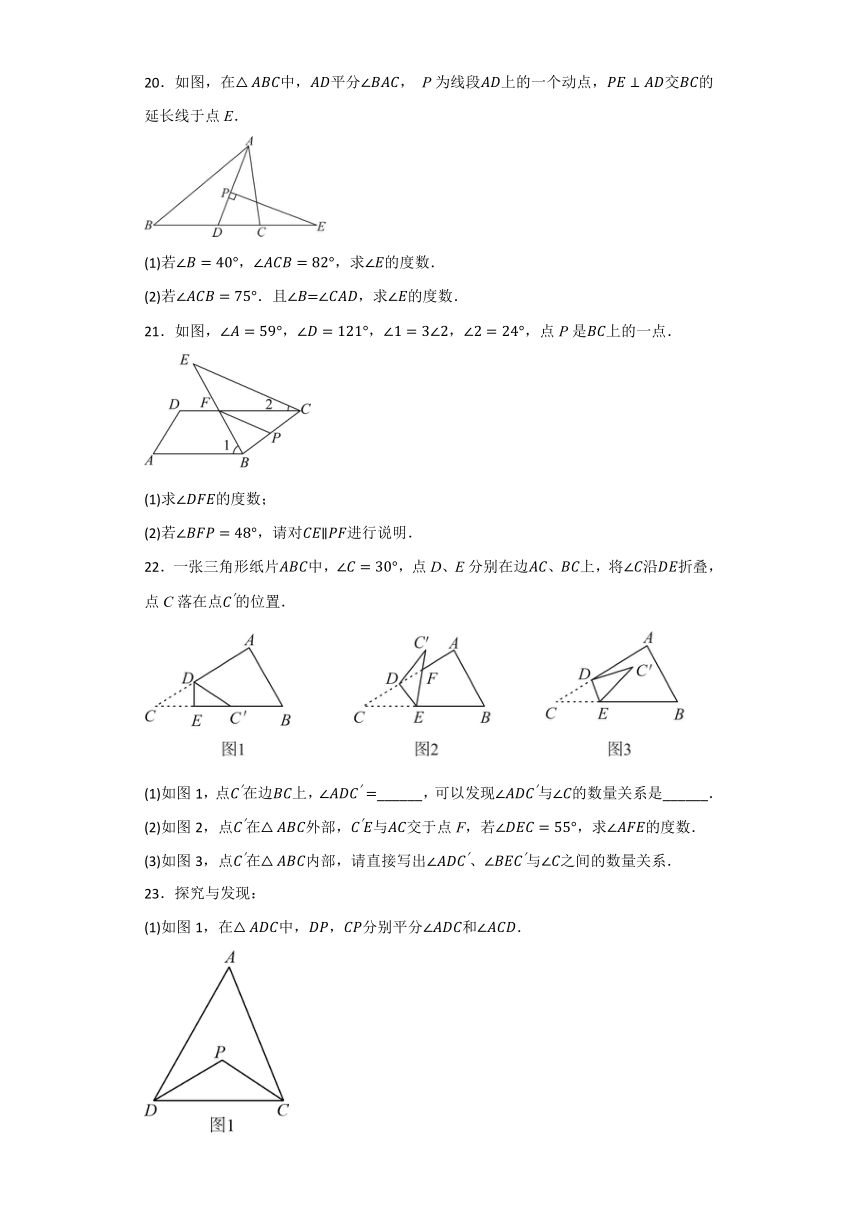
20.如图,在中,平分, P为线段上的一个动点,交的延长线于点E.
(1)若,,求的度数.
(2)若.且,求的度数.
21.如图,,点P是上的一点.
(1)求的度数;
(2)若,请对进行说明.
22.一张三角形纸片中,,点D、E分别在边、上,将沿折叠,点C落在点的位置.
(1)如图1,点在边上,______,可以发现与的数量关系是______.
(2)如图2,点在外部,与交于点F,若,求的度数.
(3)如图3,点在内部,请直接写出、与之间的数量关系.
23.探究与发现:
(1)如图1,在中,,分别平分和.
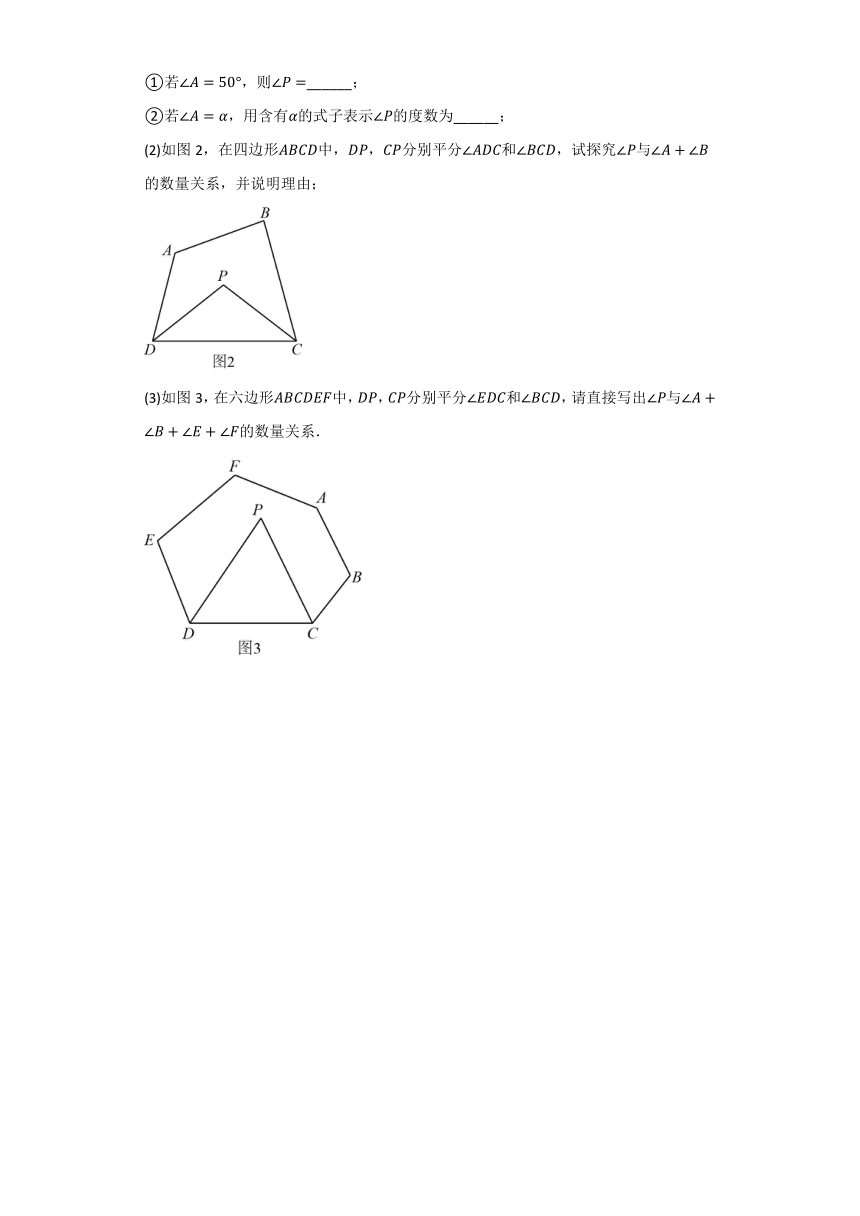
①若,则______;
②若,用含有的式子表示的度数为______;
(2)如图2,在四边形中,,分别平分和,试探究与的数量关系,并说明理由;
(3)如图3,在六边形中,,分别平分和,请直接写出与的数量关系.
参考答案
1.解:由题意得,
,
故选C.
2.解:设新多边形边数为n,
∵新多边形内角和为,
∴,
解得,
若多边形截去一个角,则会存在以下三种情况,多边形边数不变,增加1或减少1,如下图所示:
∴原多边形边数为4或5或6,
故选:D.
3.解:A、因为,则这三条线段能构成三角形,故本选项符合题意;
B、因为,则这三条线段不能构成三角形,故本选项不合题意;
C、因为,则这三条线段不能构成三角形,故本选项不合题意;
D、因为,则这三条线段不能构成三角形,故本选项不合题意;
故选:A.
4.解:∵,,分别是的中线,
∴,,,
∴,
而,
∴A,B,C都正确,D错误,
故选D
5.解:正六边形的每个内角为
∵
∴只使用正六边形可以铺满地面.
故选:B
6.解:连接,如图所示:
因为点D是的中点
又的高相等,
设
同理,
即:
设
,
又的高相等,
同理,
即:
解得:,则
故选:B
7.解:∵的中线相交于点,连接并延长交于点
∴也是的中线,
∴,
故选:B.
8.解:,
,
又、是的角平分线,
,
.
故选:B.
9.解:三角形按角的大小可分为锐角三角形、直角三角形、钝角三角形,
故答案为:钝角三角形.
10.解:因为一个多边形的每一个外角都等于,
所以这个多边形的边数为.
故答案为:10.
11.解:如图所示,当是锐角三角形时,
∵,,
∴
∵为的角平分线
∴
∵为的高线
∴,即
∴
∴
当是钝角三角形时,
∵,,
∴
∵为的角平分线
∴
∵为的高线
∴,即
∴
∴.
综上所述,或.
故答案为:或.
12.解:根据题意,为了防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是三角形具有稳定性,
故答案为:三角形具有稳定性.
13.解:是的中线,
,
,
,
是的中线,
,
,
故答案为:20.
14.解:当在内部时,如下图
根据题意可知:,
解得:
当在外部时,如下图
根据题意可知,
解得:
故答案为:3或5.
15.解:∵正五边形内角和为:,
∴,
∵长方形中,,
∴,
∴,
∴,
故答案为:36.
16.解:由折叠的性质得:;
∵,
∴;
①当在下方时,如图,
∵,
∴,
∴;
②当在上方时,如图,
∵,
∴,
∴;
综上,的度数为或;
故答案为:或.
17.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:设边上的高为h,
∵,
∴,
∴边上的高等于,
故答案为:.
18.(1)解:的面积;
(2)∵的面积,,
∴;
(3)∵为的中线,
∴,
∵的边上的高为,
∴.
即:和的面积相等.
19.(1)证明:∵
∴,
∵,
∴
∴,
(2)∵平分∠ADC,
∴,
由(1)知,
∴,
∵,,
∴,
∴,
又∵,
∴.
20.(1)解: ,,
,
平分,
,
,
又 ,
,
;
(2)设,
,
,
平分,
,
,
,
,
,
,
,
,
,
.
21.(1)解:∵,
∴,
∴,
∴,
∵,
∴;
(2)解:∵,,
∴,
∵,
∴.
22.解:(1)∵ 沿折叠,点C落在点的位置,,
∴,,
∴,
故答案为:,.
(2)∵沿折叠,点C落在点的位置,,,
∴,,
∴.
(3).理由如下:
连接,
∵沿折叠,点C落在点的位置,
∴,
∵,
∴.
23.(1)解:①,
.
,分别平分和,
,.
.
.
②,
.
,分别平分和,
,.
.
.
故答案为:
(2)解:,理由如下:
根据题意,得
.
,分别平分和,
,.
.
.
(3)解:.
理由如下:
根据题意,得
.
,分别平分和,
,.
.
.
一、单选题(满分32分)
1.一个多边形,它的内角和为,则这个多边形是( )
A.五边形 B.十边形 C.十二边形 D.不存在
2.一个多边形截去一个角后,得到的新多边形内角和为,则原多边形边数为( )
A.4 B.6 C.4或6 D.4或5或6
3.以下列各组线段为边,能组成三角形的是( )
A.3,3,4 B.4,9,5 C.5,18,8 D.9,15,3
4.如图,,,分别是的中线,角平分线和高,下列各式中错误的是( )
A. B.
C. D.
5.只使用下列正多边形中的一种铺满地面,这种正多边形可以是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
6.如图,在中,E是上的一点,,点D是的中点,记,,的面积分别为,,,且,则等于( )
A.1 B.2 C.3 D.4
7.如图,的中线相交于点,连接并延长交于点.以下结论一定正确的是( )
A. B. C. D.
8.如图,、是的角平分线,并且、交于点,若,则等于( )
A. B. C. D.
二、填空题(满分32分)
9.三角形按角分可以分为锐角三角形,直角三角形和 .
10.一个多边形的每一个外角都为,则这个多边形的边数是 .
11.已知,为的高线,为的角平分线,若,,则 度.
12.近日,中亚峰会于5月18日至19日在西安举行,暮色中的大唐芙蓉园流光溢彩,美轮美奂.工人师傅在楼阁上固定木制门框用来张贴欢迎条幅,为了防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是 .
13.如图,是的中线,E是的中点,连接,若的面积为5,则的面积为 .
14.在中,是高,,,若的面积为12,则线段的长度为 .
15.如图,若正五边形和长方形按如图方式叠放在一起,则的度数为 .
16.如图,在三角形纸片中,,点是边上的动点,将三角形纸片沿对折,使点落在点处,当时,的度数为 .
三、解答题(满分56分)
17.如图为的正方形网格,每个小正方形的边长均为1,已知的三个顶点均在格点上.按要求画图:
(1)画出的边上的中线;
(2)画出的边上的高;
(3)若,则边上的高等于________.
18.三角形如图,的边上的高为,中线为边上的高为,已知,,.
(1)求的面积;
(2)求的长;
(3)和的面积有何关系?
19.如图,点D,E分别在的边,上,点F在线段上,且,.
(1)求证:;
(2)若平分,,求∠1.
20.如图,在中,平分, P为线段上的一个动点,交的延长线于点E.
(1)若,,求的度数.
(2)若.且,求的度数.
21.如图,,点P是上的一点.
(1)求的度数;
(2)若,请对进行说明.
22.一张三角形纸片中,,点D、E分别在边、上,将沿折叠,点C落在点的位置.
(1)如图1,点在边上,______,可以发现与的数量关系是______.
(2)如图2,点在外部,与交于点F,若,求的度数.
(3)如图3,点在内部,请直接写出、与之间的数量关系.
23.探究与发现:
(1)如图1,在中,,分别平分和.
①若,则______;
②若,用含有的式子表示的度数为______;
(2)如图2,在四边形中,,分别平分和,试探究与的数量关系,并说明理由;
(3)如图3,在六边形中,,分别平分和,请直接写出与的数量关系.
参考答案
1.解:由题意得,
,
故选C.
2.解:设新多边形边数为n,
∵新多边形内角和为,
∴,
解得,
若多边形截去一个角,则会存在以下三种情况,多边形边数不变,增加1或减少1,如下图所示:
∴原多边形边数为4或5或6,
故选:D.
3.解:A、因为,则这三条线段能构成三角形,故本选项符合题意;
B、因为,则这三条线段不能构成三角形,故本选项不合题意;
C、因为,则这三条线段不能构成三角形,故本选项不合题意;
D、因为,则这三条线段不能构成三角形,故本选项不合题意;
故选:A.
4.解:∵,,分别是的中线,
∴,,,
∴,
而,
∴A,B,C都正确,D错误,
故选D
5.解:正六边形的每个内角为
∵
∴只使用正六边形可以铺满地面.
故选:B
6.解:连接,如图所示:
因为点D是的中点
又的高相等,
设
同理,
即:
设
,
又的高相等,
同理,
即:
解得:,则
故选:B
7.解:∵的中线相交于点,连接并延长交于点
∴也是的中线,
∴,
故选:B.
8.解:,
,
又、是的角平分线,
,
.
故选:B.
9.解:三角形按角的大小可分为锐角三角形、直角三角形、钝角三角形,
故答案为:钝角三角形.
10.解:因为一个多边形的每一个外角都等于,
所以这个多边形的边数为.
故答案为:10.
11.解:如图所示,当是锐角三角形时,
∵,,
∴
∵为的角平分线
∴
∵为的高线
∴,即
∴
∴
当是钝角三角形时,
∵,,
∴
∵为的角平分线
∴
∵为的高线
∴,即
∴
∴.
综上所述,或.
故答案为:或.
12.解:根据题意,为了防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是三角形具有稳定性,
故答案为:三角形具有稳定性.
13.解:是的中线,
,
,
,
是的中线,
,
,
故答案为:20.
14.解:当在内部时,如下图
根据题意可知:,
解得:
当在外部时,如下图
根据题意可知,
解得:
故答案为:3或5.
15.解:∵正五边形内角和为:,
∴,
∵长方形中,,
∴,
∴,
∴,
故答案为:36.
16.解:由折叠的性质得:;
∵,
∴;
①当在下方时,如图,
∵,
∴,
∴;
②当在上方时,如图,
∵,
∴,
∴;
综上,的度数为或;
故答案为:或.
17.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:设边上的高为h,
∵,
∴,
∴边上的高等于,
故答案为:.
18.(1)解:的面积;
(2)∵的面积,,
∴;
(3)∵为的中线,
∴,
∵的边上的高为,
∴.
即:和的面积相等.
19.(1)证明:∵
∴,
∵,
∴
∴,
(2)∵平分∠ADC,
∴,
由(1)知,
∴,
∵,,
∴,
∴,
又∵,
∴.
20.(1)解: ,,
,
平分,
,
,
又 ,
,
;
(2)设,
,
,
平分,
,
,
,
,
,
,
,
,
,
.
21.(1)解:∵,
∴,
∴,
∴,
∵,
∴;
(2)解:∵,,
∴,
∵,
∴.
22.解:(1)∵ 沿折叠,点C落在点的位置,,
∴,,
∴,
故答案为:,.
(2)∵沿折叠,点C落在点的位置,,,
∴,,
∴.
(3).理由如下:
连接,
∵沿折叠,点C落在点的位置,
∴,
∵,
∴.
23.(1)解:①,
.
,分别平分和,
,.
.
.
②,
.
,分别平分和,
,.
.
.
故答案为:
(2)解:,理由如下:
根据题意,得
.
,分别平分和,
,.
.
.
(3)解:.
理由如下:
根据题意,得
.
,分别平分和,
,.
.
.
