2023-2024学年人教版八年级数学上册12.1全等三角形 同步训练(含简单答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册12.1全等三角形 同步训练(含简单答案) | 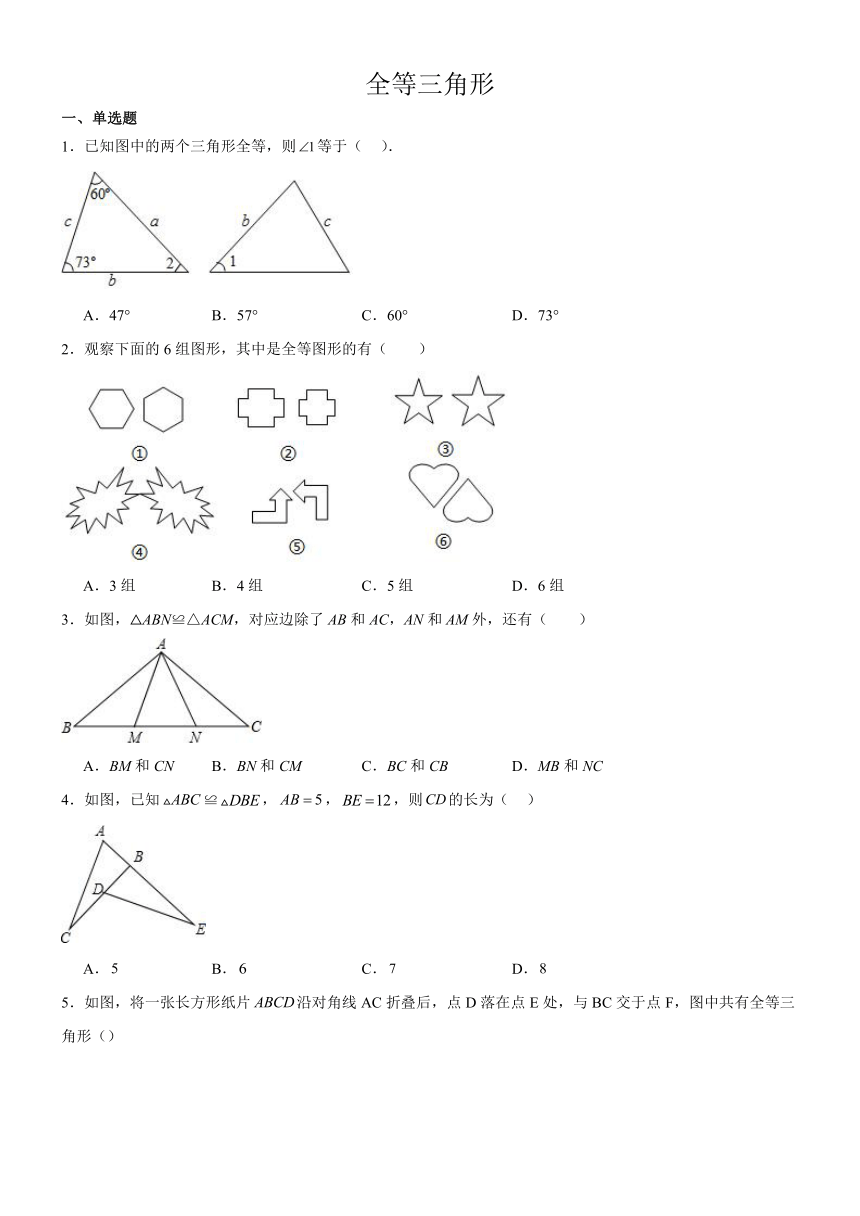 | |
| 格式 | docx | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 21:58:43 | ||
图片预览


文档简介
全等三角形
一、单选题
1.已知图中的两个三角形全等,则等于( ).
A.47° B.57° C.60° D.73°
2.观察下面的6组图形,其中是全等图形的有( )
A.3组 B.4组 C.5组 D.6组
3.如图,△ABN≌△ACM,对应边除了AB和AC,AN和AM外,还有( )
A.BM和CN B.BN和CM C.BC和CB D.MB和NC
4.如图,已知≌,,,则的长为( )
A. B. C. D.
5.如图,将一张长方形纸片沿对角线AC折叠后,点D落在点E处,与BC交于点F,图中共有全等三角形()
A.2对 B.3对 C.4对 D.5对
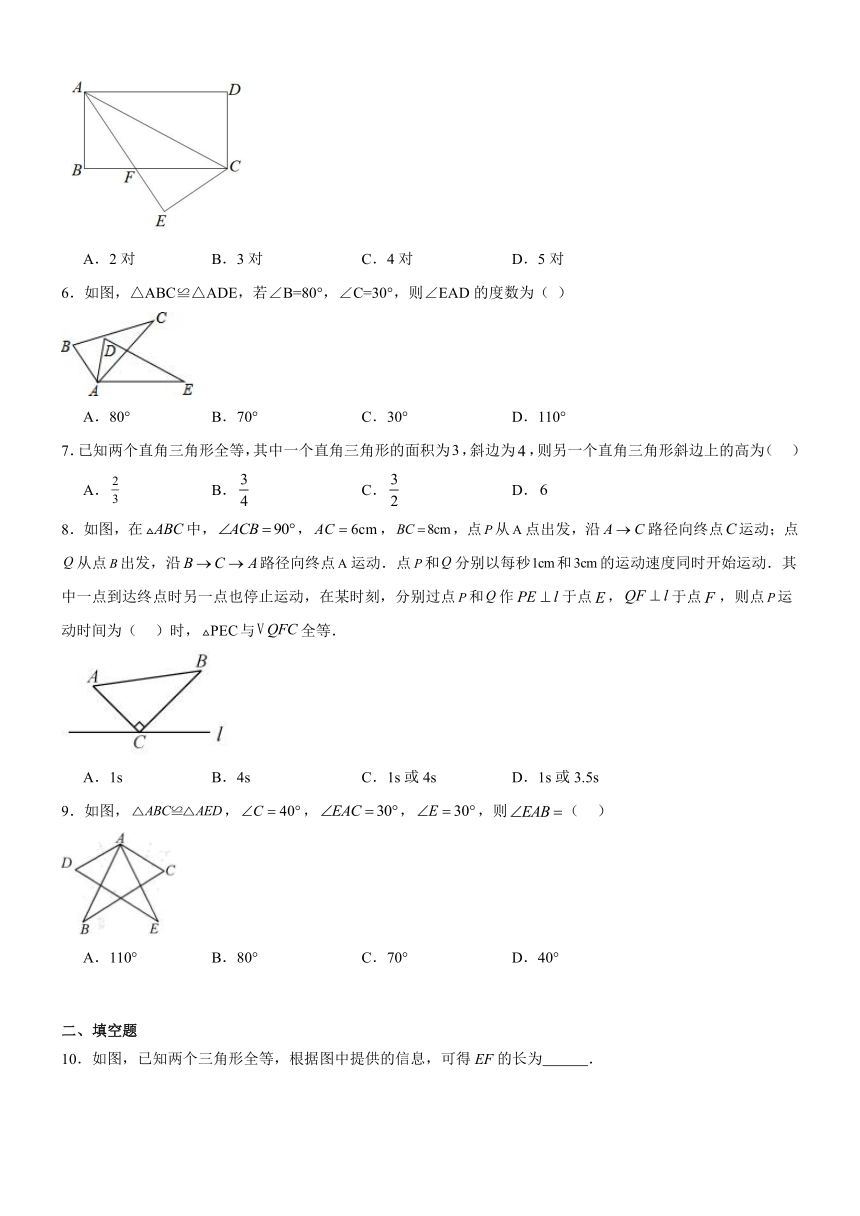
6.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
A.80° B.70° C.30° D.110°
7.已知两个直角三角形全等,其中一个直角三角形的面积为,斜边为,则另一个直角三角形斜边上的高为( )
A. B. C. D.
8.如图,在中,,,,点从点出发,沿路径向终点运动;点从点出发,沿路径向终点运动.点和分别以每秒和的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点和作于点,于点,则点运动时间为( )时,与全等.
A.1s B.4s C.1s或4s D.1s或3.5s
9.如图,,,,,则( )
A.110° B.80° C.70° D.40°
二、填空题
10.如图,已知两个三角形全等,根据图中提供的信息,可得EF的长为 .
11.已知(A、B分别对应 D、E),若BC=10cm,AB=5cm,则EF为 cm
12.如图所示,点A、B、C、D在同一条直线上,△ACF≌△DBE,AD=10cm,BC=6cm,则AB的长为 cm.
13.在如图所示的3×3正方形网格中, 度.
14.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片 即可
15.如图,ABC中,∠ACB=90°,AC=6cm,BC=8cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2cm/s和3cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t秒,则当t= 秒时,PEC与QFC全等.
三、解答题
16.知识重现:“能够完全重合的两个图形叫做全等形.”
理解应用:我们可以把4×4网格图形划分为两个全等图形.
范例:如图1和图2是两种不同的划分方法,其中图3与图1视为同一种划分方法.
请你再提供四种与上面不同的划分方法,分别在图4中画出来.
17.如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
18.如图,,且,,,求和的度数.
19.如图,,,,,C为AD的中点.
(1)求AE的长;
(2)求的度数.
参考答案:
1.A
2.B
3.B
4.C
5.C
6.B
7.C
8.D
9.B
10.20
11.10
12.2.
13.
14.②
15.2或或6
17.(1)24;(2)50
18.,
19.(1);
(2)
一、单选题
1.已知图中的两个三角形全等,则等于( ).
A.47° B.57° C.60° D.73°
2.观察下面的6组图形,其中是全等图形的有( )
A.3组 B.4组 C.5组 D.6组
3.如图,△ABN≌△ACM,对应边除了AB和AC,AN和AM外,还有( )
A.BM和CN B.BN和CM C.BC和CB D.MB和NC
4.如图,已知≌,,,则的长为( )
A. B. C. D.
5.如图,将一张长方形纸片沿对角线AC折叠后,点D落在点E处,与BC交于点F,图中共有全等三角形()
A.2对 B.3对 C.4对 D.5对
6.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
A.80° B.70° C.30° D.110°
7.已知两个直角三角形全等,其中一个直角三角形的面积为,斜边为,则另一个直角三角形斜边上的高为( )
A. B. C. D.
8.如图,在中,,,,点从点出发,沿路径向终点运动;点从点出发,沿路径向终点运动.点和分别以每秒和的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点和作于点,于点,则点运动时间为( )时,与全等.
A.1s B.4s C.1s或4s D.1s或3.5s
9.如图,,,,,则( )
A.110° B.80° C.70° D.40°
二、填空题
10.如图,已知两个三角形全等,根据图中提供的信息,可得EF的长为 .
11.已知(A、B分别对应 D、E),若BC=10cm,AB=5cm,则EF为 cm
12.如图所示,点A、B、C、D在同一条直线上,△ACF≌△DBE,AD=10cm,BC=6cm,则AB的长为 cm.
13.在如图所示的3×3正方形网格中, 度.
14.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片 即可
15.如图,ABC中,∠ACB=90°,AC=6cm,BC=8cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2cm/s和3cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t秒,则当t= 秒时,PEC与QFC全等.
三、解答题
16.知识重现:“能够完全重合的两个图形叫做全等形.”
理解应用:我们可以把4×4网格图形划分为两个全等图形.
范例:如图1和图2是两种不同的划分方法,其中图3与图1视为同一种划分方法.
请你再提供四种与上面不同的划分方法,分别在图4中画出来.
17.如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
18.如图,,且,,,求和的度数.
19.如图,,,,,C为AD的中点.
(1)求AE的长;
(2)求的度数.
参考答案:
1.A
2.B
3.B
4.C
5.C
6.B
7.C
8.D
9.B
10.20
11.10
12.2.
13.
14.②
15.2或或6
17.(1)24;(2)50
18.,
19.(1);
(2)
