华师大版数学八年级上册 13.5.3角平分线 课件(共23张PPT)
文档属性
| 名称 | 华师大版数学八年级上册 13.5.3角平分线 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 22:29:35 | ||
图片预览








文档简介
(共23张PPT)
第13章 全等三角形
13.5 逆命题与逆定理
第3课时 角平分线
引入
通过上节课我们知道,往往性质定理与其相应的判定定理互为逆定理.这节课我们将探究角平分线的性质定理及其逆定理——角平分线的判定定理.
探究新知
思考
(一)角平分线的性质定理
我们知道角平分线上的点到这个角的两边的距离相等,角平分线的这条性质是怎样得到的呢?
证明
A
E
B
D
O
P
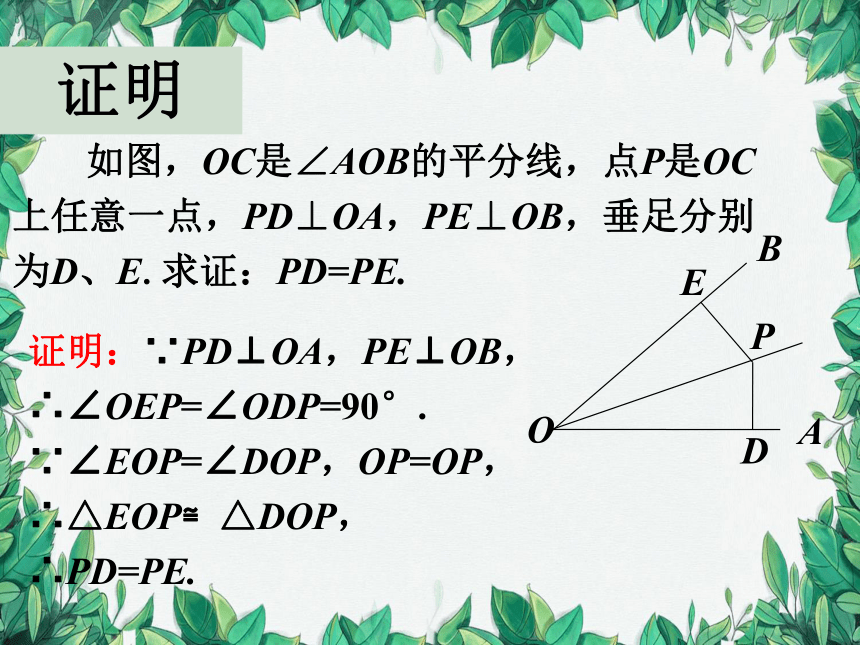
如图,OC是∠AOB的平分线,点P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D、E.求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠OEP=∠ODP=90°.
∵∠EOP=∠DOP,OP=OP,
∴△EOP≌△DOP,
∴PD=PE.
小结
定理:角平分线上的点到这个角的两边的距离相等.
思考
(二)角平分线的判定定理
角平分线性质定理的逆命题:到一个角的两边距离相等的点,在这个角的平分线上.这个命题是否是真命题呢?
证明
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
A
E
B
D
O
Q
证明:∵QD⊥OA,QE⊥OB,
∴∠OEQ=∠ODQ=90°.
∵QD=QE,OQ=OQ,
∴△EOQ≌△DOQ,
∴∠AOQ=∠BOQ.
故点Q在∠AOB的平分线上.
小结
定理:到一个角的两边距离相等的点,在这个角的平分线上.
思考
(三)三角形三条角平分线交于一点
已知:如图所示,AD、BE分别是△ABC中∠BAC与∠ABC的平分线,AD、BE相交于O.求证:∠ACB的平分线过点O.
A
B
C
D
E
O
证明:连接CO,延长CO交AB于F,过点O作OH⊥AC于H, OG⊥BC于G, OI⊥AB于I.
∵AD是∠BAC的平分线且O在AD上,
∴OH=OI.
∵ BE是∠ABC的平分线且O在BE上,
∴OG=OI,∴OH=OG.
又∵ OH⊥AC, OG⊥BC,
∴FC是∠ACB的平分线.
∴△ABC的三条内角平分线相交于一点O.
A
B
C
D
E
F
O
G
H
I
随堂练习
练习
1.如图,在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.
A
B
O
l
P
练习
2.如图,△ABC的外角∠CBD和∠BCE的平分线相交于一点F.求证:点F在∠DAE的平分线上.
A
B
D
C
E
F
证明
证明:
过F作FG⊥AD于G,FH⊥AE于H,FI⊥BC于I.
∵F是∠CBD和∠BCE平分线上的点,
∴FG=FI,FI=FH,
∴FG=FH.
又∵AF=AF,∠AGF=∠AHF=90°,
∴△AFG≌△AFH,
∴∠HAF= ∠GAF,
∴点F在∠DAE的平分线上.
A
B
D
C
E
F
G
H
I
课时总结
小结
要会证明角平分线的性质定理与判定定理,并会应用这个定理.
会证明三角形三条角平分线相交于一点,并会运用这个定理.
布置作业
作业
1.课本第99页习题13.5第4题.
作业
2.备选习题
(1)如图所示,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于点D,若CD=n,AB=m,则△ABD的面积是 ( )
C
B
A
D
作业
2.备选习题
(2)如图所示,FD⊥AM于D, FE⊥BM于E,下列能够证明△DMF≌△EMF的条件的个数是 ( )
A
M
D
E
F
B
① MF是∠AMB的平分线;
② DE=EF; ③ DM=EM;
④ ∠MFD=∠MFE.
A.1个 B.2个
C.3个 D.4个
作业
(3)如图,AB//CD,CE平分∠ACD交AB于E,∠A=118°,则∠AEC= 度.
2.备选习题
A
B
C
D
E
第13章 全等三角形
13.5 逆命题与逆定理
第3课时 角平分线
引入
通过上节课我们知道,往往性质定理与其相应的判定定理互为逆定理.这节课我们将探究角平分线的性质定理及其逆定理——角平分线的判定定理.
探究新知
思考
(一)角平分线的性质定理
我们知道角平分线上的点到这个角的两边的距离相等,角平分线的这条性质是怎样得到的呢?
证明
A
E
B
D
O
P
如图,OC是∠AOB的平分线,点P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D、E.求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠OEP=∠ODP=90°.
∵∠EOP=∠DOP,OP=OP,
∴△EOP≌△DOP,
∴PD=PE.
小结
定理:角平分线上的点到这个角的两边的距离相等.
思考
(二)角平分线的判定定理
角平分线性质定理的逆命题:到一个角的两边距离相等的点,在这个角的平分线上.这个命题是否是真命题呢?
证明
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
A
E
B
D
O
Q
证明:∵QD⊥OA,QE⊥OB,
∴∠OEQ=∠ODQ=90°.
∵QD=QE,OQ=OQ,
∴△EOQ≌△DOQ,
∴∠AOQ=∠BOQ.
故点Q在∠AOB的平分线上.
小结
定理:到一个角的两边距离相等的点,在这个角的平分线上.
思考
(三)三角形三条角平分线交于一点
已知:如图所示,AD、BE分别是△ABC中∠BAC与∠ABC的平分线,AD、BE相交于O.求证:∠ACB的平分线过点O.
A
B
C
D
E
O
证明:连接CO,延长CO交AB于F,过点O作OH⊥AC于H, OG⊥BC于G, OI⊥AB于I.
∵AD是∠BAC的平分线且O在AD上,
∴OH=OI.
∵ BE是∠ABC的平分线且O在BE上,
∴OG=OI,∴OH=OG.
又∵ OH⊥AC, OG⊥BC,
∴FC是∠ACB的平分线.
∴△ABC的三条内角平分线相交于一点O.
A
B
C
D
E
F
O
G
H
I
随堂练习
练习
1.如图,在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.
A
B
O
l
P
练习
2.如图,△ABC的外角∠CBD和∠BCE的平分线相交于一点F.求证:点F在∠DAE的平分线上.
A
B
D
C
E
F
证明
证明:
过F作FG⊥AD于G,FH⊥AE于H,FI⊥BC于I.
∵F是∠CBD和∠BCE平分线上的点,
∴FG=FI,FI=FH,
∴FG=FH.
又∵AF=AF,∠AGF=∠AHF=90°,
∴△AFG≌△AFH,
∴∠HAF= ∠GAF,
∴点F在∠DAE的平分线上.
A
B
D
C
E
F
G
H
I
课时总结
小结
要会证明角平分线的性质定理与判定定理,并会应用这个定理.
会证明三角形三条角平分线相交于一点,并会运用这个定理.
布置作业
作业
1.课本第99页习题13.5第4题.
作业
2.备选习题
(1)如图所示,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于点D,若CD=n,AB=m,则△ABD的面积是 ( )
C
B
A
D
作业
2.备选习题
(2)如图所示,FD⊥AM于D, FE⊥BM于E,下列能够证明△DMF≌△EMF的条件的个数是 ( )
A
M
D
E
F
B
① MF是∠AMB的平分线;
② DE=EF; ③ DM=EM;
④ ∠MFD=∠MFE.
A.1个 B.2个
C.3个 D.4个
作业
(3)如图,AB//CD,CE平分∠ACD交AB于E,∠A=118°,则∠AEC= 度.
2.备选习题
A
B
C
D
E
