沪科版数学九年级上册 23.1锐角的三角函数(第2课时)课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.1锐角的三角函数(第2课时)课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 305.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第2课时 锐角的三角函数(2)
问题导入
1.分别求出图中∠A,∠B的正切值.
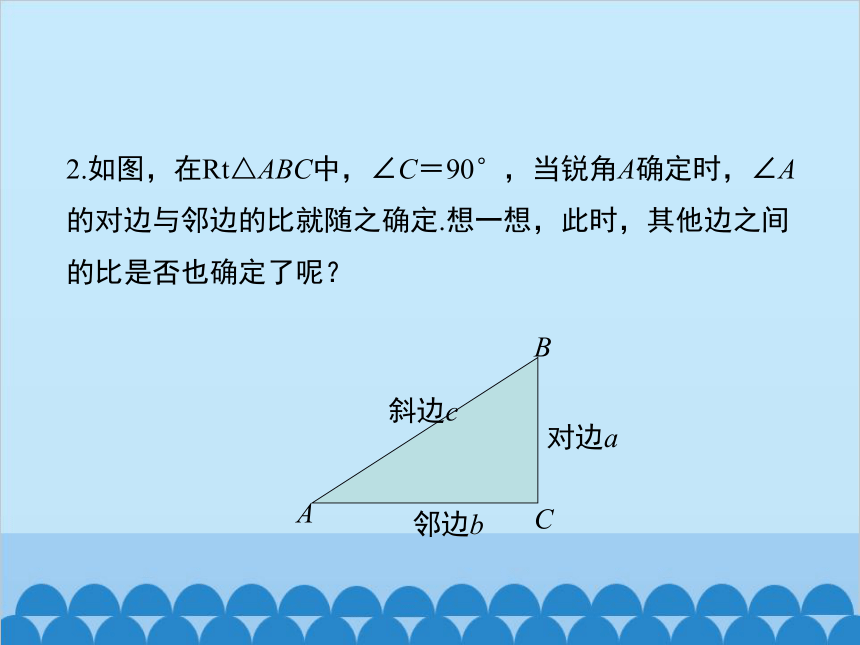
2.如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定.想一想,此时,其他边之间的比是否也确定了呢?
A
B
C
邻边b
对边a
斜边c
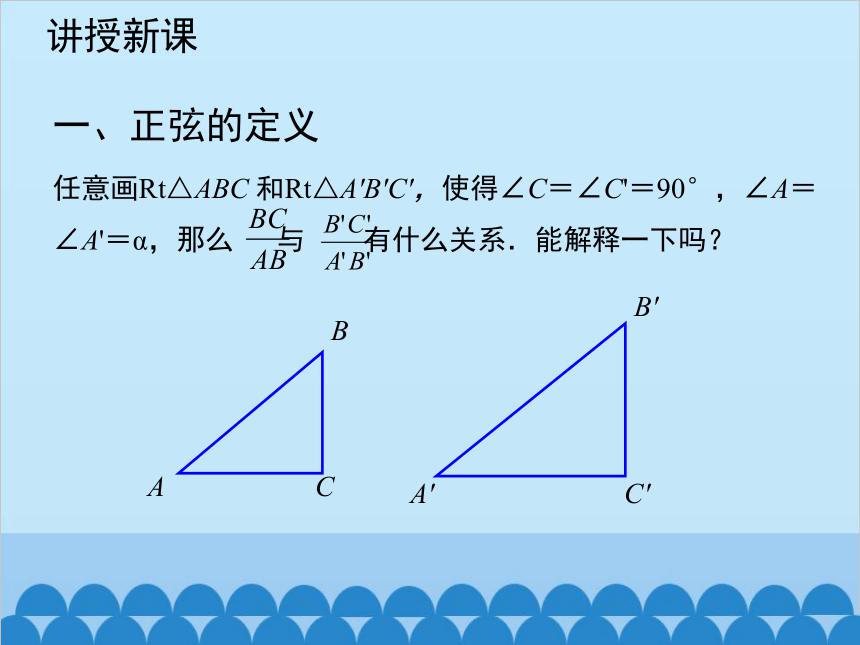
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A'
B'
C'
讲授新课
一、正弦的定义
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
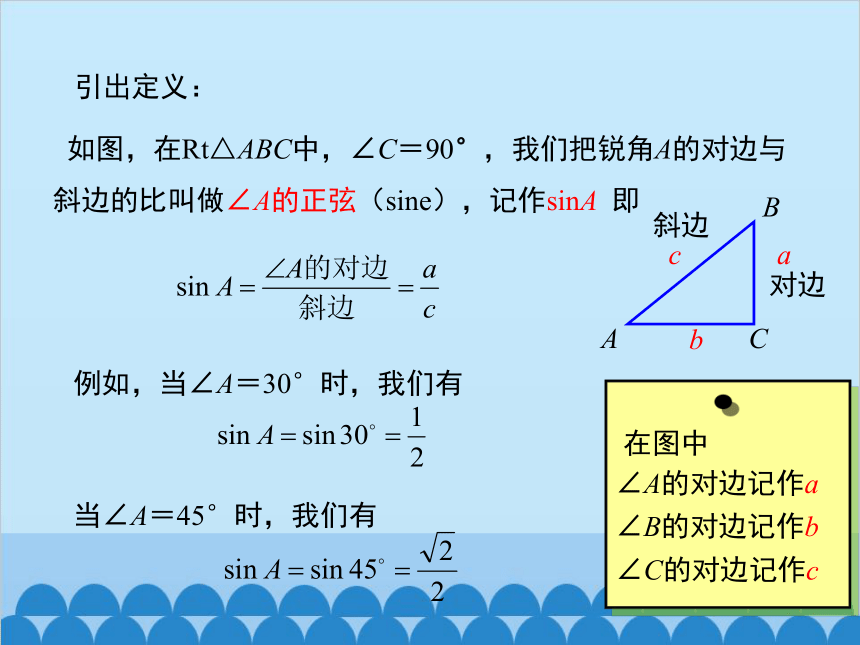
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA 即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
引出定义:
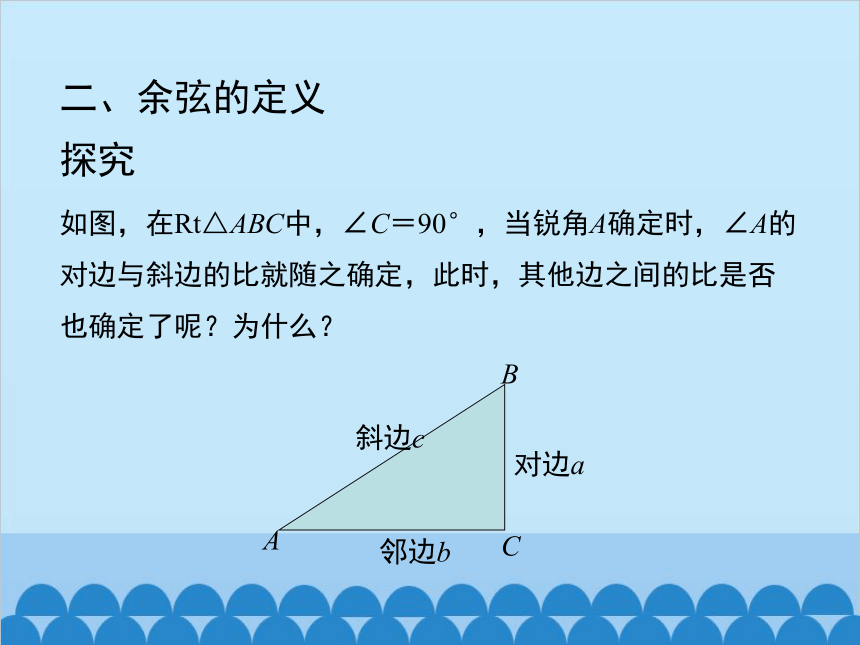
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
邻边b
对边a
斜边c
探究
二、余弦的定义
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠B=∠B'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A'
B'
C'
在图中,由于∠C=∠C'=90°,∠B=∠B'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角B的度数一定时,不管三角形的大小如何,∠B的邻边与斜边的比也是一个固定值.
当锐角B的大小确定时,我们把∠B的邻边与斜边的比叫做∠B的余弦(cosine),记作cosB,即
引出定义:
归纳总结
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,图中sinB可由哪两条线段比求得?
D
C
B
A
解:在Rt△ABC中,
在Rt△BCD中,
因为∠B=∠ACD,所以
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值.
课堂练习
2. 如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
解:∵
又∵
A
B
C
6
10
3. 如图,在Rt△ABC中,∠C=90°,cosA= ,求sinA、tanA的值.
解:∵
A
B
C
设AC=15k,则AB=17k
所以
∴
4.如图,∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
5. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.
A
B
C
8
解:∵
在Rt△ABC中
=
a
b
tanA=
课堂小结
定义中应该注意的几个问题:
1.sinA、cosA、tanA是在直角三角形中定义的,∠A是锐 角(注意数形结合,构造直角三角形).
2.sinA、 cosA、tanA是一个比值(数值).
3.sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
第2课时 锐角的三角函数(2)
问题导入
1.分别求出图中∠A,∠B的正切值.
2.如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定.想一想,此时,其他边之间的比是否也确定了呢?
A
B
C
邻边b
对边a
斜边c
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A'
B'
C'
讲授新课
一、正弦的定义
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA 即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
引出定义:
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
邻边b
对边a
斜边c
探究
二、余弦的定义
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠B=∠B'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A'
B'
C'
在图中,由于∠C=∠C'=90°,∠B=∠B'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角B的度数一定时,不管三角形的大小如何,∠B的邻边与斜边的比也是一个固定值.
当锐角B的大小确定时,我们把∠B的邻边与斜边的比叫做∠B的余弦(cosine),记作cosB,即
引出定义:
归纳总结
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,图中sinB可由哪两条线段比求得?
D
C
B
A
解:在Rt△ABC中,
在Rt△BCD中,
因为∠B=∠ACD,所以
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值.
课堂练习
2. 如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
解:∵
又∵
A
B
C
6
10
3. 如图,在Rt△ABC中,∠C=90°,cosA= ,求sinA、tanA的值.
解:∵
A
B
C
设AC=15k,则AB=17k
所以
∴
4.如图,∠ACB=90°,CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
5. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.
A
B
C
8
解:∵
在Rt△ABC中
=
a
b
tanA=
课堂小结
定义中应该注意的几个问题:
1.sinA、cosA、tanA是在直角三角形中定义的,∠A是锐 角(注意数形结合,构造直角三角形).
2.sinA、 cosA、tanA是一个比值(数值).
3.sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
