12.1 幂的运算(第1课时)教学课件(共24张PPT)八年级数学上册(华东师大版)
文档属性
| 名称 | 12.1 幂的运算(第1课时)教学课件(共24张PPT)八年级数学上册(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 21:58:32 | ||
图片预览








文档简介
(共24张PPT)
12.1 幂的运算
第1课时 同底数幂的乘法
数学(华东师大版)
八年级 上册
第12章 整式的乘除
学习目标
1.掌握同底数幂的乘法运算法则;
2.学会利用同底数幂的乘法运算法则来计算;
导入新课
某地区在退耕还林期间,将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积,你知道下面的等式蕴含着什么样的运算法则吗?
m
n
b
am
bm
an
bn
(m+n)(a+b) =ma+mb+na+nb
a
导入新课
“盘古开天辟地”的故事:公元前一百万年,没有天没有地,整个宇宙是混浊的一团,突然间窜出来一个巨人,他的名字叫盘古,他手握一把巨斧,用力一劈,把混沌的宇宙劈成两半,上面是天,下面是地,从此宇宙有了天地之分,盘古完成了这样一个壮举,累死了,他的左眼变成了太阳,右眼变成了月亮,毛发变成了森林和草原,骨头变成了高山和高原,肌肉变成了平原与谷地,血液变成了河流.
讲授新课
知识点一 同底数幂的乘法
盘古的左眼变成了太阳,那么,太阳离我们多远呢?你可以计算一下,太阳到地球的距离是多少?
光的速度为3×105千米/秒,太阳光照射到地球大约需要5×102秒,你能计算出地球距离太阳大约有多远呢?
3×105×5×102=15×105×102=15×?
105×102
思考探究
讲授新课
105×102
105×102
=10×10×10×10×10×10×10
=107
讲授新课
探究新知
试一试
根据幂的意义填空:
(1)23×24=
(2×2×2)×(2×2×2×2)
=2×2×2×2×2×2×2
=27
=3+4
3
4
3个2
4个2
7个2
讲授新课
(3)(-3)3×(-3)4
(2)53×54=
(5×5×5)×(5×5×5×5)
=5×5×5×5×5×5×5
=57
=3+4
3
4
3个5
4个5
7个5
=(-3)×(-3)×(-3)×(-3)×(-3)×(-3)×(-3)
=[(-3)×(-3)×(-3)]×[(-3)×(-3)×(-3)×(-3)]
=(-3)7
讲授新课
(5)a3·a4=
(a · a · a)(a · a · a · a)
=a · a · a · a · a · a · a
=a7
=3+4
3
4
3个a
4个a
7个a
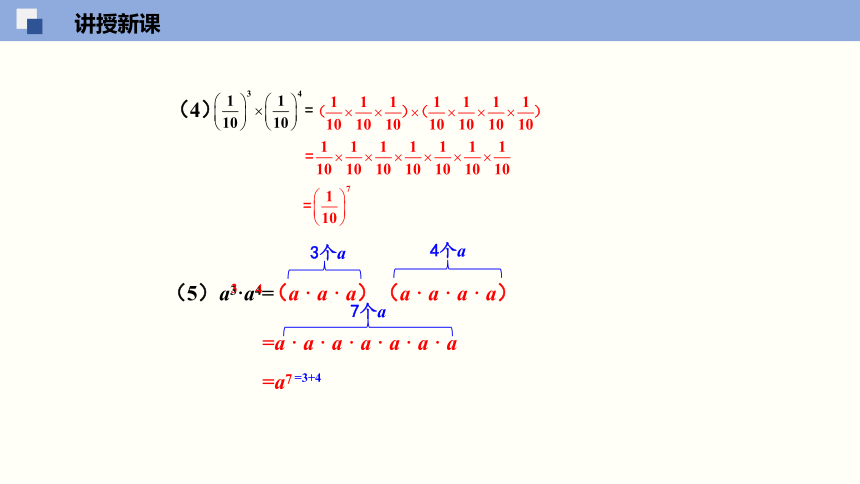
(4)
讲授新课
am·an=(a · a · a· … · a)(a · a · a· … · a)
=a · a · a· … · a
=am+n
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
可得
m个a
n个a
(m+n)个a
讲授新课
典例精析
【例1】若,则m的值为( )
A.1 B.2 C.3 D.4
【详解】解:∵,
∴,
∴4m+2=10,
∴解得:m=2,
故选B.
讲授新课
练一练
1.若2×4×8×16=,则m= .
【详解】解:∵2×4×8×16= ,
∴2×22×23×24=2m,
∴210=2m,
∴m=10;
故答案为:10.
讲授新课
2.计算下列各式,结果用幂的形式表示.
(1);
(2);
(3).
【详解】(1)解:原式=a3·a5
=a8;
(2)解:原式=(y-x)2(y-x)3
=(y-x)5;
(3)解:原式=(x-2y)2+m-1+m+2
=a2m+3.
当堂检测
1.计算所得结果是( )
A.22022 B.-22022 C.22023 D.-22023
【详解】解:原式=
=[1+(-2)]
=-22022
故选:B
当堂检测
2.若x+2y-4=0,则2x·4y的值等于:( )
A.4 B.6 C.8 D.16
【详解】解:∵x+2y-4=0,
∴x+2y=4,
∴2x·4y=2x·2×2y=2x+2y=24=16,
故选.
当堂检测
3.已知若3·32m·33m=326,则m等于( )
A.3 B.4 C.5 D.6
【详解】解:∵3·32m·33m=326,
∴32m+3m+1=326,
∴2m+3m+1=26,
解得m=5,
故选C.
当堂检测
4.-2m2·3m3= .
【详解】解:原式=-6m5,
故答案为:-6m5.
5.若xn-1·xn+5=x10,则n= .
【详解】解:xn-1·xn+5=x10,
n-1+n+5=10,
则n=3.
故答案为:3.
当堂检测
6.计算:(a-b)2(b-a)3(a-b)4= .
【详解】解:原式=(b-a)3(b-a)3(b-a)4=(b-a)9,
故答案为:(b-a)9.
当堂检测
7.计算下列各式,结果用幂的形式表示:
(1)25×26;
(2)a·a2·a3;
(3)(a+b)2·(a+b)4;
(4)(x-y)2(x-y)3(x-y)5.
【详解】(1)解:原式=25+6=211;
(2)解:原式=a1+2+3=a6;
(3)解:原式=(a+b)2+4=(a+b)6;
(4)解:原式=(x-y)2+3+5=(x-y)10
当堂检测
8.如果xm-n·x2n+1=x11,且ym-1·y4-n=y7,求m,n的值.
【详解】解:∵xm-n·x2n+1=x11,且ym-1·y4-n=y7,
∴,
解得,
即m=7,n=3.
当堂检测
9.如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)=__________,(4,256)=_________,(2,2)=________
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
【详解】(1)解:∵33=27,
∴(3,27)=3,
∵44=256,∴(4,256)=4,
∵21=2,∴(2,2)=1,
故答案为:3,4,1;
当堂检测
(2)证明:(3,5)=a,(3,6)=b,(3,30)=c,
3a=5,3b=6,3c=30,
3a×3b=30,
3a×3b=3c,
∴3a+b=3c
∴a+b=c.
课堂小结
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法
公式:
文字描述:
谢 谢~
12.1 幂的运算
第1课时 同底数幂的乘法
数学(华东师大版)
八年级 上册
第12章 整式的乘除
学习目标
1.掌握同底数幂的乘法运算法则;
2.学会利用同底数幂的乘法运算法则来计算;
导入新课
某地区在退耕还林期间,将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积,你知道下面的等式蕴含着什么样的运算法则吗?
m
n
b
am
bm
an
bn
(m+n)(a+b) =ma+mb+na+nb
a
导入新课
“盘古开天辟地”的故事:公元前一百万年,没有天没有地,整个宇宙是混浊的一团,突然间窜出来一个巨人,他的名字叫盘古,他手握一把巨斧,用力一劈,把混沌的宇宙劈成两半,上面是天,下面是地,从此宇宙有了天地之分,盘古完成了这样一个壮举,累死了,他的左眼变成了太阳,右眼变成了月亮,毛发变成了森林和草原,骨头变成了高山和高原,肌肉变成了平原与谷地,血液变成了河流.
讲授新课
知识点一 同底数幂的乘法
盘古的左眼变成了太阳,那么,太阳离我们多远呢?你可以计算一下,太阳到地球的距离是多少?
光的速度为3×105千米/秒,太阳光照射到地球大约需要5×102秒,你能计算出地球距离太阳大约有多远呢?
3×105×5×102=15×105×102=15×?
105×102
思考探究
讲授新课
105×102
105×102
=10×10×10×10×10×10×10
=107
讲授新课
探究新知
试一试
根据幂的意义填空:
(1)23×24=
(2×2×2)×(2×2×2×2)
=2×2×2×2×2×2×2
=27
=3+4
3
4
3个2
4个2
7个2
讲授新课
(3)(-3)3×(-3)4
(2)53×54=
(5×5×5)×(5×5×5×5)
=5×5×5×5×5×5×5
=57
=3+4
3
4
3个5
4个5
7个5
=(-3)×(-3)×(-3)×(-3)×(-3)×(-3)×(-3)
=[(-3)×(-3)×(-3)]×[(-3)×(-3)×(-3)×(-3)]
=(-3)7
讲授新课
(5)a3·a4=
(a · a · a)(a · a · a · a)
=a · a · a · a · a · a · a
=a7
=3+4
3
4
3个a
4个a
7个a
(4)
讲授新课
am·an=(a · a · a· … · a)(a · a · a· … · a)
=a · a · a· … · a
=am+n
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
可得
m个a
n个a
(m+n)个a
讲授新课
典例精析
【例1】若,则m的值为( )
A.1 B.2 C.3 D.4
【详解】解:∵,
∴,
∴4m+2=10,
∴解得:m=2,
故选B.
讲授新课
练一练
1.若2×4×8×16=,则m= .
【详解】解:∵2×4×8×16= ,
∴2×22×23×24=2m,
∴210=2m,
∴m=10;
故答案为:10.
讲授新课
2.计算下列各式,结果用幂的形式表示.
(1);
(2);
(3).
【详解】(1)解:原式=a3·a5
=a8;
(2)解:原式=(y-x)2(y-x)3
=(y-x)5;
(3)解:原式=(x-2y)2+m-1+m+2
=a2m+3.
当堂检测
1.计算所得结果是( )
A.22022 B.-22022 C.22023 D.-22023
【详解】解:原式=
=[1+(-2)]
=-22022
故选:B
当堂检测
2.若x+2y-4=0,则2x·4y的值等于:( )
A.4 B.6 C.8 D.16
【详解】解:∵x+2y-4=0,
∴x+2y=4,
∴2x·4y=2x·2×2y=2x+2y=24=16,
故选.
当堂检测
3.已知若3·32m·33m=326,则m等于( )
A.3 B.4 C.5 D.6
【详解】解:∵3·32m·33m=326,
∴32m+3m+1=326,
∴2m+3m+1=26,
解得m=5,
故选C.
当堂检测
4.-2m2·3m3= .
【详解】解:原式=-6m5,
故答案为:-6m5.
5.若xn-1·xn+5=x10,则n= .
【详解】解:xn-1·xn+5=x10,
n-1+n+5=10,
则n=3.
故答案为:3.
当堂检测
6.计算:(a-b)2(b-a)3(a-b)4= .
【详解】解:原式=(b-a)3(b-a)3(b-a)4=(b-a)9,
故答案为:(b-a)9.
当堂检测
7.计算下列各式,结果用幂的形式表示:
(1)25×26;
(2)a·a2·a3;
(3)(a+b)2·(a+b)4;
(4)(x-y)2(x-y)3(x-y)5.
【详解】(1)解:原式=25+6=211;
(2)解:原式=a1+2+3=a6;
(3)解:原式=(a+b)2+4=(a+b)6;
(4)解:原式=(x-y)2+3+5=(x-y)10
当堂检测
8.如果xm-n·x2n+1=x11,且ym-1·y4-n=y7,求m,n的值.
【详解】解:∵xm-n·x2n+1=x11,且ym-1·y4-n=y7,
∴,
解得,
即m=7,n=3.
当堂检测
9.如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)=__________,(4,256)=_________,(2,2)=________
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
【详解】(1)解:∵33=27,
∴(3,27)=3,
∵44=256,∴(4,256)=4,
∵21=2,∴(2,2)=1,
故答案为:3,4,1;
当堂检测
(2)证明:(3,5)=a,(3,6)=b,(3,30)=c,
3a=5,3b=6,3c=30,
3a×3b=30,
3a×3b=3c,
∴3a+b=3c
∴a+b=c.
课堂小结
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法
公式:
文字描述:
谢 谢~
