2.1.2有理数 课件(共30张PPT)七年级数学上册(华东师大版)
文档属性
| 名称 | 2.1.2有理数 课件(共30张PPT)七年级数学上册(华东师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 22:04:36 | ||
图片预览










文档简介
(共30张PPT)
2.1 有理数
第2课时 有理数
数学(华东师大版)
七年级 上册
第2章 有理数
学习目标
1.掌握有理数的概念和意义;
2.学会根据不同的标准对有理数进行分类,培养学生的分类能力;
温故知新
像﹣2,﹣2.5,﹣237,﹣0.7这样的数叫做负数.
像13,3.5,500、1.2等这样的数是正数.
负数比0小,负数前面的“﹣”号不可省略.
有时为了突出数的符号,常在正数前面加上“+”,如+6, +8,+8844···,有时也可省略“+”号.
0既不是正数,也不是负数,0是正数和负数的分界.
导入新课
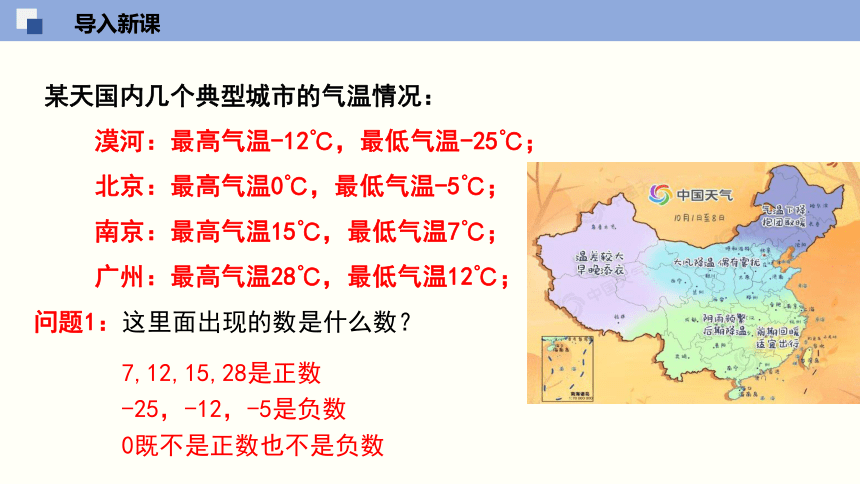
某天国内几个典型城市的气温情况:
漠河:最高气温-12℃,最低气温-25℃;
北京:最高气温0℃,最低气温-5℃;
南京:最高气温15℃,最低气温7℃;
广州:最高气温28℃,最低气温12℃;
问题1:这里面出现的数是什么数?
7,12,15,28是正数
-25,-12,-5是负数
0既不是正数也不是负数
讲授新课
知识点一 有理数的概念
1.目前我们所学的小数有哪几类?
2. 0.1,-0.5,5.32,-150.25, 能化成分数吗?
有限小数,无限小数(无限循环小数和无限不循环小数)
这些能化为分数的小数,都看作为分数。
讲授新课
我们把1,2,3,4,…称为正整数;
-1,-2,-3,-4,…称为负整数;
, , ,4.5,…称为正分数;
, , ,-4.5,…称为负分数.
讲授新课
正整数、零和负整数统称整数;
整数和分数统称有理数.
正分数和负分数统称分数.
正整数、零和负整数统称整数。
整数和分数统称为有理数。
正分数和负分数统称分数。
有理数的概念
讲授新课
典例精析
【例1】在,π,4,,0,-0.3中,表示有理数的有( )
A.3个 B.4个 C.5个 D.6个
【详解】解:在 ,π,4, ,0,-0.3中,
表示有理数的有:,4,,0,-0.3,共有5个,
故选:C.
讲授新课
练一练
1.在,-4.01,5,,0中有理数有 个
【详解】解: ,-4.01,5, ,0中
是有理数的为:,-4.01,5,0,共4个;
故答案为:4.
讲授新课
2.把下列各数填在相应的表示集合的大括号里:4,0.5,,10%,-5,-3.14,0,,+2022,
(1)正整数集合{ };
(2)分数集合{ };
(3)负分数集合{ };
(4)整数集合{ }.
【详解】(1)解:正整数集合为:4,+2022;
(2)解:分数集合为:0.5,,10%,-3.14,;
(3)解:负分数集合为:,-3.14;
(4)解:整数集合为:4,-5,0,+2022
讲授新课
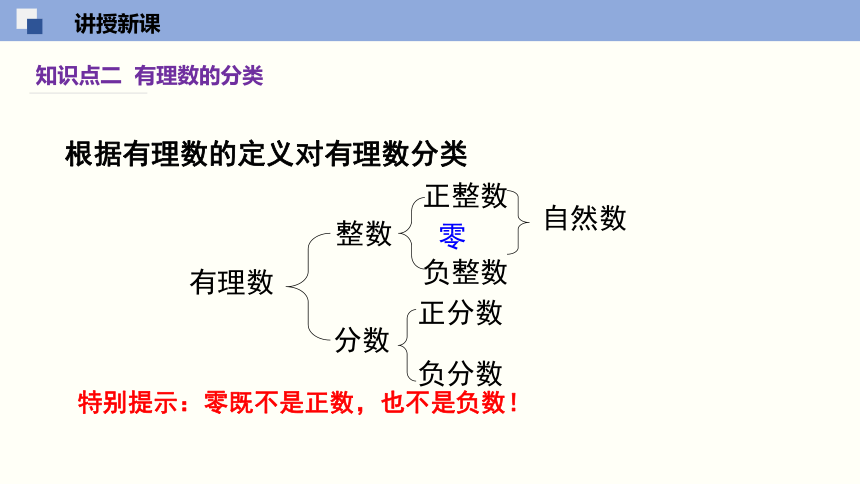
知识点二 有理数的分类
特别提示:零既不是正数,也不是负数!
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
根据有理数的定义对有理数分类
讲授新课
有理数分类的几点注意:
1.如 能约分成整数的数_____(填“能”或“不能”)算做分数;
不能
2.无限不循环小数不是有理数,如π;(无理数)
3.整数中除了正整数和负整数,还有___。
0
有理数还有其他的分类方法吗?
讲授新课
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数按符号(正、负)分类如下:
注意: ①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数。
讲授新课
典例精析
【例2】下列说法中错误的是( )
A.正有理数、零、负有理数统称为有理数
B.正数与零统称为非负数
C.非正数都比零小 D.正整数和正分数组成正有理数
【详解】正有理数、零、负有理数统称为有理数,
选项A不符合题意;
正数与零统称为非负数,选项B不符合题意;
非正数都小于或等于0,选项C符合题意;
正整数和正分数组成正有理数,选项D不符合题意.
故选C.
讲授新课
练一练
1.给出下列各数:4.443,0,3.1159,-1000,,其中分数的个数是m,非正数的个数是n,则m+n= .
【详解】解:∵4.443,3.1159, ,是分数,
∴m=3,
∵0,-1000,是非正数,
∴n=3,
∴m+n=3+3=6.
故答案为:6.
讲授新课
2.把下列各数填在相应的表示集合的大括号里:4,0.5,,10%,-5,-3.14,0,,+2022,
(1)正整数集合{ };
(2)分数集合{ };
(3)负分数集合{ };
(4)整数集合{ }.
【详解】(1)解:正整数集合为:4,+2022;
(2)解:分数集合为:0.5,,10%,-3.14,;
(3)解:负分数集合为:,-3.14;
(4)解:整数集合为:4,-5,0,+2022
讲授新课
知识点三 带“非”字的有理数
非负数是 ,
非正数是 ,
非负整数是 ,
非正整数是 .
零和正数
零和正整数
零和负数
零和负整数
1、零是______________________________;
2、零不是_____________________________;
正数, 不是负数, 也不是分数
自然数, 是整数, 是有理数
讲授新课
典例精析
【例3】在-15,,-0.23,0,7.6,2,,314%.这八个有理数中非负数有( )
A.4个 B.5个 C.6个 D.7个
【详解】解:在-15, ,-0.23,0,7.6,2, ,3.14%这八个数中,
非负数为,0,7.6,2,314%,有5个.
故选:B.
讲授新课
练一练
1.有理数2,+7.5,-0.03,-0.4,0,,10中,非负整数有 个.
【详解】解:有理数2,+7.5,-0.03,-0.4,0, ,10中,非负整数有2,0,10共3个,
故答案为:3.
当堂检测
1.下列各数中,是正分数的是( )
A. B.0 C.3 D.2.5
【详解】A、是负分数,此选项不符合题意,排除;
B、0既不是正数,也不是负数,此选项不符合题意,排除;
C、3是整数,此选项不符合题意,排除;
D、2.5是正分数,此选项符合题意;
故选:D.
当堂检测
2.在一组数-2,0.4,0,π,,,3.5151151115···(相邻的两个5之间依次多一个1)中,有理数的个数是( )
A.3 B.4 C.5 D.6
【详解】解:在实数-2,0.4,0,π, , ,3.5151151115···(相邻的两个5之间依次多一个1)中,有理数有-2,0.4,0,,,共5个.
故选:C.
当堂检测
3.下列说法①正整数和负整数统称整数②零既不是正数,也不是非负数③有理数除整数外,其余全是分数④正分数和负分数统称为分数.其中正确的有( )
A.0个 B.1个 C.2个 D.3
【详解】正整数、负整数和0统称整数,故①错误;
零是非负数,故②错误;
有理数除整数外,其余全是分数,故③正确;
正分数和负分数统称为分数,故④正确;
故选:C.
当堂检测
4.大于-4且小于3.2的所有整数的和等于 .
【详解】解:由题意得:大于-4而小于3.2的整数有:-3,-2,-1,0,1,2,3,
∴(-3)+(-2)+(-1)+0+1+2+3=0,
故答案为:0.
当堂检测
5.有理数-1.7,-17,0,,-1,,-0.001,2003中,负分数有 个.
【详解】解:负分数有:-1.7,,,-0.001,共4个,
故答案为:4.
当堂检测
6.在,,0,-1,0.4,π,2,-3,-6这些数中,有理数有m个,自然数有n个,分数有k个,则m-n-k的值为 .
【详解】∵ , ,0,-1,0.4,π,2,-3,-6,
∴有理数有m=8个,自然数有n=2个,分数有k=3个,
∴m-n-k=8-2-3=3,
故答案为:3.
当堂检测
7.把下列各数填入相应集合的括号内.
+6.5,,0.5,0,-3.2,13,-9,,-1,-3.6,
(1)正分数集合:{____________…};
(2)整数集合:{____________…};
(3)非负数集合:{____________…).
【详解】(1)解:根据正分数的定义,正分数有:+6.5,0.5,,
故答案为:+6.5,0.5, ;
(2)解:根据整数的定义,整数有:0,13,-9,-1,
故答案为:0,13,-9,-1;
(3)解:根据非负数的定义,非负数有:+6.5,0.5,0,13,,,
故答案为:+6.5,0.5,0,13, , .
当堂检测
8.“不是正数的数一定是负数,不是负教的数一定是正数”的说法对吗?为什么?
【详解】不对.因为0既不是正数也不是负数.
当堂检测
9.把下列各数按要求分类:5.2,0,,,+(-4),,-(-3),0.2555···,-0.030030003···.
(1)写出所有的分数;
(2)写出所有的非负整数;
(3)写出所有的有理数.
【详解】(1)分数集合:{5.2,,,0.2555……}.
(2)非负整数集合:{0,-(-3)}.
(3)有理数集合:{ 5.2,0,,+(-4),,-(-3),0.2555……}.
课堂小结
1.整数和分数统称为有理数;(目前我们学过的数中,只有π不是有理数)
2.有理数的分类
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
3.注意0的特殊性,在分类时千万不要遗漏0.
谢 谢~
2.1 有理数
第2课时 有理数
数学(华东师大版)
七年级 上册
第2章 有理数
学习目标
1.掌握有理数的概念和意义;
2.学会根据不同的标准对有理数进行分类,培养学生的分类能力;
温故知新
像﹣2,﹣2.5,﹣237,﹣0.7这样的数叫做负数.
像13,3.5,500、1.2等这样的数是正数.
负数比0小,负数前面的“﹣”号不可省略.
有时为了突出数的符号,常在正数前面加上“+”,如+6, +8,+8844···,有时也可省略“+”号.
0既不是正数,也不是负数,0是正数和负数的分界.
导入新课
某天国内几个典型城市的气温情况:
漠河:最高气温-12℃,最低气温-25℃;
北京:最高气温0℃,最低气温-5℃;
南京:最高气温15℃,最低气温7℃;
广州:最高气温28℃,最低气温12℃;
问题1:这里面出现的数是什么数?
7,12,15,28是正数
-25,-12,-5是负数
0既不是正数也不是负数
讲授新课
知识点一 有理数的概念
1.目前我们所学的小数有哪几类?
2. 0.1,-0.5,5.32,-150.25, 能化成分数吗?
有限小数,无限小数(无限循环小数和无限不循环小数)
这些能化为分数的小数,都看作为分数。
讲授新课
我们把1,2,3,4,…称为正整数;
-1,-2,-3,-4,…称为负整数;
, , ,4.5,…称为正分数;
, , ,-4.5,…称为负分数.
讲授新课
正整数、零和负整数统称整数;
整数和分数统称有理数.
正分数和负分数统称分数.
正整数、零和负整数统称整数。
整数和分数统称为有理数。
正分数和负分数统称分数。
有理数的概念
讲授新课
典例精析
【例1】在,π,4,,0,-0.3中,表示有理数的有( )
A.3个 B.4个 C.5个 D.6个
【详解】解:在 ,π,4, ,0,-0.3中,
表示有理数的有:,4,,0,-0.3,共有5个,
故选:C.
讲授新课
练一练
1.在,-4.01,5,,0中有理数有 个
【详解】解: ,-4.01,5, ,0中
是有理数的为:,-4.01,5,0,共4个;
故答案为:4.
讲授新课
2.把下列各数填在相应的表示集合的大括号里:4,0.5,,10%,-5,-3.14,0,,+2022,
(1)正整数集合{ };
(2)分数集合{ };
(3)负分数集合{ };
(4)整数集合{ }.
【详解】(1)解:正整数集合为:4,+2022;
(2)解:分数集合为:0.5,,10%,-3.14,;
(3)解:负分数集合为:,-3.14;
(4)解:整数集合为:4,-5,0,+2022
讲授新课
知识点二 有理数的分类
特别提示:零既不是正数,也不是负数!
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
根据有理数的定义对有理数分类
讲授新课
有理数分类的几点注意:
1.如 能约分成整数的数_____(填“能”或“不能”)算做分数;
不能
2.无限不循环小数不是有理数,如π;(无理数)
3.整数中除了正整数和负整数,还有___。
0
有理数还有其他的分类方法吗?
讲授新课
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数按符号(正、负)分类如下:
注意: ①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数。
讲授新课
典例精析
【例2】下列说法中错误的是( )
A.正有理数、零、负有理数统称为有理数
B.正数与零统称为非负数
C.非正数都比零小 D.正整数和正分数组成正有理数
【详解】正有理数、零、负有理数统称为有理数,
选项A不符合题意;
正数与零统称为非负数,选项B不符合题意;
非正数都小于或等于0,选项C符合题意;
正整数和正分数组成正有理数,选项D不符合题意.
故选C.
讲授新课
练一练
1.给出下列各数:4.443,0,3.1159,-1000,,其中分数的个数是m,非正数的个数是n,则m+n= .
【详解】解:∵4.443,3.1159, ,是分数,
∴m=3,
∵0,-1000,是非正数,
∴n=3,
∴m+n=3+3=6.
故答案为:6.
讲授新课
2.把下列各数填在相应的表示集合的大括号里:4,0.5,,10%,-5,-3.14,0,,+2022,
(1)正整数集合{ };
(2)分数集合{ };
(3)负分数集合{ };
(4)整数集合{ }.
【详解】(1)解:正整数集合为:4,+2022;
(2)解:分数集合为:0.5,,10%,-3.14,;
(3)解:负分数集合为:,-3.14;
(4)解:整数集合为:4,-5,0,+2022
讲授新课
知识点三 带“非”字的有理数
非负数是 ,
非正数是 ,
非负整数是 ,
非正整数是 .
零和正数
零和正整数
零和负数
零和负整数
1、零是______________________________;
2、零不是_____________________________;
正数, 不是负数, 也不是分数
自然数, 是整数, 是有理数
讲授新课
典例精析
【例3】在-15,,-0.23,0,7.6,2,,314%.这八个有理数中非负数有( )
A.4个 B.5个 C.6个 D.7个
【详解】解:在-15, ,-0.23,0,7.6,2, ,3.14%这八个数中,
非负数为,0,7.6,2,314%,有5个.
故选:B.
讲授新课
练一练
1.有理数2,+7.5,-0.03,-0.4,0,,10中,非负整数有 个.
【详解】解:有理数2,+7.5,-0.03,-0.4,0, ,10中,非负整数有2,0,10共3个,
故答案为:3.
当堂检测
1.下列各数中,是正分数的是( )
A. B.0 C.3 D.2.5
【详解】A、是负分数,此选项不符合题意,排除;
B、0既不是正数,也不是负数,此选项不符合题意,排除;
C、3是整数,此选项不符合题意,排除;
D、2.5是正分数,此选项符合题意;
故选:D.
当堂检测
2.在一组数-2,0.4,0,π,,,3.5151151115···(相邻的两个5之间依次多一个1)中,有理数的个数是( )
A.3 B.4 C.5 D.6
【详解】解:在实数-2,0.4,0,π, , ,3.5151151115···(相邻的两个5之间依次多一个1)中,有理数有-2,0.4,0,,,共5个.
故选:C.
当堂检测
3.下列说法①正整数和负整数统称整数②零既不是正数,也不是非负数③有理数除整数外,其余全是分数④正分数和负分数统称为分数.其中正确的有( )
A.0个 B.1个 C.2个 D.3
【详解】正整数、负整数和0统称整数,故①错误;
零是非负数,故②错误;
有理数除整数外,其余全是分数,故③正确;
正分数和负分数统称为分数,故④正确;
故选:C.
当堂检测
4.大于-4且小于3.2的所有整数的和等于 .
【详解】解:由题意得:大于-4而小于3.2的整数有:-3,-2,-1,0,1,2,3,
∴(-3)+(-2)+(-1)+0+1+2+3=0,
故答案为:0.
当堂检测
5.有理数-1.7,-17,0,,-1,,-0.001,2003中,负分数有 个.
【详解】解:负分数有:-1.7,,,-0.001,共4个,
故答案为:4.
当堂检测
6.在,,0,-1,0.4,π,2,-3,-6这些数中,有理数有m个,自然数有n个,分数有k个,则m-n-k的值为 .
【详解】∵ , ,0,-1,0.4,π,2,-3,-6,
∴有理数有m=8个,自然数有n=2个,分数有k=3个,
∴m-n-k=8-2-3=3,
故答案为:3.
当堂检测
7.把下列各数填入相应集合的括号内.
+6.5,,0.5,0,-3.2,13,-9,,-1,-3.6,
(1)正分数集合:{____________…};
(2)整数集合:{____________…};
(3)非负数集合:{____________…).
【详解】(1)解:根据正分数的定义,正分数有:+6.5,0.5,,
故答案为:+6.5,0.5, ;
(2)解:根据整数的定义,整数有:0,13,-9,-1,
故答案为:0,13,-9,-1;
(3)解:根据非负数的定义,非负数有:+6.5,0.5,0,13,,,
故答案为:+6.5,0.5,0,13, , .
当堂检测
8.“不是正数的数一定是负数,不是负教的数一定是正数”的说法对吗?为什么?
【详解】不对.因为0既不是正数也不是负数.
当堂检测
9.把下列各数按要求分类:5.2,0,,,+(-4),,-(-3),0.2555···,-0.030030003···.
(1)写出所有的分数;
(2)写出所有的非负整数;
(3)写出所有的有理数.
【详解】(1)分数集合:{5.2,,,0.2555……}.
(2)非负整数集合:{0,-(-3)}.
(3)有理数集合:{ 5.2,0,,+(-4),,-(-3),0.2555……}.
课堂小结
1.整数和分数统称为有理数;(目前我们学过的数中,只有π不是有理数)
2.有理数的分类
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
3.注意0的特殊性,在分类时千万不要遗漏0.
谢 谢~
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
