3.3勾股定理的应用举例 同步练习(含答案)鲁教版(五四制)初中数学七年级上册
文档属性
| 名称 | 3.3勾股定理的应用举例 同步练习(含答案)鲁教版(五四制)初中数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 378.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览



文档简介
3.3勾股定理的应用举例同步练习-鲁教版(五四制)初中数学七年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
2.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长的直吸管露在罐外部分的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. B. C. D.
3.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
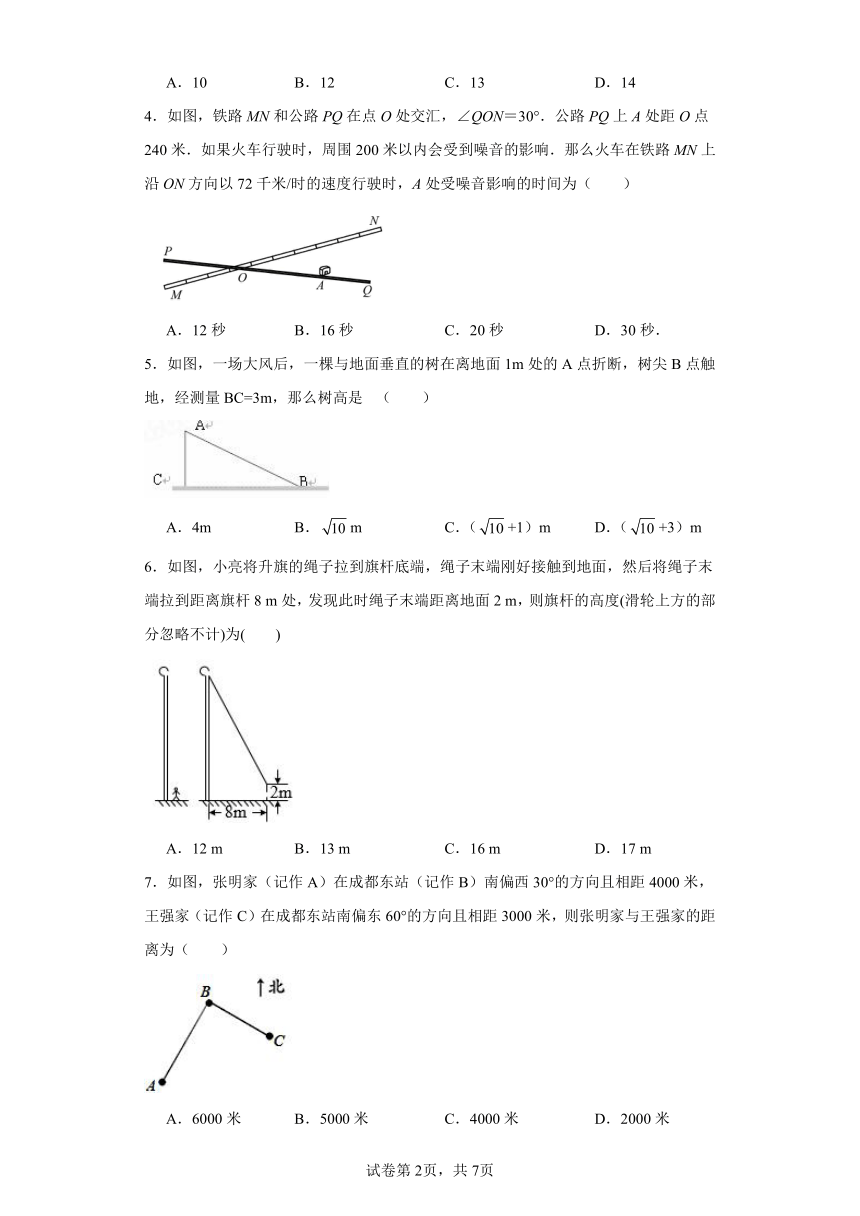
4.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
A.12秒 B.16秒 C.20秒 D.30秒.
5.如图,一场大风后,一棵与地面垂直的树在离地面1m处的A点折断,树尖B点触地,经测量BC=3m,那么树高是 ( )
A.4m B.m C.(+1)m D.(+3)m
6.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m C.16 m D.17 m
7.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
A.6000米 B.5000米 C.4000米 D.2000米
8.已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )
A.海里 B.海里 C.16海里 D.24海里
9.(数学文化)我国古代著作《九章算术》中有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何.”其大意为:有一水池一丈见方,池中间生有一颗类似芦苇的植物,露出水面一尺,若把它引向岸边,正好与岸边平齐(如图),问水有多深,该植物有多长?其中一丈为十尺,设水深为尺,则可列方程为( )
A. B.
C. D.
10.一根竹子高一丈,折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度是多少?(这是我国古代《九章算术》中的“折竹抵地问题.其中的丈、尺是长度单位,一丈=10尺)设折断处离地面的高度为x尺,则可列方程为( )
A.x2+62=(10﹣x)2 B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2 D.x2﹣6=(10﹣x)2
二、填空题
11.如图,是台阶的示意图,已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于 .
12.一种圆柱形口杯(厚度忽略不计),测得内部底面半径为,高为.吸管如图放进杯里,杯口外面露出部分长为,则吸管的长度为 .
13.有一棵9米高的大树,如果大树距离地面4米处这段(没有断开),则小孩至少离开大树 米之处才是安全的.
14.如图,客船以24海里/时的速度从港口向东北方向航行,货船以18海里/时的速度同时从港口向东南方向航行,则1小时后两船相距 海里.
15.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处离远处竹子的距离为3尺,则原处还有竹子 尺.(请直接写出答案,注:1丈=10尺.)
16.如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为 cm.
17.如图,把直角三角形纸片折叠,使点C落在C′处,折痕为AD,得到∠CDC′=60°.若∠ABC=90°,AB=1,AC=,则CD= .
18.如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程为 .
19.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为 m.
20.如图,一根树在离地面3米处断裂,树的顶部落在离底部4米处.树折断之前有 米.
三、解答题
21.如图,一架云梯AB长25m,斜靠在一面墙上,梯子靠墙的一端A距地面24m.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
22.如图,一架长的梯子斜靠在一竖直的墙上,这时为,如果梯子的顶端尚墙下滑,那么梯子底端向外移了多少米?(注意:)
23."引葭赴岸“是《九章算木》中的一道题:”今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸芥.伺水深,葭氏各几何 "题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'.向芦苇长多少 (画出几何图形并解答)
24.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
25.由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB = 1米,BC = 5米,两棵树的株距(两棵树的水平距离)为3米,在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.C
4.B
5.C
6.D
7.B
8.B
9.D
10.A
11.195cm/195厘米
12.17
13.3
14.30
15.
16.
17.
18.
19.
20.8
21.(1)7米;(2)8m
22.梯子底端向外移了
23.13尺
24.旗杆的高度为12米.
25.蚂蚁沿着A-B-D路线走最近.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
2.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长的直吸管露在罐外部分的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. B. C. D.
3.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
4.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
A.12秒 B.16秒 C.20秒 D.30秒.
5.如图,一场大风后,一棵与地面垂直的树在离地面1m处的A点折断,树尖B点触地,经测量BC=3m,那么树高是 ( )
A.4m B.m C.(+1)m D.(+3)m
6.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m C.16 m D.17 m
7.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
A.6000米 B.5000米 C.4000米 D.2000米
8.已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )
A.海里 B.海里 C.16海里 D.24海里
9.(数学文化)我国古代著作《九章算术》中有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何.”其大意为:有一水池一丈见方,池中间生有一颗类似芦苇的植物,露出水面一尺,若把它引向岸边,正好与岸边平齐(如图),问水有多深,该植物有多长?其中一丈为十尺,设水深为尺,则可列方程为( )
A. B.
C. D.
10.一根竹子高一丈,折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度是多少?(这是我国古代《九章算术》中的“折竹抵地问题.其中的丈、尺是长度单位,一丈=10尺)设折断处离地面的高度为x尺,则可列方程为( )
A.x2+62=(10﹣x)2 B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2 D.x2﹣6=(10﹣x)2
二、填空题
11.如图,是台阶的示意图,已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于 .
12.一种圆柱形口杯(厚度忽略不计),测得内部底面半径为,高为.吸管如图放进杯里,杯口外面露出部分长为,则吸管的长度为 .
13.有一棵9米高的大树,如果大树距离地面4米处这段(没有断开),则小孩至少离开大树 米之处才是安全的.
14.如图,客船以24海里/时的速度从港口向东北方向航行,货船以18海里/时的速度同时从港口向东南方向航行,则1小时后两船相距 海里.
15.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处离远处竹子的距离为3尺,则原处还有竹子 尺.(请直接写出答案,注:1丈=10尺.)
16.如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为 cm.
17.如图,把直角三角形纸片折叠,使点C落在C′处,折痕为AD,得到∠CDC′=60°.若∠ABC=90°,AB=1,AC=,则CD= .
18.如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程为 .
19.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为 m.
20.如图,一根树在离地面3米处断裂,树的顶部落在离底部4米处.树折断之前有 米.
三、解答题
21.如图,一架云梯AB长25m,斜靠在一面墙上,梯子靠墙的一端A距地面24m.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
22.如图,一架长的梯子斜靠在一竖直的墙上,这时为,如果梯子的顶端尚墙下滑,那么梯子底端向外移了多少米?(注意:)
23."引葭赴岸“是《九章算木》中的一道题:”今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸芥.伺水深,葭氏各几何 "题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'.向芦苇长多少 (画出几何图形并解答)
24.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
25.由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图所示,其树恰好落在另一棵树乙的根部C处,已知AB = 1米,BC = 5米,两棵树的株距(两棵树的水平距离)为3米,在点A有一只蚂蚁想尽快爬到位于B、C两点之间的D处,且CD=0.1米,问它怎样走最近?为什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.C
4.B
5.C
6.D
7.B
8.B
9.D
10.A
11.195cm/195厘米
12.17
13.3
14.30
15.
16.
17.
18.
19.
20.8
21.(1)7米;(2)8m
22.梯子底端向外移了
23.13尺
24.旗杆的高度为12米.
25.蚂蚁沿着A-B-D路线走最近.
答案第1页,共2页
答案第1页,共2页
