6.3一次函数的图像 同步练习(含答案)鲁教版(五四制)初中数学七年级上册
文档属性
| 名称 | 6.3一次函数的图像 同步练习(含答案)鲁教版(五四制)初中数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 240.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览

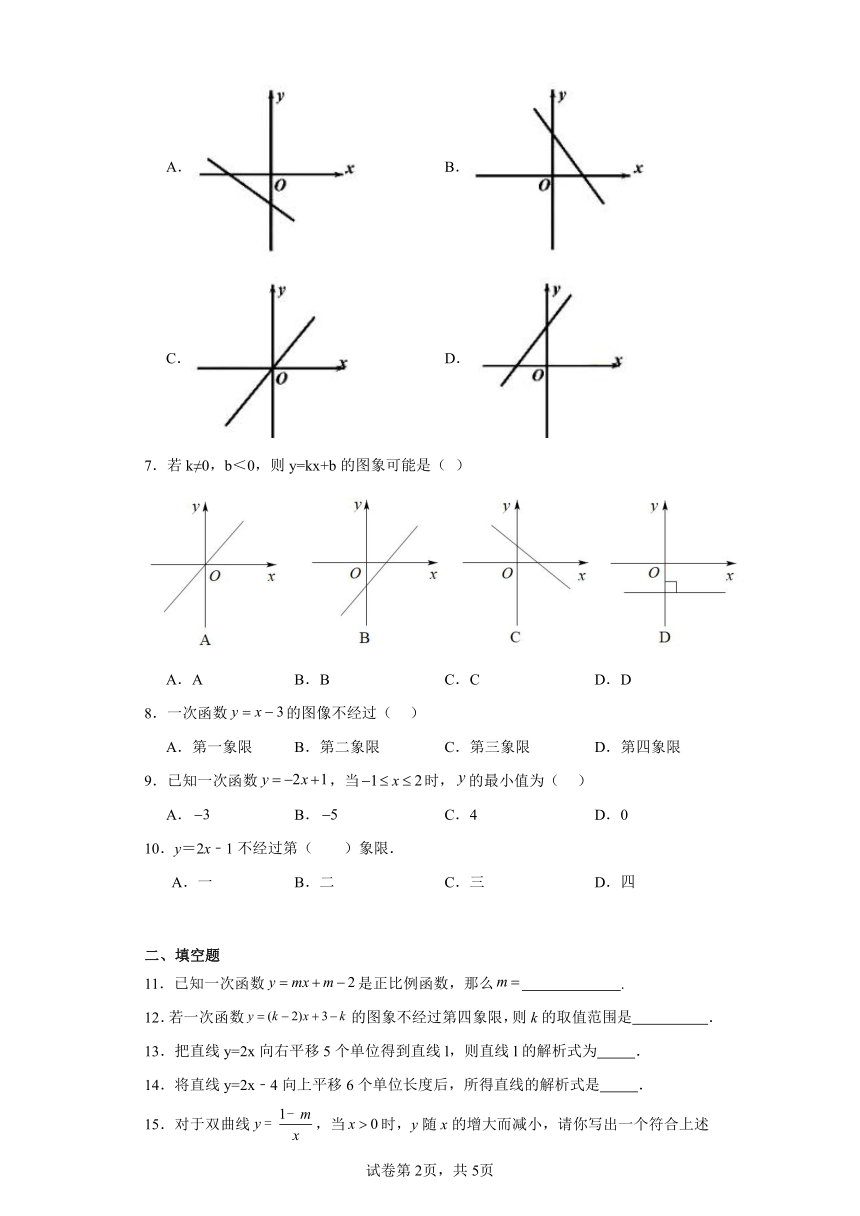


文档简介
6.3一次函数的图像同步练习-鲁教版(五四制)初中数学七年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,是一次函数的图象上的两点,则与的大小关系是
A. B. C. D.以上都不对
2.已知一次函数,要使函数值随自变量增大而增大,则的取值范围是( )
A. B. C. D.
3.以下四种情境分别描述了两个变量之间的关系:甲:东乐投篮时,投出去的篮球的高度与时间的关系;乙:乐乐去文具店购买签字笔,支付费用与购买签字笔支数的关系;丙:一长方形水池里还有一部分水,再打开水管匀速往里注水,注水时间和水池中水面的高度之间的关系;丁:乐乐去奶奶家吃饭,饭后,按原速度原路返回,乐乐离家的距离与时间的关系.用下面的图象刻画上述情境,排序正确的是( )
A.①②③④ B.①③④② C.①④②③ D.①③②④
4.已知函数y=(m﹣3)x﹣(m是常数),当m取何值时,y随x的增大而减小( )
A.m=3 B.m>3 C.m<3 D.m≤3
5.在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是( )
A.第一象限 B.第二象限 C.第四象限 D.不能确定
6.已知一次函数,随着的增大而减小,且,则它的大致图象是( )
A. B.
C. D.
7.若k≠0,b<0,则y=kx+b的图象可能是( )
A.A B.B C.C D.D
8.一次函数的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知一次函数,当时,的最小值为( )
A. B. C.4 D.0
10.y=2x﹣1不经过第( )象限.
A.一 B.二 C.三 D.四
二、填空题
11.已知一次函数是正比例函数,那么 .
12.若一次函数的图象不经过第四象限,则k的取值范围是 .
13.把直线y=2x向右平移5个单位得到直线l,则直线l的解析式为 .
14.将直线y=2x﹣4向上平移6个单位长度后,所得直线的解析式是 .
15.对于双曲线,当时,y随x的增大而减小,请你写出一个符合上述要求的m的值 .
16.将一次函数y=x+3的图象沿着y轴向下平移5个单位,那么平移后所得图象的函数解析式为 .
17.如图,直线AB与x轴、y轴分别交于点A和点B,且,点B的坐标为,过点A的直线与y轴交于点,将直线AC向上平移2个单位长度后得到直线,则的值为 .
18.如图,在平面直角坐标系中,直线:与轴交于点,如图所示依次作正方形、正方形、…、正方形,使得点、、、…在直线上,点、、、…在轴正半轴上,则点的坐标是 .
19.在一次函数,y随x的增大而增大,则m的取值范围是 .
20.一次函数与正比例函数的图象平行且经过点(1,﹣1),则的值为 .
三、解答题
21.已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
22.八年级(1)班张山同学利用所学函数知识,对函数进行了如下研究:
列表如下:
x … 0 1 2 3 …
y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:________,________;
(3)在给出的坐标系中画出函数的图象;
(4)一次函数的图象与函数的图象交点的坐标为_______.
23.如图,在平面直角坐标系中,直线AB:与轴交于点C,且点,.
(1)点C的坐标为
(2)求原点O到直线的距离;
(3)在x轴上是否存在一点P,使得是直角三角形 若存在,求出点P的坐标.
24.已知函数y=(2m+1)x+m﹣3;
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴的截距为﹣2,求m的值;
(3)若函数的图象平行直线y=3x﹣3,求m的值;
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
25.作出函数y=2x-4的图象,并根据图象回答下列问题:
(1)当-2≤x≤4时,求函数y的取值范围;
(2)当x取什么值时,y<0,y=0,y>0
(3)当x取何值时,-4试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.C
4.C
5.A
6.B
7.B
8.B
9.A
10.B
11.2
12.<
13.
14.y=2x+2
15.0(答案不唯一)
16.y=
17.1
18.(22020,22021-1)
19./
20.-4
21.±4
22.(1)全体实数;(2)1,1;(3)略;(4)和.
23.(1);
(2);
(3)存在,点的坐标为或
24.(1)m=3;(2)m=1;(3)m=1;(4)m<﹣.
25.(1) 8≤y≤4;(2)当x=2时,y=0;当x>2时,y>0;当x<2时,y<0;(3):0答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,是一次函数的图象上的两点,则与的大小关系是
A. B. C. D.以上都不对
2.已知一次函数,要使函数值随自变量增大而增大,则的取值范围是( )
A. B. C. D.
3.以下四种情境分别描述了两个变量之间的关系:甲:东乐投篮时,投出去的篮球的高度与时间的关系;乙:乐乐去文具店购买签字笔,支付费用与购买签字笔支数的关系;丙:一长方形水池里还有一部分水,再打开水管匀速往里注水,注水时间和水池中水面的高度之间的关系;丁:乐乐去奶奶家吃饭,饭后,按原速度原路返回,乐乐离家的距离与时间的关系.用下面的图象刻画上述情境,排序正确的是( )
A.①②③④ B.①③④② C.①④②③ D.①③②④
4.已知函数y=(m﹣3)x﹣(m是常数),当m取何值时,y随x的增大而减小( )
A.m=3 B.m>3 C.m<3 D.m≤3
5.在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是( )
A.第一象限 B.第二象限 C.第四象限 D.不能确定
6.已知一次函数,随着的增大而减小,且,则它的大致图象是( )
A. B.
C. D.
7.若k≠0,b<0,则y=kx+b的图象可能是( )
A.A B.B C.C D.D
8.一次函数的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知一次函数,当时,的最小值为( )
A. B. C.4 D.0
10.y=2x﹣1不经过第( )象限.
A.一 B.二 C.三 D.四
二、填空题
11.已知一次函数是正比例函数,那么 .
12.若一次函数的图象不经过第四象限,则k的取值范围是 .
13.把直线y=2x向右平移5个单位得到直线l,则直线l的解析式为 .
14.将直线y=2x﹣4向上平移6个单位长度后,所得直线的解析式是 .
15.对于双曲线,当时,y随x的增大而减小,请你写出一个符合上述要求的m的值 .
16.将一次函数y=x+3的图象沿着y轴向下平移5个单位,那么平移后所得图象的函数解析式为 .
17.如图,直线AB与x轴、y轴分别交于点A和点B,且,点B的坐标为,过点A的直线与y轴交于点,将直线AC向上平移2个单位长度后得到直线,则的值为 .
18.如图,在平面直角坐标系中,直线:与轴交于点,如图所示依次作正方形、正方形、…、正方形,使得点、、、…在直线上,点、、、…在轴正半轴上,则点的坐标是 .
19.在一次函数,y随x的增大而增大,则m的取值范围是 .
20.一次函数与正比例函数的图象平行且经过点(1,﹣1),则的值为 .
三、解答题
21.已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
22.八年级(1)班张山同学利用所学函数知识,对函数进行了如下研究:
列表如下:
x … 0 1 2 3 …
y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:________,________;
(3)在给出的坐标系中画出函数的图象;
(4)一次函数的图象与函数的图象交点的坐标为_______.
23.如图,在平面直角坐标系中,直线AB:与轴交于点C,且点,.
(1)点C的坐标为
(2)求原点O到直线的距离;
(3)在x轴上是否存在一点P,使得是直角三角形 若存在,求出点P的坐标.
24.已知函数y=(2m+1)x+m﹣3;
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴的截距为﹣2,求m的值;
(3)若函数的图象平行直线y=3x﹣3,求m的值;
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
25.作出函数y=2x-4的图象,并根据图象回答下列问题:
(1)当-2≤x≤4时,求函数y的取值范围;
(2)当x取什么值时,y<0,y=0,y>0
(3)当x取何值时,-4
试卷第1页,共3页
参考答案:
1.A
2.B
3.C
4.C
5.A
6.B
7.B
8.B
9.A
10.B
11.2
12.<
13.
14.y=2x+2
15.0(答案不唯一)
16.y=
17.1
18.(22020,22021-1)
19./
20.-4
21.±4
22.(1)全体实数;(2)1,1;(3)略;(4)和.
23.(1);
(2);
(3)存在,点的坐标为或
24.(1)m=3;(2)m=1;(3)m=1;(4)m<﹣.
25.(1) 8≤y≤4;(2)当x=2时,y=0;当x>2时,y>0;当x<2时,y<0;(3):0
答案第1页,共2页
