广东省各地区近两年小升初真题题型汇编专项训练 题型四解答题57题(二)(人教版)(含解析)
文档属性
| 名称 | 广东省各地区近两年小升初真题题型汇编专项训练 题型四解答题57题(二)(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 05:12:09 | ||
图片预览




文档简介
题型四 解答题57题(二)(人教版)
广东省各地区近两年小升初真题题型汇编专项训练
一、解答题。
(2022·广东梅州·统考小升初真题)
1.全班46人去客天下游览。门口的购票须知上写着:门票每人85元50人开始可以享受八折优惠。你认为怎样购票花钱最少,最少要用多少钱?
(2022·广东汕头·统考小升初真题)
2.“五一”商场举行促销活动,一款双开门冰箱原标价6000元,现价九折出售,便宜了多少元?
(2021·广东广州·统考小升初真题)
3.接种新冠肺炎疫苗是“外防输入,内防反弹”的必要举措。某社区卫生服务中心某天上午为人民群众免费接种新冠肺炎疫苗600支,比下午多接种20%。下午为人民群众接种新冠肺炎疫苗多少支?
(2021·广东汕尾·统考小升初真题)
4.水是由氢和氧按1∶8的质量比化合而成的。6.3的水含氢和氧各多少?
(2022·广东韶关·统考小升初真题)
5.在比例尺1∶50000000的地图上,量得广州到北京的距离是4.4厘米,一架飞机从广州飞往北京,4小时到达。这架飞机平均每小时飞行多少千米?
(2022·广东江门·统考小升初真题)
6.学校合唱队共有45位同学,其中男生的人数是女生的,合唱队里男生和女生各有多少人?(列方程解答)
(2022·广东广州·统考小升初真题)
7.学校举行六年级美术作品征集比赛。六(1)班提交了48件作品,六(2)班提交的作品比六(1)班多,六(3)班和六(2)班提交的作品件数比是5∶6。
(1)六(2)班提交了多少件作品?
(2)六(3)班提交了多少件作品?
(2022·广东广州·统考小升初真题)
8.一列高铁从杭州开往上海,已经行了全程的,恰好距离中点16.8千米处。杭州到上海高铁路线全程多少千米?先把线段图补充完整(请在线段图中标出“16.8千米”和要求的问题。)并解答。
(2022·广东广州·统考小升初真题)
9.一个圆柱形橡皮泥,底面半径是2厘米,高是5厘米。
(1)这个橡皮泥的表面积是多少平方厘米?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
(2022·广东梅州·统考小升初真题)
10.现有空的长方体容器A和水深24厘米的长方体容器B(如图),要将容器B的水倒一部分给A,使两容器水的高度相同,这时水深是几厘米?
(2022·广东阳江·统考小升初真题)
11.王大妈把6000元存入银行,定期5年,准备到期后把利息捐赠给福利院。如果年利率按4.22%计算,到期后她可以捐出多少元?
(2022·广东阳江·统考小升初真题)
12.有一个底面直径10米,高1.8米圆柱形水池,如果在水池内壁和底面都要贴上瓷砖,这个水池贴瓷砖的面积是多少平方米?
(2022·广东珠海·统考小升初真题)
13.芳芳用卡纸制作了一个底面直径是10厘米,高12厘米的笔筒,至少需要多少平方厘米的卡纸?
(2022·广东珠海·统考小升初真题)
14.在一幅比例尺是1∶30000000的地图上,量得两城市之间的距离是2.7厘米,一列货车和一列客车分别从两地同时相对开出,5小时后相遇。货车的速度是72千米/时,客车的速度是多少?
(2022·广东珠海·统考小升初真题)
15.一个圆锥形沙堆,底面积是31.4平方米,高是2.4米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
(2022·广东汕头·统考小升初真题)
16.一套运动服的价格是144元,裤子和上衣价格的比是7∶9,裤子的价格是多少元?
(2022·广东汕头·统考小升初真题)
17.一个圆柱形粮囤,从里面量得底面半径是1.5米,高2米。如果每立方米玉米约重750千克,这个粮囤能装多少千克玉米?
(2021·广东广州·统考小升初真题)
18.为了学生的卫生安全,学校给每个学生配一个水杯,每只水杯4元,美好家园打九折,汇集超市“买七送一”。学校想买160只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
(2021·广东广州·统考小升初真题)
19.一辆汽车从甲城开往乙城6小时到达,返回时减慢了速度,每小时比原来少行5千米,结果用了8小时就回到了甲城,求甲城到乙城的路程有多少千米?
(2021·广东深圳·统考小升初真题)
20.建于明永乐十八年(1420)的北京天坛祈年殿已有600年历史。祈年殿为砖木结构,殿高约38米,底层直径约32米,三层重檐向上逐层收缩作伞状。殿内有28根金丝楠木大柱,内围的4根“龙井柱”象征春、夏、秋、冬四季,每根高约19米,直径1.2米。如果要给这4根“龙井柱”刷上油漆,则刷漆面积共是多少平方米?(本题π值取3)
(2021·广东深圳·统考小升初真题)
21.在比例尺是1∶4000000的交通地图上,量得深圳福田站到北京西站的长度约60厘米。从福田站开往北京西站的G72动车每小时约行225千米,G72动车从福田站运行到北京西站大约需要多少时间?(不考虑列车途中靠站停留等因素)
(2021·广东深圳·统考小升初真题)
22.我国首次火星探测即实现着陆(2021年5月15日)的“祝融号”火星车高度是苏联的火星探测器“火星1号”(未着陆成功)的多1厘米,“火星1号”高230厘米。“祝融号”高多少厘米?
(2021·广东深圳·统考小升初真题)
23.联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,环保小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将结果分析整理制作成了下面两个统计图。其中:
A是能将垃圾放在规定的地方,而且还会考虑垃圾的分类
B是能将垃圾放在规定的地方,但不会考虑垃圾的分类。
C是偶尔会将垃圾放在规定的地方。
D是随手乱扔垃圾。
根据以上信息回答问题。
(1)该校环保小组共调查了( )人。
(2)请补全条形统计图。
(2021·广东阳江·统考小升初真题)
24.建筑工人使用一个圆锥形的铅锤来判断建筑物是否垂直,这个铅锤底面半径2cm,高6cm,每立方厘米铅锤约重7.8g,这个铅锤重多少g?
(2021·广东阳江·统考小升初真题)
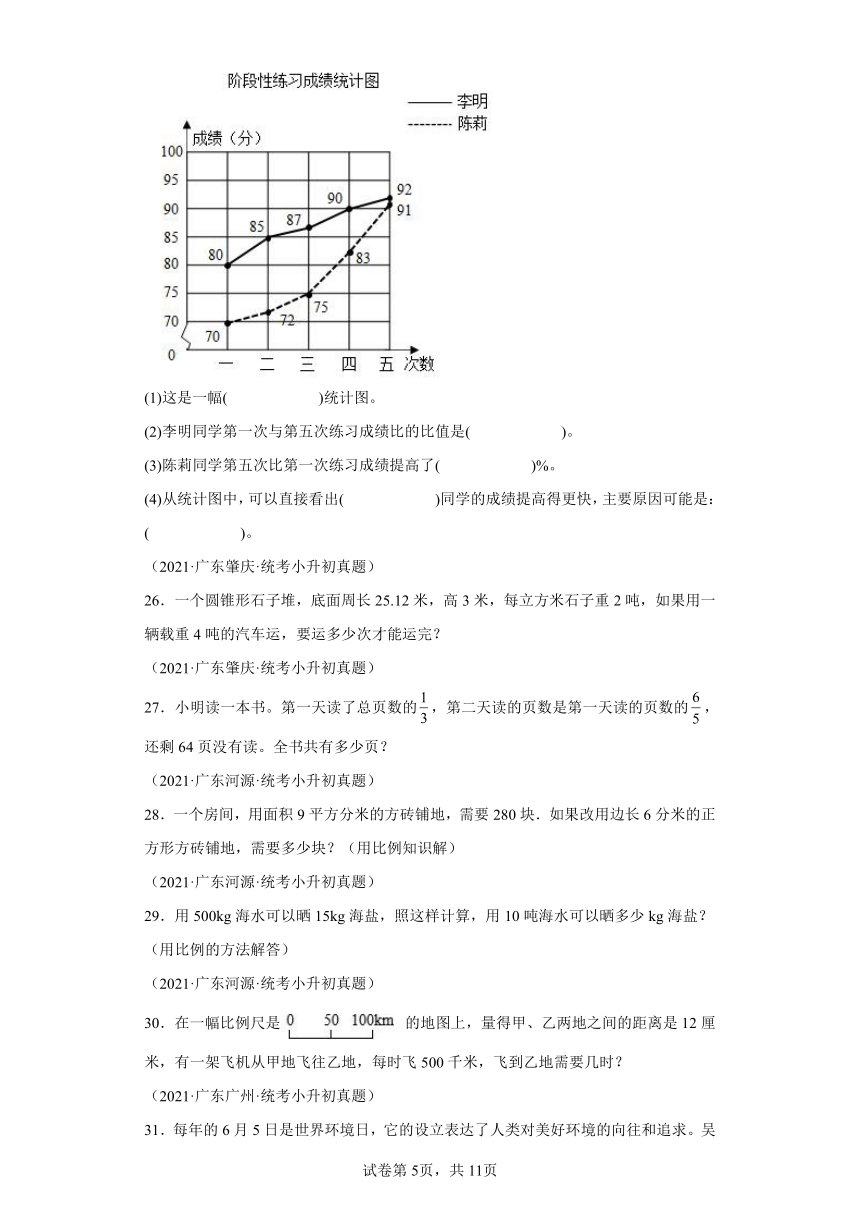
25.在抗击新冠肺炎期间,甲和乙两位同学按照“停课不停学”要求,合理安排时间并进行阶段练习。(如图)
(1)这是一幅( )统计图。
(2)李明同学第一次与第五次练习成绩比的比值是( )。
(3)陈莉同学第五次比第一次练习成绩提高了( )%。
(4)从统计图中,可以直接看出( )同学的成绩提高得更快,主要原因可能是:( )。
(2021·广东肇庆·统考小升初真题)
26.一个圆锥形石子堆,底面周长25.12米,高3米,每立方米石子重2吨,如果用一辆载重4吨的汽车运,要运多少次才能运完?
(2021·广东肇庆·统考小升初真题)
27.小明读一本书。第一天读了总页数的,第二天读的页数是第一天读的页数的,还剩64页没有读。全书共有多少页?
(2021·广东河源·统考小升初真题)
28.一个房间,用面积9平方分米的方砖铺地,需要280块.如果改用边长6分米的正方形方砖铺地,需要多少块?(用比例知识解)
(2021·广东河源·统考小升初真题)
29.用500kg海水可以晒15kg海盐,照这样计算,用10吨海水可以晒多少kg海盐?(用比例的方法解答)
(2021·广东河源·统考小升初真题)
30.在一幅比例尺是的地图上,量得甲、乙两地之间的距离是12厘米,有一架飞机从甲地飞往乙地,每时飞500千米,飞到乙地需要几时?
(2021·广东广州·统考小升初真题)
31.每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。吴芳家为了节约用水,订做了一个圆柱形铁皮水桶(无盖)蓄水,高8dm,底面直径是高的。做这个水桶至少要用多少铁皮?
(2021·广东广州·统考小升初真题)
32.“六一”儿童节前夕,某品牌的玩具搞促销活动。在A商场打六折出售,在B商场按“每满100元减40元”的方式销售。妈妈要买一个标价240元的这种品牌的玩具。
(1)在A、B两个商场买各应付多少钱?
(2)选择哪个商场更省钱?
(2021·广东广州·统考小升初真题)
33.工地上有一个圆锥形的沙堆,高是1.8米,底面半径是5米,每立方米的沙约重1.7吨。这堆沙约重多少吨?(得数保留整吨)
(2021·广东广州·统考小升初真题)
34.小军在校篮球比赛中,2分球和3分球一共进了8个,共获得18分,小军的2分球和3分球各投进多少个?
(2021·广东广州·统考小升初真题)
35.食堂有一些大米,第一周吃掉了总数的35%,第二周吃掉了180千克,这时剩下的大米与吃掉了的大米一样多.食堂原来有大米多少千克?
(2021·广东广州·统考小升初真题)
36.一本故事书共120页,红红第一天看了,第二天看了余下的,两天一共看了多少页?
(2021·广东汕尾·统考小升初真题)
37.某家电销售第一季度的营业额为15万元,第二季度的营业额为16.5万元。第二季度的营业额比第一季度增长了百分之多少?
(2021·广东汕尾·统考小升初真题)
38.下图中的每小格表示边长1厘米的正方形。
(1)按2∶1的比画出三角形放大后的图形。
(2)放大后三角形的面积是( )平方厘米。
(2021·广东深圳·统考小升初真题)
39.校园内有棵老树长得很高,淘气量出这棵老树的影子长为8.7米,同时在老树的附近竖立一根米尺(长度为1米),量得米尺的影子长为0.6米。这棵老树的高度是多少米?(用比例解答)
(2021·广东深圳·统考小升初真题)
40.笑笑家最近购买了一台电热水器(外壳和内胆均为近似的圆柱体),外壳长为6分米,底面直径为4分米,内胆从里边量长为5分米,底面直径为3分米。
(1)外壳的表面积是多少平方分米?
(2)内胆的容积约是多少升?(结果取整数)
(2021·广东深圳·统考小升初真题)
41.下面是某小学学生参加“430校内课后服务”项目的抽样调查统计图,根据信息完成下面各题。
(1)抽样调查总人数有多少人?
(2)把条形统计图补充完整。
(3)“足球”的人数比“演讲”的人数少百分之几?
(2021·广东深圳·统考小升初真题)
42.在比例尺是1∶5000000的地图上,量得甲地到乙地的图上距离是9厘米。李老师一家上午8:00驾车从甲地前往乙地小车平均每小时行驶100千米。
(1)上午11:00时小车行驶至哪里?请在图中用“”标出,并简要说明理由。
(2)小车每行驶100千米消耗汽油8升,出发时油箱里有40升汽油,中途还需要再加油吗?(写出计算过程)
(3)上午11:00后,由于路上车流量增加,小车的平均速度下降了10%,那么李老师到达乙地的最早时间是几点几分?
(2021·广东东莞·统考小升初真题)
43.一个圆锥形零件,从上面看到的图形如图1,从前面看到的图形如图2(图中每个小正方形的边长表示1cm),这个零件的体积是多少立方厘米?
(2021·广东东莞·统考小升初真题)
44.一个正方体玻璃容器(无盖)的棱长是2分米。
(1)做这个玻璃容器至少需要多少平方分米的玻璃?
(2)向容器中倒入5升水,再把一个土豆没入水中。这时量得容器内水深14厘米。土豆的体积是多少?(玻璃的厚度忽略不计)
(2021·广东东莞·统考小升初真题)
45.2020年新冠肺炎爆发,疫情的蔓延牵动着每个人的心。图1呈现了某地连续7天新增新冠肺炎确诊病例的统计结果,图2是对这些病人发病原因的进一步调查。
(1)请将图2补充完整。
(2)请根据图1提一个需要用除法和加法解决的问题。(提出问题并列出算式,不用计算)
问题:__________________________________________________________________________
列式:__________________________________________________________________________
(3)根据图2,给该地区市民提一条防疫建议,并说明理由。
_________________________________________________________________________________
_________________________________________________________________________________
(2022·广东江门·统考小升初真题)
46.下图是2021年2月四家快递公司业务量。
(1)2021年2月,申通快递的业务量是韵达快递业务量的百分之几?(百分号前保留整数)
(2)顺丰快递2021年2月的业务量比2020年2月增长了40%,顺丰快递2020年2月的快递业务量约是多少百万件?(得数保留整数)
(2022·广东潮州·统考小升初真题)
47.夏令营组织学生行军训练。去时每小时行3.6千米,2小时到达目的地。返程速度减慢一些,每小时行3.2千米,几小时可回到出发地?(用比例知识解答)
(2022·广东潮州·统考小升初真题)
48.一对无盖的圆柱形铁皮水桶,底面直径20厘米,高30厘米。
(1)做这样一对水桶大约需要多少平方分米铁皮?(得数保留整数)
(2)这对水桶可以装水多少升?(铁皮厚度忽略不计)
(2022·广东潮州·统考小升初真题)
49.一个果园,种桃树的面积占果园总面积的,种李子树的面积是2.5公顷,余下的地种樱桃树。已知种桃树和李子树的总面积与种樱桃树的面积的比是7︰5,种樱桃树的面积是多少公顷?
(2022·广东韶关·统考小升初真题)
50.淘气妈妈计划购买一双价值400元的皮鞋,甲乙两个商场优惠活动如下:甲商场凡消费满300元返现金40元;乙商场商品一律打八五折。淘气妈妈到哪个商场购买更优惠?
(2022·广东韶关·统考小升初真题)
51.一个圆锥形稻谷堆,高18分米,占地面积10平方米,把这堆稻谷全部装入一个圆柱形粮仓,正好占整个粮仓的20%,求这个粮仓的容积。
(2022·广东阳江·统考小升初真题)
52.有甲、乙两袋大米,甲袋有60千克,从甲袋取出,从乙袋取出25%后,甲、乙两袋剩余大米的质量比是8∶3。乙袋中原来有多少千克大米?
(2022·广东珠海·统考小升初真题)
53.为鼓励居民节约用水,珠海市规定每户每月用水按阶梯收费,如图:
等级 用水量(立方米) 收费标准(元/立方米)
第一级 20或20以下 1.74
第二级 20以上且a或a以下 2.61
第三级 a以上 3.84
下面是乐乐家近三个月月末的水表读数及交费情况:
月份 四月 五月 六月
月末水表读数(立方米) 86 111 143
本月交水费(元) 31.32 47.85 68.58
(1)乐乐家六月份用水多少立方米?
(2)当用水多少立方米以上时收费标准是3.84元/立方米?
(2021·广东广州·统考小升初真题)
54.客车和货车分别从甲乙两站同时相向开出,5小时后相遇,相遇后两车仍按原速度前进,当他们相距196千米时,客车行了全程的,货车行了全程的80%。
(1)全程是多少千米?
(2)货车行完全程需要多少个小时?
(2021·广东肇庆·统考小升初真题)
55.两年前,小芳将500元压岁钱存入银行,年利率4.50%。今年到期时,小芳准备用实得利息购买下面的书包,钱够不够?(银行利息税5%)
(2021·广东广州·统考小升初真题)
56.王大伯屋后有一棵桃树,他调皮的孙子每天从树上摘下一些桃子和邻居的小伙伴分吃。第一天摘下桃子总个数的,以后的8天分别摘下当天现有桃子的、、…、,摘了9天,树上还留下10个桃子。树上原来有多少个桃子?
(2022·广东潮州·统考小升初真题)
57.东风机械厂有两个车间,甲车间人数是乙车间人数的,如果从乙车间调18人到甲车间,则两个车间人数相等,甲、乙两个车间原来各有多少人?
试卷第10页,共11页
试卷第1页,共11页
参考答案:
1.购票50张;3400元
【分析】方法一:购买46张门票,46<50,没有优惠,用85元乘上46人就是全部的钱数;
方法二:购买50张门票,可以按照8折优惠,先求出50张门票的原价,然后再乘上80%,就是需要的钱数;
比较两种方法需要的钱数即可求解。
【详解】46×85=3910(元)
50×85×80%
=50×85×0.8
=3400(元)
3910>3400
答:购票50张花钱最少,最少要用3400元。
【点睛】如果人数少于50时,只有当人数比较接近于50人时,这种方案才省钱,如果和50人相差人数达到一定数值就不省钱了。
2.600元
【分析】把原价看作单位“1”,现价九折出售,就是按原价的90%出售,即便宜了(1-90%),根据求一个数的百分之几是多少,用乘法计算。
【详解】
(元)
答:便宜了600元。
【点睛】解答本题的关键是找出单位“1”,已知单位“1”的量求它的百分之几是多少用乘法计算。
3.500支
【分析】根据题意可知,“下午接种疫苗支数×(1+20%)=上午接种疫苗支数”,据此求出下午为人民群众接种新冠肺炎疫苗的支数即可。
【详解】600÷(1+20%)
=600÷1.2
=500(支)
答:下午为人民群众接种新冠肺炎疫苗500支。
【点睛】明确百分数除法的意义是解答本题的关键。
4.含氢0.7千克,含氧5.6千克
【分析】用水的总量除以总份数求出每份是多少千克,再乘氢和氧各自占的份数即可。
【详解】6.3÷(1+8)
=6.3÷9
=0.7(千克);
0.7×1=0.7(千克);
0.7×8=5.6(千克);
答:6.3的水含氢0.7千克,含氧5.6千克。
【点睛】先求出每份是多少千克是解答本题的关键。
5.550千米
【分析】已知比例尺和图上距离求实际距离,根据“图上距离÷比例尺=实际距离”求出广州到北京两地间的实际距离;一架飞机从广州飞往北京,飞行时间是4小时,再根据“路程÷时间=速度”列式解答。
【详解】4.4÷=220000000(厘米)=2200(千米)
2200÷4=550(千米)
答:这架飞机平均每小时飞行550千米。
【点睛】熟练运用比例尺、图上距离、实际距离三者间的关系,注意计算过程中单位的转化。
6.男生有20人,女生有25人
【分析】设女生的人数有x人,则男生有x人,根据男生人数+女生人数=45,据此列方程解答即可。
【详解】解:设女生的人数有x人,则男生有x人。
x+x=45
x=45
x=25
25×=20(人)
答:合唱队里男生有20人,女生有25人。
【点睛】本题考查用方程解决问题,明确数量关系是解题的关键。
7.(1)60件;
(2)50件
【分析】(1)把六(1)班提交作品的数量看作单位“1”,六(2)班提交作品的数量占六(1)班的(1+),最后用乘法求出六(2)班提交作品的数量;
(2)根据六(2)班提交作品的数量求出比中每份的量,再乘六(3)班提交作品的数量占的份数,据此解答。
【详解】(1)48×(1+)
=48×
=60(件)
答:六(2)班提交了60件作品。
(2)60÷6×5
=10×5
=50(件)
答:六(3)班提交了50件作品。
【点睛】已知一个数,求比这个数多(少)几分之几的数是多少用乘法计算。
8.作图见详解; 168千米。
【分析】用一条线段表示杭州到上海的全程,求全程在线段图上用问号表示,找到线段的中点,即全程的处,中点往右一段表示16.8千米,据此作图。根据线段图,将全程看作单位“1”,已经行了全程的,超过中点(),超过的距离÷对应分率=全程,据此列式解答。
【详解】
16.8÷()
=16.8÷
=168(千米)
答∶杭州到上海高铁路线全程168千米。
【点睛】关键是确定单位“1”,理解分数除法的意义,部分数量÷对应分率=整体数量。
9.(1)87.92平方厘米;(2)87.92平方厘米。
【分析】(1)根据圆柱表面积=底面积×2+侧面积,列式解答即可。
(2)根据圆柱体积=底面积×高,求出橡皮泥体积,再根据圆锥的底面积=体积×3÷高,列式解答即可。
【详解】(1)3.14×22×2+2×3.14×2×5
=3.14×4×2+2×3.14×2×5
=25.12+62.8
=87.92(平方厘米)
答∶这个橡皮泥的表面积是87.92平方厘米。
(2)3.14×22×5
=3.14×4×5
=62.8(立方厘米)
62.8×3÷5=37.68(平方厘米)
答∶这个橡皮泥的底面积是87.92平方厘米。
【点睛】关键是掌握圆柱表面积公式,掌握并灵活运用圆柱和圆锥的体积公式。
10.8厘米
【分析】根据题干分析可得,可设两个容器的水深相同为x厘米,则容器A中的水的体积是:40×30×x立方厘米;容器B中的水的体积是30×20×x立方厘米,根据两个容器内水的体积之和等于B容器中高为24厘米时的水的体积,即可列出方程,求出x的值即可解答问题。
【详解】解:设两个容器的水深相同为x厘米,根据题意可得方程:
40×30×x+30×20×x=30×20×24
1200x+600x=14400
1800x=14400
x=8
答:这时两个容器水深是8厘米。
【点睛】此题考查了长方体的容积公式的计算应用,抓住水的体积不变列出方程解决问题。
11.1266元
【分析】利息=本金×年利率×时间,据此解答。
【详解】6000×4.22%×5
=253.2×5
=1266(元)
答:到期后她可以捐出1266元。
【点睛】此题考查的目的是理解利息的意义,掌握利息的计算方法及应用。
12.135.02平方米
【分析】求贴瓷砖的面积就是求圆柱的一个底面积和一个侧面积的和,利用S表=πr2+2πrh计算解答。
【详解】3.14×10×1.8+3.14×(10÷2)2
=31.4×1.8+3.14×25
=56.52+78.5
=135.02(平方米)
答:这个水池贴瓷砖的面积是135.02平方米。
【点睛】此题主要考查圆柱体的表面积,解答时一定要注意分清题目中的条件,灵活解答。
13.455.3平方厘米
【分析】由图可知,笔筒是无盖的,求需要多少平方厘米的卡纸,只要求出圆柱的侧面积和一个底面积即可,利用公式,代入数据进行解答即可。
【详解】3.14×10×12+3.14×(10÷2)2
=3.14×120+3.14×25
=376.8+78.5
=455.3(平方厘米)
答:至少需要455.3平方厘米的卡纸。
【点睛】此题主要考查了圆柱体的表面积的意义及在生活中的实际应用。
14.90千米/时
【分析】根据“实际距离=图上距离÷比例尺”求出两城市之间的实际距离,再根据“总路程÷相遇时间=速度和”求出客、货车的速度和,最后用速度和减去货车的速度即可。
【详解】2.7÷=81000000(厘米)
81000000厘米=810千米
810÷5-72
=162-72
=90(千米/时)
答:客车的速度是90千米/时。
【点睛】根据比例尺和图上距离求出实际距离是解答题目的关键。
15.125.6米
【分析】先根据圆锥的体积公式求得圆锥形沙堆的体积;再将路面看作一个长方体,它的体积等于圆锥形沙堆的体积,根据长方体的体积公式可求能铺路面的长度。
【详解】2厘米=0.02米
×31.4×2.4÷(10×0.02)
=×75.36÷0.2
=25.12÷0.2
=125.6(米)
答:能铺125.6米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
16.63元
【分析】把这套运动服的价格看作单位“1”,裤子的价格占这套运动服价格的,根据这套运动服的价格用乘法求出裤子的价格,据此解答。
【详解】144×
=144×
=63(元)
答:裤子的价格是63元。
【点睛】掌握按比例分配问题的解题方法是解答题目的关键。
17.10597.5千克
【分析】根据圆柱的体积公式,先列式计算出粮囤的体积,再将体积乘每立方米玉米的重量750千克,求出这个粮囤能装多少千克玉米。
【详解】3.14×1.52×2×750
=14.13×750
=10597.5(千克)
答:这个粮囤能装10597.5千克玉米。
【点睛】本题考查了圆柱的体积,圆柱的体积=底面积×高。
18.到汇集超市购买较合算,理由见详解
【分析】本题可根据学校要购买水杯的数量及两个商家优惠方案分别进行分析计算即能得出到哪家比较合算。
【详解】九折=90%
4×160×90%
=640×90%
=576(元)
160÷8=20(只)
(160-20)×4
=140×4
=560(元)
576>560
答:到汇集超市购买较合算。
【点睛】解决本题关键是分清楚两个超市不同的优惠方法,找出计算现价的方法,从而得解。
19.120千米
【分析】根据题意,这道题的等量关系是:去时的速度×时间=返回时的速度×时间,根据这个等量关系代入数据,列方程解答。
【详解】解:设原来每小时行x千米。
6x=(x-5)×8
6x=8x-40
6x+40=8x-40+40
6x+40=8x
8x-6x=6x+40-6x
2x=40
2x÷2=40÷2
x=20
20×6=120(千米)
答:甲城到乙城的路程有120千米。
【点睛】本题考查行程问题的解题方法,用方程解答比较简便,解题关键是找出题目中的等量关系,列方程解答。
20.273.6平方米
【分析】龙井柱是圆柱形,刷漆的部分是侧面积,侧面积=底面周长×高,根据公式先求出一个龙井柱的侧面积,再乘4就是四根龙井柱刷漆的总面积,据此解答。
【详解】3×1.2×19×4
=3.6×19×4
=273.6(平方米)
答:刷漆面积共是273.6平方米。
【点睛】此题主要考查了圆柱侧面积的相关应用,注意从题目中提取有效数学信息。
21.10时
【分析】根据实际距离=图上距离÷比例尺,据此求出深圳福田站到北京西站的实际距离,再除以动车的速度即可。
【详解】60÷ =240000000(厘米)
240000000厘米=2400千米
2400÷225=10 (时)
答:G72动车从福田站运行到北京西站大约需要10时。
【点睛】此题主要考查了图上距离和实际距离的换算,换算单位时注意数清0的个数。
22.185厘米
【分析】把“火星1号”高度看作单位“1”,“火星1号”高度×+1=“祝融号”高度,据此解答。
【详解】230×+1
=184+1
=185(厘米)
答:“祝融号”高185厘米。
【点睛】此题主要考查了分数乘法的应用,明确求一个数的几分之几用乘法。
23.(1)300
(2)见详解
【分析】(1)根据已知一个数的百分之几是多少,求这个数,根据扇形统计图和条形统计图提供的信息,150÷50%,就是共调查的人数;
(2)求出D的人数,用总人数-A的人数-B 的人数-C的人数,在补充条形统计图。
【详解】(1)150÷50%=300(人)
(2)300-30-150-90
=270-150-90
=120-90
=30(人)
【点睛】本题考查扇形统计图和条形统计图的应用,根据统计图提供的信息,解答问题。
24.195.936g
【分析】根据圆锥体积公式V=Sh,求出铅锤体积,用体积×每立方厘米重量=铅锤总重量。
【详解】×3.14×2 ×6×7.8
=25.12×7.8
=195.936(克)
答:这个铅锤重195.936g。
【点睛】本题主要考查了圆锥体积,圆锥体积=×底面积×高。
25.(1)复式折线
(2)
(3)30
(4) 陈莉 善于阅读和反思,自制力较强
【分析】(1)图中有两条折线,所以这是一幅复式折线统计图;
(2)李明同学第一次的成绩是80分,第五次练习成绩是92分,比的前项是80,比的后项是92,根据求比值的方法计算;
(3)先求出陈莉第五次的成绩比第一次高多少分,把第一次的成绩看作单位“1”,再根据A比B多百分之几的计算方法:(A-B)÷B×100%求出结果;
(4)通过观察统计图可知,陈莉的成绩提高得更快,主要原因可能是陈莉同学善于阅读和反思,自制力比较强(答案不唯一)。
【详解】(1)这是一幅复式折线统计图。
(2)80∶92
=80÷92
=
所以,李明同学第一次与第五次练习成绩比的比值是。
(3)(91-70)÷70×100%
=21÷70×100%
=0.3×100%
=30%
所以,陈莉同学第五次比第一次练习成绩提高了30%。
(4)由折线统计图可知,陈莉的成绩提高得更快,主要原因可能是陈莉同学善于阅读和反思,自制力较强(答案不唯一)。
【点睛】理解复式折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
26.26次
【分析】根据“圆锥形石子堆的底面周长是25.12米”,先求出石子堆的底面半径,然后求出石子堆的体积,进一步求出石子堆的重量,进而问题得解。
【详解】石子堆的底面半径:25.12÷3.14÷2=4(米)
石子堆的体积:3.14×42×3×=50.24(立方米)
石子的重量:50.24×2=100.48(吨)
要运的次数:100.48÷4≈26(次)
答:要运26次才能运完。
【点睛】先求出石子堆的总重量是解决本题的关键。
27.240页
【分析】把全书总页数看作单位“1”,求全书总页数用没读的64页除以它对应的分率,第一天读了总页数的,第二天读了总页数的的,用1减去两天已读的分率,就是没读页数的分率,据此可解。
【详解】64÷(1--×)
=64÷(-)
=64÷
=240(页)
答:全书共有240页。
【点睛】此题重点考查解决求单位“1”的量的分数问题的方法,解答时用数量除以对应的分率。
28.70块
【详解】解:设如果改用边长6分米的正方形方砖铺地,需要x块.
6×6×x=9×280
36x=2520
x=70
答:如果改用边长6分米的正方形方砖铺地,需要70块。
29.300千克
【分析】把10吨海水可以晒海盐的质量设为未知数,盐的质量÷海水的质量×100%=含盐率(一定),比值一定,海水的千克数和盐的千克数成正比例关系,据此解答。
【详解】10吨=10000千克
解:设10000千克海水可以晒x千克海盐。
15∶500=x∶10000
500x=150000
x=150000÷500
x=300
答:10吨海水可以晒300千克海盐。
【点睛】先判断题中的两种相关联的量成什么比例,并找准对应量是解答题目的关键。
30.1.2小时
【分析】比例尺表示图上距离1cm,实际距离50km。甲、乙两地之间的距离是12厘米,那么实际距离就是12×50=600(km),再根据时间=路程÷速度,计算即可。
【详解】12×50=600(km)
600÷500=1.2(小时)
答:飞到乙地需要1.2小时。
【点睛】此题的关键是先求出甲、乙两地之间的距离,然后再进一步解答。
31.113.04 dm2
【分析】订做的圆柱体铁皮水桶所需的铁皮就是这个圆柱的侧面积加上底面圆的面积,可根据圆柱体的表面积公式:侧面积+底面积;因为这个圆柱体铁通是无盖的,所以只需一个底面积,据此可得出答案。
【详解】底面直径为:(dm),则半径就为2dm,故做这个水桶至少要用铁皮:
=113.04(dm2)
答:做这个水桶至少要用113.04 dm2铁皮。
【点睛】本题主要考查的是圆柱的表面积实际运用,解题时需要注意这个圆柱体铁桶是无盖的,计算时只能计算一个底面圆面积。
32.(1)144元、160元
(2)A商场
【分析】(1)A商场:用标价乘折扣即可求出实际的价格;B商场240元里面有2个100元,可以减去80元,用标价减去优惠掉的80元即为实际的价格;
(2)将两家商场需要的钱数比较即可。
【详解】(1)A商场:六折=60%
240×60%=144(元)
B商场:240÷100=2(个)……40(元)
240-40×2
=240-80
=160(元)
答:在A、B两个商场买各应付144元和160元。
(2)144<160
答:A商场更省钱。
【点睛】理解两家商场的优惠方式是解答本题的关键。
33.80吨
【分析】圆锥的体积=底面积×高×,先计算圆锥的体积,再乘每立方米沙的重量,即可求出这堆沙的总重量。
【详解】3.14×52×1.8××1.7
=3.14×15×1.7
=3.14×25.5
≈80(吨)
答:这堆沙约重80吨。
【点睛】此题考查如何利用圆锥的体积公式进行实际应用,计算结果要用“四舍五入”法。
34.2分球:6个;3分球:2个
【详解】假设投中的全部是2分球,可得:2×8=16(分),比实际得的18分少:18-16=2(分),是因为我们把每个2分球当作了3分球,每个球多算了3-2=1(分),所以可以求出3分球的个数:2÷1=2(个);再进一步解答即可。
【解答】假设投中的全部是2分球:
(18-2×8)÷(3-2)
=2÷1
=2(个)
8-2=6(个)
答:他投进2分球6个,3分球2个。
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法进行分析比较,进而得出结论;也可以用方程,设其中的一个数为未知数,另一个数也用未知数表示,列出方程解答即可。
35.180÷(-35%)=1200(kg)
【详解】略
36.48页
【分析】根据乘数的意义,第一天看的页数=全书的页数×;第二天看的页数=余下的页数×;余下的页数=全书页数-第一天看的页数;第一天的页数+第二天的页数=两天一共看的页数。
【详解】120×+(120-120×)×
=24+(120-24)×
=24+96×
=24+24
=48(页)
答:两天一共看了48页。
【点睛】分析题目数量之间的关系,根据数量之间的关系列出数量关系式,根据数量关系式解决问题。
37.10%
【分析】通常把“比”后的量看作单位“1”,把第一季度的营业额看作单位“1”。用两季度营业额之差除以第一季度的营业额,即可求出第二季度的营业额比第一季度增长了百分之几。
【详解】(16.5-15)÷15
=1.5÷15
=10%
答:第二季度的营业额比第一季度增长了10%。
【点睛】求一个数比另一个数多/少百分之几,用两数之差除以另一个数。
38.(1)见详解;
(2)16
【分析】(1)将三角形按2∶1的比放大,则放大后的边长为原来边长的2倍,据此画出放大后的图形即可;
(2)根据“s=ah÷2”求出放大后的图形的面积即可。
【详解】(1)如图:
(2)8×4÷2=16(平方厘米)
【点睛】熟练掌握图形放大与缩小的方法是解答本题的关键。
39.14.5米
【分析】同一时间,同一地点测得物体与影子的比值相等,它们成正比例关系,也就是米尺的长度与影子的比等于树的高与影子的比,设这棵老树的高为x米,组成比例,解比例即可。
【详解】解:设这棵老树的高为x米。
x∶8.7=1∶0.6
0.6x=8.7×1
0.6x=8.7
x=14.5
答:这棵老树的高度是14.5米。
【点睛】解答此题的关键是,判断实际高度与影子成正比例,由此列出比例解决问题。
40.(1)100.48平方分米;
(2)35升
【分析】(1)将数据代入到圆柱的表面积公式:S=中计算即可。
(2)将数据代入到圆柱的容积公式:V=中计算即可。
【详解】(1)3.14×(4÷2)2×2+3.14×4×6
=3.14×22×2+12.56×6
=3.14×4×2+75.36
=25.12+75.36
=100.48(平方分米)
答:外壳的表面积是100.48平方分米。
(2)3.14×(3÷2)2×5
=3.14×1.52×5
=3.14×2.25×5
=3.14×11.25
≈35(立方分米)
35立方分米=35升
答:内胆的容积约是35升。
【点睛】本题主要考查圆柱的表面积、容积公式的实际应用。
41.(1)80人;(2)图见详解;(3)25%
【分析】(1)总人数=美术人数÷美术人数所占百分率;
(2)足球人数=总人数×足球人数所占百分率,据此补全条形统计图;
(3)用演讲人数与足球人数之差除以演讲人数即可。
【详解】(1)10÷12.5%=80(人)
答:抽样调查总人数有80人。
(2)80×18.75%=15(人)
作图如下:
(3)(20-15)÷20
=5÷20
=25%
答:“足球”的人数比“演讲”的人数少25%。
【点睛】此题考查条形统计图和扇形统计图的综合应用,能够从统计图中提取有效数学信息是解题关键。
42.(1);
上午8:00到上午11:00行驶了3小时,行驶了300千米,图上距离是6厘米
(2)不需要
(3)12点40分
【分析】(1)上午8:00到上午11:00行驶了3小时,小车的速度×行驶的时间求出行驶的路程,根据实际距离×比例尺=图上距离,求出上午11:00时小车行驶的图上距离,据此作图;
(2)根据图上距离÷比例尺=实际距离求出甲地到乙地的实际距离,再除以100千米求出有多少个100,再乘以8升求出消耗的汽油,最后再与出发时油箱里的油比较;
(3)原来小车的速度×(1-10%)求出现在小车的速度,甲地到乙地的距离-上午11:00前行驶的路程求出剩下的路程,再除以现在小车的平均速度求出还需要行驶的时间,上午11:00加上还需要行驶的时间即为李老师到达乙地的最早时间。
【详解】(1)11:00-8:00=3(小时)
100×3=300(千米)=30000000(厘米)
30000000×=6(厘米)
作图如下:
(2)9÷=45000000(厘米)=450(千米)
450÷100×8
=4.5×8
=36(升)
36升<40升
答:中途不需要再加油。
(3)100×(1-10%)
=100×90%
=90(千米)
(450-300)÷90
=150÷90
=1(小时)
1=1小时40分
11:00+1小时40分=12:40
答:李老师到达乙地的最早时间是12点40分。
【点睛】掌握图上距离、实际距离、比例尺之间的关系是解答此题的关键。
43.11.775立方厘米
【分析】看图可知,圆锥底面直径是3厘米,高是5厘米,根据圆锥体积=底面积×高÷3,列式解答即可。
【详解】3.14×(3÷2) ×5÷3
=3.14×2.25×5÷3
=11.775(立方厘米)
答:这个零件的体积是11.775立方厘米。
【点睛】关键是通过观察确定圆锥的底面直径和高。
44.(1)20平方分米
(2)0.6立方分米
【分析】(1)正方体玻璃容器(无盖),则玻璃的面积应是5个面的面积;
(2)土豆的体积等于水面上升部分的体积,用水与土豆的体积之和减去水的体积得到土豆的体积。
【详解】(1)2×2×5
=4×5
=20(平方分米)
答:这个玻璃容器至少需要20平方分米的玻璃。
(2)5升=5立方分米
14厘米=1.4分米
2×2×1.4-5
=5.6-5
=0.6(立方分米)
答:土豆的体积是0.6立方分米。
【点睛】本题考查正方体的表面积、求不规则物体的体积,解答本题的关键是掌握求不规则物体的体积的方法。
45.见详解
【分析】(1)求出图1总人数,总人数-乘车感染数-旅游感染数-舍去感染数=聚餐感染数,据此将图2补充完整;
(2)答案不唯一,如2月2日和2月3日两天的感染人数是1月31日感染人数的几倍,求出2月2日和2月3日两天的感染人数和,除以1月31日感染人数即可;
(3)答案不唯一,合理即可。
【详解】(1)5+9+5+6+4+6-8-9-2
=35-19
=16(人)
(2)问题:2月2日和2月3日两天的感染人数是1月31日感染人数的几倍?
列式:(6+4)÷5
(3)减少聚餐,因为聚餐导致的感染人数非常多。
【点睛】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较。
46.(1)56%
(2)499百万件
【分析】(1)用申通快递的业务量除以韵达快递业务量,再乘100%,其结果百分号前保留整数即可;
(2)根据已知比一个数多百分之几的数是多少,求这个数,用除法解答即可。
【详解】(1)390÷701×100%
≈0.56×100%
=56%
答:2021年2月,申通快递的业务量是韵达快递业务量的56%。
(2)699÷(1+40%)
=699÷1.4
≈499(百万件)
答:顺丰快递2020年2月的快递业务量约是499百万件。
【点睛】本题考查求一个数占另一个数的百分之几,明确用除法是解题的关键。
47.2.25小时
【分析】根据路程一定,速度与时间成反比例,由此列出比例解答即可。
【详解】解:设x小时可回到出发地。
3.2x=3.6×2
3.2x=7.2
3.2x÷3.2=7.2÷3.2
x=2.25
答:2.25小时可回到出发地。
【点睛】解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;再列出比例解答即可。
48.(1)44平方分米;(2)18.84升
【分析】(1)一个水桶需要的铁皮的面积=水桶的侧面积+底面积,利用圆柱的侧面积和圆的面积公式即可得解,得数再乘2即可;
(2)先根据圆柱的容积V=πr2h,求出一个水桶的容积,再乘2就是一对水桶的容积。
【详解】(1)3.14×20×30+3.14×(20÷2)2
=1884+314
=2198(平方厘米)
2198×2=4396(平方厘米)
4396平方厘米≈44平方分米
答:做这样一对水桶大约需要44平方分米铁皮。
(2)3.14×(20÷2)2×30
=3.14×100×30
=9420(立方厘米)
9420立方厘米=9.42升
9.42×2=18.84(升)
答:这对水桶可以装水18.84升。
【点睛】此题主要考查圆柱的表面积和圆柱的体积的计算方法,要记住求的是一对水桶需要的铁皮的面积和容积。
49.5公顷
【分析】根据题意,把果园的总面积看作单位“1”,已知种桃树和李子树的总面积与种樱桃树的面积的比是7∶5,那么种桃树和李子树的总面积就占果园总面积的,种樱桃树的面积就占果园总面积的,种李子树的面积就占果园总面积的(-),它对应的面积是2.5公顷,据此用除法计算求出果园总面积,再乘种樱桃树的面积所占的分率即可求出种樱桃树的面积是多少公顷。
【详解】2.5÷(-)×
=2.5÷×
=5(公顷)
答:种樱桃树的面积是5公顷。
【点睛】本题主要考查比的实际应用,解答本题的关键是求出三种果树种植面积各自占果园总面积的分率。
50.乙商场
【分析】分析题意,甲商场购物满300元返现金40元,将皮鞋的价钱与40元相减,计算得出淘气妈妈在甲商场实际付出的钱数;乙商场所有商品一律八五折出售,将皮鞋的价钱与85%相乘,计算得出淘气妈妈在乙商场实际付出的钱数,不难解答本题。
【详解】400-40=360(元)
400×85%=340(元)
340<360
答:淘气妈妈到乙商场购买更优惠。
【点睛】本题是一道折扣问题,需结合折扣问题中的数量关系,求一个数的百分之几的知识进行求解。
51.30立方米
【分析】先利用圆锥的体积V=Sh,求出这些谷子的体积,进而利用已知一个数的几百分之几是多少,求这个数,用除法计算的方法,即可求出这个粮仓的容积。
【详解】18分米=1.8米
×10×1.8÷20%
=6÷20%
=30(立方米)
答:这个粮仓的容积是30立方米。
【点睛】此题主要考查圆锥的体积的计算方法在实际中的应用。
52.20千克
【分析】先把甲袋大米的质量看作单位“1”,取出后,再剩下(1-),根据分数乘法的意义,即可求出此时甲袋所剩大米的质量。再把甲袋所剩大米的质量平均分成8份,先用除法求出1份的质量,再用乘法求出3份的质量,即乙袋取出25%后剩大米的质量。再把乙袋原来大米的质量看作单位“1”,根据百分数除法的意义,用乙袋所剩大米的质量除以(1-25%),就是乙袋大米原来的质量。
【详解】60×(1-)÷8×3÷(1-25%)
=60×÷8×3÷75%
=20(千克)
答:乙袋中原来有20千克大米。
【点睛】关键是根据分数乘法的意义,求出甲袋取出后剩下的质量。除按上述解答方法外,也可把比转化成分数,求出乙袋取出25%后剩的质量,然后再根据百分数除法的意义,求乙袋原来的质量。
53.(1)32立方米(2)30立方米
【分析】(1)用乐乐家六月末水表读数减去五月末水表读数就是乐乐家六月份的用水量。
(2)根据阶梯收费的方法逐步求出a的值。
【详解】(1)143-111=32(立方米)
答:六月份共用了32立方米水。
(2)将32立方米水的收费进行分级:
第一级:用水量20立方米,用水费:20×1.74=34.8(元)
剩余的12立方米水,共交水费:68.58-34.8=33.78(元)
(33.78-2.61×12)÷(3.84-2.61)
=2.46÷1.23
=2(立方米)
12-2=10(立方米)
按第三级收费的有2立方米,则按第二级收费的10立方米。
20+10=30(立方米)
答:当用水30立方米以上时收费标准是3.84元/立方米。
【点睛】本题考查了阶梯收费问题,难度较大,需认真分析题目中的数量关系。
54.(1)490千米
(2)小时
【详解】(1)196÷(80%+-1)
=196÷
=490(千米)
答:全程是490千米。
(2)客车与货车的速度比是: ∶80%=3∶4
相遇时货车行的路程为:490×=280(千米)
货车的速度为:280÷5=56(千米/小时)
490÷56=(小时)
答:货车行完全程需要小时。
55.够
【分析】根据利息=本金×时间×利率,求出到期时小芳的利息,因为银行的利息税是5%,所以实得利息为所得利息的(1-5%),根据乘法的意义,求出实得利息。书包的售价=原价×85%,与实得利息比较即可。
【详解】500×2×4.50%×(1-5%)
=45×95%
=42.75(元);
50×85%=42.5(元)
42.75>42.5
答:钱够。
【点睛】此题考查属于百分数的综合性题目,关键是求出实得利息与书包的售价。明确求一个数的百分之几是多少用乘法。
56.100个
【分析】根据题意,把当天桃子总数看作单位“1”,则第9天摘之前树上的桃子数是10÷(1-),同理,第8天摘之前树上的桃子是第9天桃子总数(第8天剩下的桃子数)的(1-),依此类推,用除法求出桃子总数即可。
【详解】10÷(1-)÷(1-)÷…÷(1-)
=10÷÷…
=10×2××…×
=10×10
=100(个)
答:树上原来有100个桃子。
【点睛】本题主要考查逆推问题,关键求摘之前树上桃子的数量。
57.甲车间原来有60人,乙车间原来有96人
【分析】把乙车间原来的人数看作单位“1”,由题意可知,乙车间比甲车间多2个18人,即(18×2)人,这(18×2)人正好是乙车间人数的(1-),根据分数除法的意义,用(18×2)人除以(1-),就是乙车间原来的人数。再根据分数乘法的意义,用乙车间原来的人数乘,就是甲车间原来的人数。
【详解】18×2÷(1-)
=36÷
=96(人)
96×=60(人)
答:甲车间原来有60人,乙车间原来有96人。
【点睛】此题是考查分数乘、除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
答案第4页,共25页
答案第3页,共25页
广东省各地区近两年小升初真题题型汇编专项训练
一、解答题。
(2022·广东梅州·统考小升初真题)
1.全班46人去客天下游览。门口的购票须知上写着:门票每人85元50人开始可以享受八折优惠。你认为怎样购票花钱最少,最少要用多少钱?
(2022·广东汕头·统考小升初真题)
2.“五一”商场举行促销活动,一款双开门冰箱原标价6000元,现价九折出售,便宜了多少元?
(2021·广东广州·统考小升初真题)
3.接种新冠肺炎疫苗是“外防输入,内防反弹”的必要举措。某社区卫生服务中心某天上午为人民群众免费接种新冠肺炎疫苗600支,比下午多接种20%。下午为人民群众接种新冠肺炎疫苗多少支?
(2021·广东汕尾·统考小升初真题)
4.水是由氢和氧按1∶8的质量比化合而成的。6.3的水含氢和氧各多少?
(2022·广东韶关·统考小升初真题)
5.在比例尺1∶50000000的地图上,量得广州到北京的距离是4.4厘米,一架飞机从广州飞往北京,4小时到达。这架飞机平均每小时飞行多少千米?
(2022·广东江门·统考小升初真题)
6.学校合唱队共有45位同学,其中男生的人数是女生的,合唱队里男生和女生各有多少人?(列方程解答)
(2022·广东广州·统考小升初真题)
7.学校举行六年级美术作品征集比赛。六(1)班提交了48件作品,六(2)班提交的作品比六(1)班多,六(3)班和六(2)班提交的作品件数比是5∶6。
(1)六(2)班提交了多少件作品?
(2)六(3)班提交了多少件作品?
(2022·广东广州·统考小升初真题)
8.一列高铁从杭州开往上海,已经行了全程的,恰好距离中点16.8千米处。杭州到上海高铁路线全程多少千米?先把线段图补充完整(请在线段图中标出“16.8千米”和要求的问题。)并解答。
(2022·广东广州·统考小升初真题)
9.一个圆柱形橡皮泥,底面半径是2厘米,高是5厘米。
(1)这个橡皮泥的表面积是多少平方厘米?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
(2022·广东梅州·统考小升初真题)
10.现有空的长方体容器A和水深24厘米的长方体容器B(如图),要将容器B的水倒一部分给A,使两容器水的高度相同,这时水深是几厘米?
(2022·广东阳江·统考小升初真题)
11.王大妈把6000元存入银行,定期5年,准备到期后把利息捐赠给福利院。如果年利率按4.22%计算,到期后她可以捐出多少元?
(2022·广东阳江·统考小升初真题)
12.有一个底面直径10米,高1.8米圆柱形水池,如果在水池内壁和底面都要贴上瓷砖,这个水池贴瓷砖的面积是多少平方米?
(2022·广东珠海·统考小升初真题)
13.芳芳用卡纸制作了一个底面直径是10厘米,高12厘米的笔筒,至少需要多少平方厘米的卡纸?
(2022·广东珠海·统考小升初真题)
14.在一幅比例尺是1∶30000000的地图上,量得两城市之间的距离是2.7厘米,一列货车和一列客车分别从两地同时相对开出,5小时后相遇。货车的速度是72千米/时,客车的速度是多少?
(2022·广东珠海·统考小升初真题)
15.一个圆锥形沙堆,底面积是31.4平方米,高是2.4米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
(2022·广东汕头·统考小升初真题)
16.一套运动服的价格是144元,裤子和上衣价格的比是7∶9,裤子的价格是多少元?
(2022·广东汕头·统考小升初真题)
17.一个圆柱形粮囤,从里面量得底面半径是1.5米,高2米。如果每立方米玉米约重750千克,这个粮囤能装多少千克玉米?
(2021·广东广州·统考小升初真题)
18.为了学生的卫生安全,学校给每个学生配一个水杯,每只水杯4元,美好家园打九折,汇集超市“买七送一”。学校想买160只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
(2021·广东广州·统考小升初真题)
19.一辆汽车从甲城开往乙城6小时到达,返回时减慢了速度,每小时比原来少行5千米,结果用了8小时就回到了甲城,求甲城到乙城的路程有多少千米?
(2021·广东深圳·统考小升初真题)
20.建于明永乐十八年(1420)的北京天坛祈年殿已有600年历史。祈年殿为砖木结构,殿高约38米,底层直径约32米,三层重檐向上逐层收缩作伞状。殿内有28根金丝楠木大柱,内围的4根“龙井柱”象征春、夏、秋、冬四季,每根高约19米,直径1.2米。如果要给这4根“龙井柱”刷上油漆,则刷漆面积共是多少平方米?(本题π值取3)
(2021·广东深圳·统考小升初真题)
21.在比例尺是1∶4000000的交通地图上,量得深圳福田站到北京西站的长度约60厘米。从福田站开往北京西站的G72动车每小时约行225千米,G72动车从福田站运行到北京西站大约需要多少时间?(不考虑列车途中靠站停留等因素)
(2021·广东深圳·统考小升初真题)
22.我国首次火星探测即实现着陆(2021年5月15日)的“祝融号”火星车高度是苏联的火星探测器“火星1号”(未着陆成功)的多1厘米,“火星1号”高230厘米。“祝融号”高多少厘米?
(2021·广东深圳·统考小升初真题)
23.联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,环保小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将结果分析整理制作成了下面两个统计图。其中:
A是能将垃圾放在规定的地方,而且还会考虑垃圾的分类
B是能将垃圾放在规定的地方,但不会考虑垃圾的分类。
C是偶尔会将垃圾放在规定的地方。
D是随手乱扔垃圾。
根据以上信息回答问题。
(1)该校环保小组共调查了( )人。
(2)请补全条形统计图。
(2021·广东阳江·统考小升初真题)
24.建筑工人使用一个圆锥形的铅锤来判断建筑物是否垂直,这个铅锤底面半径2cm,高6cm,每立方厘米铅锤约重7.8g,这个铅锤重多少g?
(2021·广东阳江·统考小升初真题)
25.在抗击新冠肺炎期间,甲和乙两位同学按照“停课不停学”要求,合理安排时间并进行阶段练习。(如图)
(1)这是一幅( )统计图。
(2)李明同学第一次与第五次练习成绩比的比值是( )。
(3)陈莉同学第五次比第一次练习成绩提高了( )%。
(4)从统计图中,可以直接看出( )同学的成绩提高得更快,主要原因可能是:( )。
(2021·广东肇庆·统考小升初真题)
26.一个圆锥形石子堆,底面周长25.12米,高3米,每立方米石子重2吨,如果用一辆载重4吨的汽车运,要运多少次才能运完?
(2021·广东肇庆·统考小升初真题)
27.小明读一本书。第一天读了总页数的,第二天读的页数是第一天读的页数的,还剩64页没有读。全书共有多少页?
(2021·广东河源·统考小升初真题)
28.一个房间,用面积9平方分米的方砖铺地,需要280块.如果改用边长6分米的正方形方砖铺地,需要多少块?(用比例知识解)
(2021·广东河源·统考小升初真题)
29.用500kg海水可以晒15kg海盐,照这样计算,用10吨海水可以晒多少kg海盐?(用比例的方法解答)
(2021·广东河源·统考小升初真题)
30.在一幅比例尺是的地图上,量得甲、乙两地之间的距离是12厘米,有一架飞机从甲地飞往乙地,每时飞500千米,飞到乙地需要几时?
(2021·广东广州·统考小升初真题)
31.每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。吴芳家为了节约用水,订做了一个圆柱形铁皮水桶(无盖)蓄水,高8dm,底面直径是高的。做这个水桶至少要用多少铁皮?
(2021·广东广州·统考小升初真题)
32.“六一”儿童节前夕,某品牌的玩具搞促销活动。在A商场打六折出售,在B商场按“每满100元减40元”的方式销售。妈妈要买一个标价240元的这种品牌的玩具。
(1)在A、B两个商场买各应付多少钱?
(2)选择哪个商场更省钱?
(2021·广东广州·统考小升初真题)
33.工地上有一个圆锥形的沙堆,高是1.8米,底面半径是5米,每立方米的沙约重1.7吨。这堆沙约重多少吨?(得数保留整吨)
(2021·广东广州·统考小升初真题)
34.小军在校篮球比赛中,2分球和3分球一共进了8个,共获得18分,小军的2分球和3分球各投进多少个?
(2021·广东广州·统考小升初真题)
35.食堂有一些大米,第一周吃掉了总数的35%,第二周吃掉了180千克,这时剩下的大米与吃掉了的大米一样多.食堂原来有大米多少千克?
(2021·广东广州·统考小升初真题)
36.一本故事书共120页,红红第一天看了,第二天看了余下的,两天一共看了多少页?
(2021·广东汕尾·统考小升初真题)
37.某家电销售第一季度的营业额为15万元,第二季度的营业额为16.5万元。第二季度的营业额比第一季度增长了百分之多少?
(2021·广东汕尾·统考小升初真题)
38.下图中的每小格表示边长1厘米的正方形。
(1)按2∶1的比画出三角形放大后的图形。
(2)放大后三角形的面积是( )平方厘米。
(2021·广东深圳·统考小升初真题)
39.校园内有棵老树长得很高,淘气量出这棵老树的影子长为8.7米,同时在老树的附近竖立一根米尺(长度为1米),量得米尺的影子长为0.6米。这棵老树的高度是多少米?(用比例解答)
(2021·广东深圳·统考小升初真题)
40.笑笑家最近购买了一台电热水器(外壳和内胆均为近似的圆柱体),外壳长为6分米,底面直径为4分米,内胆从里边量长为5分米,底面直径为3分米。
(1)外壳的表面积是多少平方分米?
(2)内胆的容积约是多少升?(结果取整数)
(2021·广东深圳·统考小升初真题)
41.下面是某小学学生参加“430校内课后服务”项目的抽样调查统计图,根据信息完成下面各题。
(1)抽样调查总人数有多少人?
(2)把条形统计图补充完整。
(3)“足球”的人数比“演讲”的人数少百分之几?
(2021·广东深圳·统考小升初真题)
42.在比例尺是1∶5000000的地图上,量得甲地到乙地的图上距离是9厘米。李老师一家上午8:00驾车从甲地前往乙地小车平均每小时行驶100千米。
(1)上午11:00时小车行驶至哪里?请在图中用“”标出,并简要说明理由。
(2)小车每行驶100千米消耗汽油8升,出发时油箱里有40升汽油,中途还需要再加油吗?(写出计算过程)
(3)上午11:00后,由于路上车流量增加,小车的平均速度下降了10%,那么李老师到达乙地的最早时间是几点几分?
(2021·广东东莞·统考小升初真题)
43.一个圆锥形零件,从上面看到的图形如图1,从前面看到的图形如图2(图中每个小正方形的边长表示1cm),这个零件的体积是多少立方厘米?
(2021·广东东莞·统考小升初真题)
44.一个正方体玻璃容器(无盖)的棱长是2分米。
(1)做这个玻璃容器至少需要多少平方分米的玻璃?
(2)向容器中倒入5升水,再把一个土豆没入水中。这时量得容器内水深14厘米。土豆的体积是多少?(玻璃的厚度忽略不计)
(2021·广东东莞·统考小升初真题)
45.2020年新冠肺炎爆发,疫情的蔓延牵动着每个人的心。图1呈现了某地连续7天新增新冠肺炎确诊病例的统计结果,图2是对这些病人发病原因的进一步调查。
(1)请将图2补充完整。
(2)请根据图1提一个需要用除法和加法解决的问题。(提出问题并列出算式,不用计算)
问题:__________________________________________________________________________
列式:__________________________________________________________________________
(3)根据图2,给该地区市民提一条防疫建议,并说明理由。
_________________________________________________________________________________
_________________________________________________________________________________
(2022·广东江门·统考小升初真题)
46.下图是2021年2月四家快递公司业务量。
(1)2021年2月,申通快递的业务量是韵达快递业务量的百分之几?(百分号前保留整数)
(2)顺丰快递2021年2月的业务量比2020年2月增长了40%,顺丰快递2020年2月的快递业务量约是多少百万件?(得数保留整数)
(2022·广东潮州·统考小升初真题)
47.夏令营组织学生行军训练。去时每小时行3.6千米,2小时到达目的地。返程速度减慢一些,每小时行3.2千米,几小时可回到出发地?(用比例知识解答)
(2022·广东潮州·统考小升初真题)
48.一对无盖的圆柱形铁皮水桶,底面直径20厘米,高30厘米。
(1)做这样一对水桶大约需要多少平方分米铁皮?(得数保留整数)
(2)这对水桶可以装水多少升?(铁皮厚度忽略不计)
(2022·广东潮州·统考小升初真题)
49.一个果园,种桃树的面积占果园总面积的,种李子树的面积是2.5公顷,余下的地种樱桃树。已知种桃树和李子树的总面积与种樱桃树的面积的比是7︰5,种樱桃树的面积是多少公顷?
(2022·广东韶关·统考小升初真题)
50.淘气妈妈计划购买一双价值400元的皮鞋,甲乙两个商场优惠活动如下:甲商场凡消费满300元返现金40元;乙商场商品一律打八五折。淘气妈妈到哪个商场购买更优惠?
(2022·广东韶关·统考小升初真题)
51.一个圆锥形稻谷堆,高18分米,占地面积10平方米,把这堆稻谷全部装入一个圆柱形粮仓,正好占整个粮仓的20%,求这个粮仓的容积。
(2022·广东阳江·统考小升初真题)
52.有甲、乙两袋大米,甲袋有60千克,从甲袋取出,从乙袋取出25%后,甲、乙两袋剩余大米的质量比是8∶3。乙袋中原来有多少千克大米?
(2022·广东珠海·统考小升初真题)
53.为鼓励居民节约用水,珠海市规定每户每月用水按阶梯收费,如图:
等级 用水量(立方米) 收费标准(元/立方米)
第一级 20或20以下 1.74
第二级 20以上且a或a以下 2.61
第三级 a以上 3.84
下面是乐乐家近三个月月末的水表读数及交费情况:
月份 四月 五月 六月
月末水表读数(立方米) 86 111 143
本月交水费(元) 31.32 47.85 68.58
(1)乐乐家六月份用水多少立方米?
(2)当用水多少立方米以上时收费标准是3.84元/立方米?
(2021·广东广州·统考小升初真题)
54.客车和货车分别从甲乙两站同时相向开出,5小时后相遇,相遇后两车仍按原速度前进,当他们相距196千米时,客车行了全程的,货车行了全程的80%。
(1)全程是多少千米?
(2)货车行完全程需要多少个小时?
(2021·广东肇庆·统考小升初真题)
55.两年前,小芳将500元压岁钱存入银行,年利率4.50%。今年到期时,小芳准备用实得利息购买下面的书包,钱够不够?(银行利息税5%)
(2021·广东广州·统考小升初真题)
56.王大伯屋后有一棵桃树,他调皮的孙子每天从树上摘下一些桃子和邻居的小伙伴分吃。第一天摘下桃子总个数的,以后的8天分别摘下当天现有桃子的、、…、,摘了9天,树上还留下10个桃子。树上原来有多少个桃子?
(2022·广东潮州·统考小升初真题)
57.东风机械厂有两个车间,甲车间人数是乙车间人数的,如果从乙车间调18人到甲车间,则两个车间人数相等,甲、乙两个车间原来各有多少人?
试卷第10页,共11页
试卷第1页,共11页
参考答案:
1.购票50张;3400元
【分析】方法一:购买46张门票,46<50,没有优惠,用85元乘上46人就是全部的钱数;
方法二:购买50张门票,可以按照8折优惠,先求出50张门票的原价,然后再乘上80%,就是需要的钱数;
比较两种方法需要的钱数即可求解。
【详解】46×85=3910(元)
50×85×80%
=50×85×0.8
=3400(元)
3910>3400
答:购票50张花钱最少,最少要用3400元。
【点睛】如果人数少于50时,只有当人数比较接近于50人时,这种方案才省钱,如果和50人相差人数达到一定数值就不省钱了。
2.600元
【分析】把原价看作单位“1”,现价九折出售,就是按原价的90%出售,即便宜了(1-90%),根据求一个数的百分之几是多少,用乘法计算。
【详解】
(元)
答:便宜了600元。
【点睛】解答本题的关键是找出单位“1”,已知单位“1”的量求它的百分之几是多少用乘法计算。
3.500支
【分析】根据题意可知,“下午接种疫苗支数×(1+20%)=上午接种疫苗支数”,据此求出下午为人民群众接种新冠肺炎疫苗的支数即可。
【详解】600÷(1+20%)
=600÷1.2
=500(支)
答:下午为人民群众接种新冠肺炎疫苗500支。
【点睛】明确百分数除法的意义是解答本题的关键。
4.含氢0.7千克,含氧5.6千克
【分析】用水的总量除以总份数求出每份是多少千克,再乘氢和氧各自占的份数即可。
【详解】6.3÷(1+8)
=6.3÷9
=0.7(千克);
0.7×1=0.7(千克);
0.7×8=5.6(千克);
答:6.3的水含氢0.7千克,含氧5.6千克。
【点睛】先求出每份是多少千克是解答本题的关键。
5.550千米
【分析】已知比例尺和图上距离求实际距离,根据“图上距离÷比例尺=实际距离”求出广州到北京两地间的实际距离;一架飞机从广州飞往北京,飞行时间是4小时,再根据“路程÷时间=速度”列式解答。
【详解】4.4÷=220000000(厘米)=2200(千米)
2200÷4=550(千米)
答:这架飞机平均每小时飞行550千米。
【点睛】熟练运用比例尺、图上距离、实际距离三者间的关系,注意计算过程中单位的转化。
6.男生有20人,女生有25人
【分析】设女生的人数有x人,则男生有x人,根据男生人数+女生人数=45,据此列方程解答即可。
【详解】解:设女生的人数有x人,则男生有x人。
x+x=45
x=45
x=25
25×=20(人)
答:合唱队里男生有20人,女生有25人。
【点睛】本题考查用方程解决问题,明确数量关系是解题的关键。
7.(1)60件;
(2)50件
【分析】(1)把六(1)班提交作品的数量看作单位“1”,六(2)班提交作品的数量占六(1)班的(1+),最后用乘法求出六(2)班提交作品的数量;
(2)根据六(2)班提交作品的数量求出比中每份的量,再乘六(3)班提交作品的数量占的份数,据此解答。
【详解】(1)48×(1+)
=48×
=60(件)
答:六(2)班提交了60件作品。
(2)60÷6×5
=10×5
=50(件)
答:六(3)班提交了50件作品。
【点睛】已知一个数,求比这个数多(少)几分之几的数是多少用乘法计算。
8.作图见详解; 168千米。
【分析】用一条线段表示杭州到上海的全程,求全程在线段图上用问号表示,找到线段的中点,即全程的处,中点往右一段表示16.8千米,据此作图。根据线段图,将全程看作单位“1”,已经行了全程的,超过中点(),超过的距离÷对应分率=全程,据此列式解答。
【详解】
16.8÷()
=16.8÷
=168(千米)
答∶杭州到上海高铁路线全程168千米。
【点睛】关键是确定单位“1”,理解分数除法的意义,部分数量÷对应分率=整体数量。
9.(1)87.92平方厘米;(2)87.92平方厘米。
【分析】(1)根据圆柱表面积=底面积×2+侧面积,列式解答即可。
(2)根据圆柱体积=底面积×高,求出橡皮泥体积,再根据圆锥的底面积=体积×3÷高,列式解答即可。
【详解】(1)3.14×22×2+2×3.14×2×5
=3.14×4×2+2×3.14×2×5
=25.12+62.8
=87.92(平方厘米)
答∶这个橡皮泥的表面积是87.92平方厘米。
(2)3.14×22×5
=3.14×4×5
=62.8(立方厘米)
62.8×3÷5=37.68(平方厘米)
答∶这个橡皮泥的底面积是87.92平方厘米。
【点睛】关键是掌握圆柱表面积公式,掌握并灵活运用圆柱和圆锥的体积公式。
10.8厘米
【分析】根据题干分析可得,可设两个容器的水深相同为x厘米,则容器A中的水的体积是:40×30×x立方厘米;容器B中的水的体积是30×20×x立方厘米,根据两个容器内水的体积之和等于B容器中高为24厘米时的水的体积,即可列出方程,求出x的值即可解答问题。
【详解】解:设两个容器的水深相同为x厘米,根据题意可得方程:
40×30×x+30×20×x=30×20×24
1200x+600x=14400
1800x=14400
x=8
答:这时两个容器水深是8厘米。
【点睛】此题考查了长方体的容积公式的计算应用,抓住水的体积不变列出方程解决问题。
11.1266元
【分析】利息=本金×年利率×时间,据此解答。
【详解】6000×4.22%×5
=253.2×5
=1266(元)
答:到期后她可以捐出1266元。
【点睛】此题考查的目的是理解利息的意义,掌握利息的计算方法及应用。
12.135.02平方米
【分析】求贴瓷砖的面积就是求圆柱的一个底面积和一个侧面积的和,利用S表=πr2+2πrh计算解答。
【详解】3.14×10×1.8+3.14×(10÷2)2
=31.4×1.8+3.14×25
=56.52+78.5
=135.02(平方米)
答:这个水池贴瓷砖的面积是135.02平方米。
【点睛】此题主要考查圆柱体的表面积,解答时一定要注意分清题目中的条件,灵活解答。
13.455.3平方厘米
【分析】由图可知,笔筒是无盖的,求需要多少平方厘米的卡纸,只要求出圆柱的侧面积和一个底面积即可,利用公式,代入数据进行解答即可。
【详解】3.14×10×12+3.14×(10÷2)2
=3.14×120+3.14×25
=376.8+78.5
=455.3(平方厘米)
答:至少需要455.3平方厘米的卡纸。
【点睛】此题主要考查了圆柱体的表面积的意义及在生活中的实际应用。
14.90千米/时
【分析】根据“实际距离=图上距离÷比例尺”求出两城市之间的实际距离,再根据“总路程÷相遇时间=速度和”求出客、货车的速度和,最后用速度和减去货车的速度即可。
【详解】2.7÷=81000000(厘米)
81000000厘米=810千米
810÷5-72
=162-72
=90(千米/时)
答:客车的速度是90千米/时。
【点睛】根据比例尺和图上距离求出实际距离是解答题目的关键。
15.125.6米
【分析】先根据圆锥的体积公式求得圆锥形沙堆的体积;再将路面看作一个长方体,它的体积等于圆锥形沙堆的体积,根据长方体的体积公式可求能铺路面的长度。
【详解】2厘米=0.02米
×31.4×2.4÷(10×0.02)
=×75.36÷0.2
=25.12÷0.2
=125.6(米)
答:能铺125.6米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
16.63元
【分析】把这套运动服的价格看作单位“1”,裤子的价格占这套运动服价格的,根据这套运动服的价格用乘法求出裤子的价格,据此解答。
【详解】144×
=144×
=63(元)
答:裤子的价格是63元。
【点睛】掌握按比例分配问题的解题方法是解答题目的关键。
17.10597.5千克
【分析】根据圆柱的体积公式,先列式计算出粮囤的体积,再将体积乘每立方米玉米的重量750千克,求出这个粮囤能装多少千克玉米。
【详解】3.14×1.52×2×750
=14.13×750
=10597.5(千克)
答:这个粮囤能装10597.5千克玉米。
【点睛】本题考查了圆柱的体积,圆柱的体积=底面积×高。
18.到汇集超市购买较合算,理由见详解
【分析】本题可根据学校要购买水杯的数量及两个商家优惠方案分别进行分析计算即能得出到哪家比较合算。
【详解】九折=90%
4×160×90%
=640×90%
=576(元)
160÷8=20(只)
(160-20)×4
=140×4
=560(元)
576>560
答:到汇集超市购买较合算。
【点睛】解决本题关键是分清楚两个超市不同的优惠方法,找出计算现价的方法,从而得解。
19.120千米
【分析】根据题意,这道题的等量关系是:去时的速度×时间=返回时的速度×时间,根据这个等量关系代入数据,列方程解答。
【详解】解:设原来每小时行x千米。
6x=(x-5)×8
6x=8x-40
6x+40=8x-40+40
6x+40=8x
8x-6x=6x+40-6x
2x=40
2x÷2=40÷2
x=20
20×6=120(千米)
答:甲城到乙城的路程有120千米。
【点睛】本题考查行程问题的解题方法,用方程解答比较简便,解题关键是找出题目中的等量关系,列方程解答。
20.273.6平方米
【分析】龙井柱是圆柱形,刷漆的部分是侧面积,侧面积=底面周长×高,根据公式先求出一个龙井柱的侧面积,再乘4就是四根龙井柱刷漆的总面积,据此解答。
【详解】3×1.2×19×4
=3.6×19×4
=273.6(平方米)
答:刷漆面积共是273.6平方米。
【点睛】此题主要考查了圆柱侧面积的相关应用,注意从题目中提取有效数学信息。
21.10时
【分析】根据实际距离=图上距离÷比例尺,据此求出深圳福田站到北京西站的实际距离,再除以动车的速度即可。
【详解】60÷ =240000000(厘米)
240000000厘米=2400千米
2400÷225=10 (时)
答:G72动车从福田站运行到北京西站大约需要10时。
【点睛】此题主要考查了图上距离和实际距离的换算,换算单位时注意数清0的个数。
22.185厘米
【分析】把“火星1号”高度看作单位“1”,“火星1号”高度×+1=“祝融号”高度,据此解答。
【详解】230×+1
=184+1
=185(厘米)
答:“祝融号”高185厘米。
【点睛】此题主要考查了分数乘法的应用,明确求一个数的几分之几用乘法。
23.(1)300
(2)见详解
【分析】(1)根据已知一个数的百分之几是多少,求这个数,根据扇形统计图和条形统计图提供的信息,150÷50%,就是共调查的人数;
(2)求出D的人数,用总人数-A的人数-B 的人数-C的人数,在补充条形统计图。
【详解】(1)150÷50%=300(人)
(2)300-30-150-90
=270-150-90
=120-90
=30(人)
【点睛】本题考查扇形统计图和条形统计图的应用,根据统计图提供的信息,解答问题。
24.195.936g
【分析】根据圆锥体积公式V=Sh,求出铅锤体积,用体积×每立方厘米重量=铅锤总重量。
【详解】×3.14×2 ×6×7.8
=25.12×7.8
=195.936(克)
答:这个铅锤重195.936g。
【点睛】本题主要考查了圆锥体积,圆锥体积=×底面积×高。
25.(1)复式折线
(2)
(3)30
(4) 陈莉 善于阅读和反思,自制力较强
【分析】(1)图中有两条折线,所以这是一幅复式折线统计图;
(2)李明同学第一次的成绩是80分,第五次练习成绩是92分,比的前项是80,比的后项是92,根据求比值的方法计算;
(3)先求出陈莉第五次的成绩比第一次高多少分,把第一次的成绩看作单位“1”,再根据A比B多百分之几的计算方法:(A-B)÷B×100%求出结果;
(4)通过观察统计图可知,陈莉的成绩提高得更快,主要原因可能是陈莉同学善于阅读和反思,自制力比较强(答案不唯一)。
【详解】(1)这是一幅复式折线统计图。
(2)80∶92
=80÷92
=
所以,李明同学第一次与第五次练习成绩比的比值是。
(3)(91-70)÷70×100%
=21÷70×100%
=0.3×100%
=30%
所以,陈莉同学第五次比第一次练习成绩提高了30%。
(4)由折线统计图可知,陈莉的成绩提高得更快,主要原因可能是陈莉同学善于阅读和反思,自制力较强(答案不唯一)。
【点睛】理解复式折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
26.26次
【分析】根据“圆锥形石子堆的底面周长是25.12米”,先求出石子堆的底面半径,然后求出石子堆的体积,进一步求出石子堆的重量,进而问题得解。
【详解】石子堆的底面半径:25.12÷3.14÷2=4(米)
石子堆的体积:3.14×42×3×=50.24(立方米)
石子的重量:50.24×2=100.48(吨)
要运的次数:100.48÷4≈26(次)
答:要运26次才能运完。
【点睛】先求出石子堆的总重量是解决本题的关键。
27.240页
【分析】把全书总页数看作单位“1”,求全书总页数用没读的64页除以它对应的分率,第一天读了总页数的,第二天读了总页数的的,用1减去两天已读的分率,就是没读页数的分率,据此可解。
【详解】64÷(1--×)
=64÷(-)
=64÷
=240(页)
答:全书共有240页。
【点睛】此题重点考查解决求单位“1”的量的分数问题的方法,解答时用数量除以对应的分率。
28.70块
【详解】解:设如果改用边长6分米的正方形方砖铺地,需要x块.
6×6×x=9×280
36x=2520
x=70
答:如果改用边长6分米的正方形方砖铺地,需要70块。
29.300千克
【分析】把10吨海水可以晒海盐的质量设为未知数,盐的质量÷海水的质量×100%=含盐率(一定),比值一定,海水的千克数和盐的千克数成正比例关系,据此解答。
【详解】10吨=10000千克
解:设10000千克海水可以晒x千克海盐。
15∶500=x∶10000
500x=150000
x=150000÷500
x=300
答:10吨海水可以晒300千克海盐。
【点睛】先判断题中的两种相关联的量成什么比例,并找准对应量是解答题目的关键。
30.1.2小时
【分析】比例尺表示图上距离1cm,实际距离50km。甲、乙两地之间的距离是12厘米,那么实际距离就是12×50=600(km),再根据时间=路程÷速度,计算即可。
【详解】12×50=600(km)
600÷500=1.2(小时)
答:飞到乙地需要1.2小时。
【点睛】此题的关键是先求出甲、乙两地之间的距离,然后再进一步解答。
31.113.04 dm2
【分析】订做的圆柱体铁皮水桶所需的铁皮就是这个圆柱的侧面积加上底面圆的面积,可根据圆柱体的表面积公式:侧面积+底面积;因为这个圆柱体铁通是无盖的,所以只需一个底面积,据此可得出答案。
【详解】底面直径为:(dm),则半径就为2dm,故做这个水桶至少要用铁皮:
=113.04(dm2)
答:做这个水桶至少要用113.04 dm2铁皮。
【点睛】本题主要考查的是圆柱的表面积实际运用,解题时需要注意这个圆柱体铁桶是无盖的,计算时只能计算一个底面圆面积。
32.(1)144元、160元
(2)A商场
【分析】(1)A商场:用标价乘折扣即可求出实际的价格;B商场240元里面有2个100元,可以减去80元,用标价减去优惠掉的80元即为实际的价格;
(2)将两家商场需要的钱数比较即可。
【详解】(1)A商场:六折=60%
240×60%=144(元)
B商场:240÷100=2(个)……40(元)
240-40×2
=240-80
=160(元)
答:在A、B两个商场买各应付144元和160元。
(2)144<160
答:A商场更省钱。
【点睛】理解两家商场的优惠方式是解答本题的关键。
33.80吨
【分析】圆锥的体积=底面积×高×,先计算圆锥的体积,再乘每立方米沙的重量,即可求出这堆沙的总重量。
【详解】3.14×52×1.8××1.7
=3.14×15×1.7
=3.14×25.5
≈80(吨)
答:这堆沙约重80吨。
【点睛】此题考查如何利用圆锥的体积公式进行实际应用,计算结果要用“四舍五入”法。
34.2分球:6个;3分球:2个
【详解】假设投中的全部是2分球,可得:2×8=16(分),比实际得的18分少:18-16=2(分),是因为我们把每个2分球当作了3分球,每个球多算了3-2=1(分),所以可以求出3分球的个数:2÷1=2(个);再进一步解答即可。
【解答】假设投中的全部是2分球:
(18-2×8)÷(3-2)
=2÷1
=2(个)
8-2=6(个)
答:他投进2分球6个,3分球2个。
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法进行分析比较,进而得出结论;也可以用方程,设其中的一个数为未知数,另一个数也用未知数表示,列出方程解答即可。
35.180÷(-35%)=1200(kg)
【详解】略
36.48页
【分析】根据乘数的意义,第一天看的页数=全书的页数×;第二天看的页数=余下的页数×;余下的页数=全书页数-第一天看的页数;第一天的页数+第二天的页数=两天一共看的页数。
【详解】120×+(120-120×)×
=24+(120-24)×
=24+96×
=24+24
=48(页)
答:两天一共看了48页。
【点睛】分析题目数量之间的关系,根据数量之间的关系列出数量关系式,根据数量关系式解决问题。
37.10%
【分析】通常把“比”后的量看作单位“1”,把第一季度的营业额看作单位“1”。用两季度营业额之差除以第一季度的营业额,即可求出第二季度的营业额比第一季度增长了百分之几。
【详解】(16.5-15)÷15
=1.5÷15
=10%
答:第二季度的营业额比第一季度增长了10%。
【点睛】求一个数比另一个数多/少百分之几,用两数之差除以另一个数。
38.(1)见详解;
(2)16
【分析】(1)将三角形按2∶1的比放大,则放大后的边长为原来边长的2倍,据此画出放大后的图形即可;
(2)根据“s=ah÷2”求出放大后的图形的面积即可。
【详解】(1)如图:
(2)8×4÷2=16(平方厘米)
【点睛】熟练掌握图形放大与缩小的方法是解答本题的关键。
39.14.5米
【分析】同一时间,同一地点测得物体与影子的比值相等,它们成正比例关系,也就是米尺的长度与影子的比等于树的高与影子的比,设这棵老树的高为x米,组成比例,解比例即可。
【详解】解:设这棵老树的高为x米。
x∶8.7=1∶0.6
0.6x=8.7×1
0.6x=8.7
x=14.5
答:这棵老树的高度是14.5米。
【点睛】解答此题的关键是,判断实际高度与影子成正比例,由此列出比例解决问题。
40.(1)100.48平方分米;
(2)35升
【分析】(1)将数据代入到圆柱的表面积公式:S=中计算即可。
(2)将数据代入到圆柱的容积公式:V=中计算即可。
【详解】(1)3.14×(4÷2)2×2+3.14×4×6
=3.14×22×2+12.56×6
=3.14×4×2+75.36
=25.12+75.36
=100.48(平方分米)
答:外壳的表面积是100.48平方分米。
(2)3.14×(3÷2)2×5
=3.14×1.52×5
=3.14×2.25×5
=3.14×11.25
≈35(立方分米)
35立方分米=35升
答:内胆的容积约是35升。
【点睛】本题主要考查圆柱的表面积、容积公式的实际应用。
41.(1)80人;(2)图见详解;(3)25%
【分析】(1)总人数=美术人数÷美术人数所占百分率;
(2)足球人数=总人数×足球人数所占百分率,据此补全条形统计图;
(3)用演讲人数与足球人数之差除以演讲人数即可。
【详解】(1)10÷12.5%=80(人)
答:抽样调查总人数有80人。
(2)80×18.75%=15(人)
作图如下:
(3)(20-15)÷20
=5÷20
=25%
答:“足球”的人数比“演讲”的人数少25%。
【点睛】此题考查条形统计图和扇形统计图的综合应用,能够从统计图中提取有效数学信息是解题关键。
42.(1);
上午8:00到上午11:00行驶了3小时,行驶了300千米,图上距离是6厘米
(2)不需要
(3)12点40分
【分析】(1)上午8:00到上午11:00行驶了3小时,小车的速度×行驶的时间求出行驶的路程,根据实际距离×比例尺=图上距离,求出上午11:00时小车行驶的图上距离,据此作图;
(2)根据图上距离÷比例尺=实际距离求出甲地到乙地的实际距离,再除以100千米求出有多少个100,再乘以8升求出消耗的汽油,最后再与出发时油箱里的油比较;
(3)原来小车的速度×(1-10%)求出现在小车的速度,甲地到乙地的距离-上午11:00前行驶的路程求出剩下的路程,再除以现在小车的平均速度求出还需要行驶的时间,上午11:00加上还需要行驶的时间即为李老师到达乙地的最早时间。
【详解】(1)11:00-8:00=3(小时)
100×3=300(千米)=30000000(厘米)
30000000×=6(厘米)
作图如下:
(2)9÷=45000000(厘米)=450(千米)
450÷100×8
=4.5×8
=36(升)
36升<40升
答:中途不需要再加油。
(3)100×(1-10%)
=100×90%
=90(千米)
(450-300)÷90
=150÷90
=1(小时)
1=1小时40分
11:00+1小时40分=12:40
答:李老师到达乙地的最早时间是12点40分。
【点睛】掌握图上距离、实际距离、比例尺之间的关系是解答此题的关键。
43.11.775立方厘米
【分析】看图可知,圆锥底面直径是3厘米,高是5厘米,根据圆锥体积=底面积×高÷3,列式解答即可。
【详解】3.14×(3÷2) ×5÷3
=3.14×2.25×5÷3
=11.775(立方厘米)
答:这个零件的体积是11.775立方厘米。
【点睛】关键是通过观察确定圆锥的底面直径和高。
44.(1)20平方分米
(2)0.6立方分米
【分析】(1)正方体玻璃容器(无盖),则玻璃的面积应是5个面的面积;
(2)土豆的体积等于水面上升部分的体积,用水与土豆的体积之和减去水的体积得到土豆的体积。
【详解】(1)2×2×5
=4×5
=20(平方分米)
答:这个玻璃容器至少需要20平方分米的玻璃。
(2)5升=5立方分米
14厘米=1.4分米
2×2×1.4-5
=5.6-5
=0.6(立方分米)
答:土豆的体积是0.6立方分米。
【点睛】本题考查正方体的表面积、求不规则物体的体积,解答本题的关键是掌握求不规则物体的体积的方法。
45.见详解
【分析】(1)求出图1总人数,总人数-乘车感染数-旅游感染数-舍去感染数=聚餐感染数,据此将图2补充完整;
(2)答案不唯一,如2月2日和2月3日两天的感染人数是1月31日感染人数的几倍,求出2月2日和2月3日两天的感染人数和,除以1月31日感染人数即可;
(3)答案不唯一,合理即可。
【详解】(1)5+9+5+6+4+6-8-9-2
=35-19
=16(人)
(2)问题:2月2日和2月3日两天的感染人数是1月31日感染人数的几倍?
列式:(6+4)÷5
(3)减少聚餐,因为聚餐导致的感染人数非常多。
【点睛】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较。
46.(1)56%
(2)499百万件
【分析】(1)用申通快递的业务量除以韵达快递业务量,再乘100%,其结果百分号前保留整数即可;
(2)根据已知比一个数多百分之几的数是多少,求这个数,用除法解答即可。
【详解】(1)390÷701×100%
≈0.56×100%
=56%
答:2021年2月,申通快递的业务量是韵达快递业务量的56%。
(2)699÷(1+40%)
=699÷1.4
≈499(百万件)
答:顺丰快递2020年2月的快递业务量约是499百万件。
【点睛】本题考查求一个数占另一个数的百分之几,明确用除法是解题的关键。
47.2.25小时
【分析】根据路程一定,速度与时间成反比例,由此列出比例解答即可。
【详解】解:设x小时可回到出发地。
3.2x=3.6×2
3.2x=7.2
3.2x÷3.2=7.2÷3.2
x=2.25
答:2.25小时可回到出发地。
【点睛】解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;再列出比例解答即可。
48.(1)44平方分米;(2)18.84升
【分析】(1)一个水桶需要的铁皮的面积=水桶的侧面积+底面积,利用圆柱的侧面积和圆的面积公式即可得解,得数再乘2即可;
(2)先根据圆柱的容积V=πr2h,求出一个水桶的容积,再乘2就是一对水桶的容积。
【详解】(1)3.14×20×30+3.14×(20÷2)2
=1884+314
=2198(平方厘米)
2198×2=4396(平方厘米)
4396平方厘米≈44平方分米
答:做这样一对水桶大约需要44平方分米铁皮。
(2)3.14×(20÷2)2×30
=3.14×100×30
=9420(立方厘米)
9420立方厘米=9.42升
9.42×2=18.84(升)
答:这对水桶可以装水18.84升。
【点睛】此题主要考查圆柱的表面积和圆柱的体积的计算方法,要记住求的是一对水桶需要的铁皮的面积和容积。
49.5公顷
【分析】根据题意,把果园的总面积看作单位“1”,已知种桃树和李子树的总面积与种樱桃树的面积的比是7∶5,那么种桃树和李子树的总面积就占果园总面积的,种樱桃树的面积就占果园总面积的,种李子树的面积就占果园总面积的(-),它对应的面积是2.5公顷,据此用除法计算求出果园总面积,再乘种樱桃树的面积所占的分率即可求出种樱桃树的面积是多少公顷。
【详解】2.5÷(-)×
=2.5÷×
=5(公顷)
答:种樱桃树的面积是5公顷。
【点睛】本题主要考查比的实际应用,解答本题的关键是求出三种果树种植面积各自占果园总面积的分率。
50.乙商场
【分析】分析题意,甲商场购物满300元返现金40元,将皮鞋的价钱与40元相减,计算得出淘气妈妈在甲商场实际付出的钱数;乙商场所有商品一律八五折出售,将皮鞋的价钱与85%相乘,计算得出淘气妈妈在乙商场实际付出的钱数,不难解答本题。
【详解】400-40=360(元)
400×85%=340(元)
340<360
答:淘气妈妈到乙商场购买更优惠。
【点睛】本题是一道折扣问题,需结合折扣问题中的数量关系,求一个数的百分之几的知识进行求解。
51.30立方米
【分析】先利用圆锥的体积V=Sh,求出这些谷子的体积,进而利用已知一个数的几百分之几是多少,求这个数,用除法计算的方法,即可求出这个粮仓的容积。
【详解】18分米=1.8米
×10×1.8÷20%
=6÷20%
=30(立方米)
答:这个粮仓的容积是30立方米。
【点睛】此题主要考查圆锥的体积的计算方法在实际中的应用。
52.20千克
【分析】先把甲袋大米的质量看作单位“1”,取出后,再剩下(1-),根据分数乘法的意义,即可求出此时甲袋所剩大米的质量。再把甲袋所剩大米的质量平均分成8份,先用除法求出1份的质量,再用乘法求出3份的质量,即乙袋取出25%后剩大米的质量。再把乙袋原来大米的质量看作单位“1”,根据百分数除法的意义,用乙袋所剩大米的质量除以(1-25%),就是乙袋大米原来的质量。
【详解】60×(1-)÷8×3÷(1-25%)
=60×÷8×3÷75%
=20(千克)
答:乙袋中原来有20千克大米。
【点睛】关键是根据分数乘法的意义,求出甲袋取出后剩下的质量。除按上述解答方法外,也可把比转化成分数,求出乙袋取出25%后剩的质量,然后再根据百分数除法的意义,求乙袋原来的质量。
53.(1)32立方米(2)30立方米
【分析】(1)用乐乐家六月末水表读数减去五月末水表读数就是乐乐家六月份的用水量。
(2)根据阶梯收费的方法逐步求出a的值。
【详解】(1)143-111=32(立方米)
答:六月份共用了32立方米水。
(2)将32立方米水的收费进行分级:
第一级:用水量20立方米,用水费:20×1.74=34.8(元)
剩余的12立方米水,共交水费:68.58-34.8=33.78(元)
(33.78-2.61×12)÷(3.84-2.61)
=2.46÷1.23
=2(立方米)
12-2=10(立方米)
按第三级收费的有2立方米,则按第二级收费的10立方米。
20+10=30(立方米)
答:当用水30立方米以上时收费标准是3.84元/立方米。
【点睛】本题考查了阶梯收费问题,难度较大,需认真分析题目中的数量关系。
54.(1)490千米
(2)小时
【详解】(1)196÷(80%+-1)
=196÷
=490(千米)
答:全程是490千米。
(2)客车与货车的速度比是: ∶80%=3∶4
相遇时货车行的路程为:490×=280(千米)
货车的速度为:280÷5=56(千米/小时)
490÷56=(小时)
答:货车行完全程需要小时。
55.够
【分析】根据利息=本金×时间×利率,求出到期时小芳的利息,因为银行的利息税是5%,所以实得利息为所得利息的(1-5%),根据乘法的意义,求出实得利息。书包的售价=原价×85%,与实得利息比较即可。
【详解】500×2×4.50%×(1-5%)
=45×95%
=42.75(元);
50×85%=42.5(元)
42.75>42.5
答:钱够。
【点睛】此题考查属于百分数的综合性题目,关键是求出实得利息与书包的售价。明确求一个数的百分之几是多少用乘法。
56.100个
【分析】根据题意,把当天桃子总数看作单位“1”,则第9天摘之前树上的桃子数是10÷(1-),同理,第8天摘之前树上的桃子是第9天桃子总数(第8天剩下的桃子数)的(1-),依此类推,用除法求出桃子总数即可。
【详解】10÷(1-)÷(1-)÷…÷(1-)
=10÷÷…
=10×2××…×
=10×10
=100(个)
答:树上原来有100个桃子。
【点睛】本题主要考查逆推问题,关键求摘之前树上桃子的数量。
57.甲车间原来有60人,乙车间原来有96人
【分析】把乙车间原来的人数看作单位“1”,由题意可知,乙车间比甲车间多2个18人,即(18×2)人,这(18×2)人正好是乙车间人数的(1-),根据分数除法的意义,用(18×2)人除以(1-),就是乙车间原来的人数。再根据分数乘法的意义,用乙车间原来的人数乘,就是甲车间原来的人数。
【详解】18×2÷(1-)
=36÷
=96(人)
96×=60(人)
答:甲车间原来有60人,乙车间原来有96人。
【点睛】此题是考查分数乘、除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
答案第4页,共25页
答案第3页,共25页
同课章节目录
