苏科版八年级上册第1章全等三角形(探究全等三角形中常见模型)(无答案)
文档属性
| 名称 | 苏科版八年级上册第1章全等三角形(探究全等三角形中常见模型)(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 549.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 10:37:22 | ||
图片预览



文档简介
第1章全等三角形(探究全等三角形中常见模型)
【学习目标】
1.掌握“一线三等角”模型的做题方法;
2.掌握“半角”模型的做题方法;
3.掌握“手拉手”模型的做题方法.
【典型例题】
类型一、 “一线三等角”模型
1.(1)如图1,直线m经过等边三角形ABC的顶点A,在直线m上取两点D,E,使得∠ADB=60°,∠AEC=60°.求证:BD+CE=DE;
(2)将(1)中的直线m绕着点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.若BD=3,CE=7,求DE的长.
举一反三:
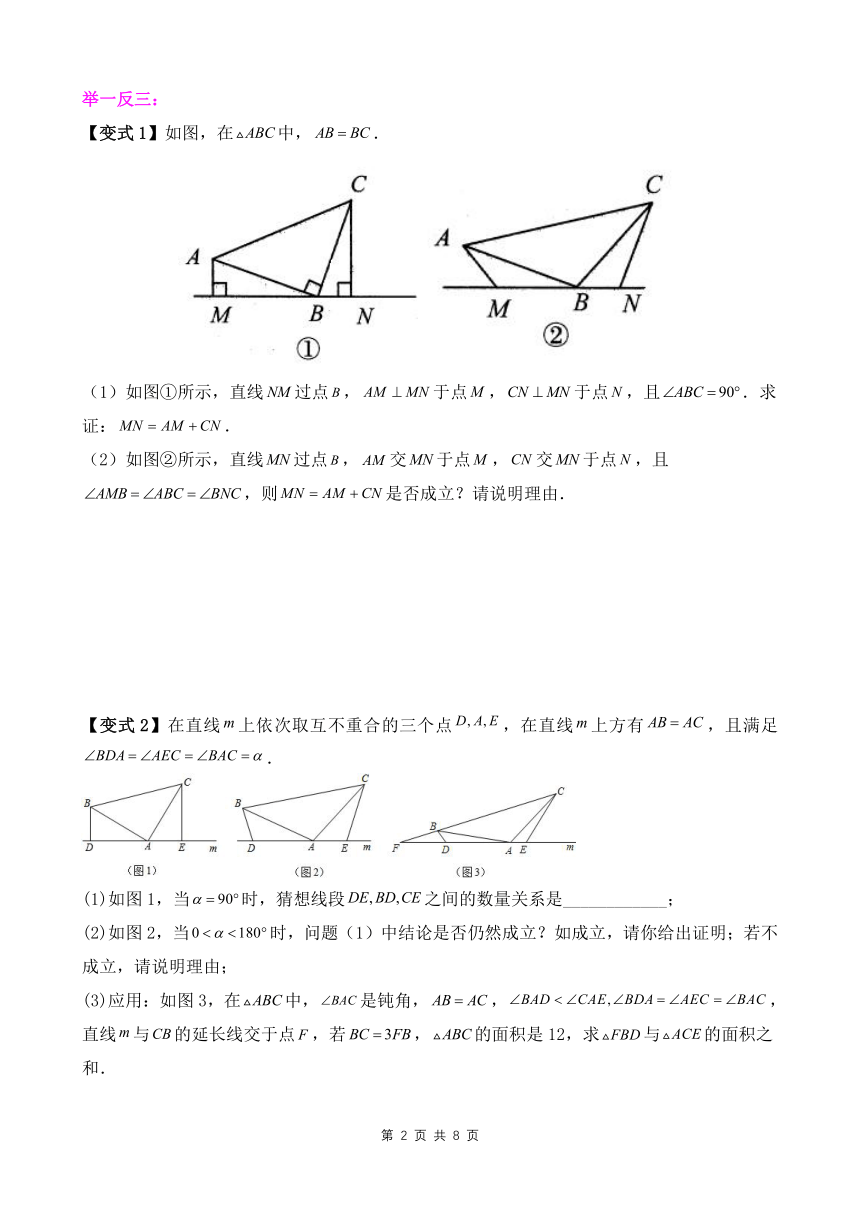
【变式1】如图,在中,.
(1)如图①所示,直线过点,于点,于点,且.求证:.
(2)如图②所示,直线过点,交于点,交于点,且,则是否成立?请说明理由.
【变式2】在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;
(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
【变式3】已知:是经过的顶点C的一条直线,.E、F是直线上两点,.
(1)若直线经过的内部,.
①如图1,,,直接写出,,间的等量关系:__________.
②如图2,与具有怎样的数量关系,能使①中的结论仍然成立?写出与的数量关系,并对结论进行证明;
(2)如图3,若直线经过的外部,,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
【变式4】在△ABC中,∠ACB= 900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,△ADC≌△CEB,且 DE=AD+BE。你能说出其中的道理吗?
(2)当直线MN绕点C旋转到图2的位置时, DE =AD-BE。说说你的理由。
(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE 具有怎样的等量关系?请写出这个等量关系。
类型二、 “半角”模型
2.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于点G,以下五个结论:①∠B=∠C=45°;②AP=EF;③∠AFP和∠AEP互补;④△EPF是等腰直角三角形;⑤四边形AEPF的面积是△ABC面积的,其中正确结论是( )
A.①②③ B.①②④⑤ C.①③④⑤ D.①③④
举一反三:
【变式1】如图,已知正方形ABCD的边长为3,点E,F分别是AB,BC边上的点,且∠EDF=45°,将△ADE绕点D逆时针旋转90°得到△CDM.若AE=1,则MF的长为 .
【变式2】已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm.
(1)如图①,O是正方形ABCD对角线的交点,若OM⊥ON,求四边形MONC的面积;
(2)如图②,若∠MAN=45°,求△MCN的周长.
【变式3】问题情境
在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.
特例探究:如图1,当DM=DN时,
(1)∠MDB= 度;
(2)MN与BM,NC之间的数量关系为 ;
归纳证明:
(3)如图2,当DM≠DN时,在NC的延长线上取点E,使CE=BM,连接DE,猜想MN与BM,NC之间的数量关系,并加以证明.
拓展应用:
(4)△AMN的周长与△ABC的周长的比为 .
【变式4】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)
类型三、 “手拉手”模型
3.如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F.
(1)求证:AE=DC;
(2)求∠BFE的度数;
(3)若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.
举一反三:
【变式1】已知:两个等腰直角三角板△ACB和△DCE(AC=BC,DC=CE,∠ACB=∠DCE=90°)如图所示摆放,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1(两个等腰直角三角板大小不等),试判断AE与BD有何关系并说明理由;
(2)如图2(两个等腰直角三角板大小相等,即AC=DC),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.
【变式2】已知:等腰和等腰中,,,.
(1)如图1,延长交于点,若,则的度数为 ;
(2)如图2,连接、,延长交于点,若,求证:点为中点;
(3)如图3,连接、,点是的中点,连接,交于点,,,直接写出的面积.
【变式3】(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
【变式4】如图,△CAB与△CDE为等腰直角三角形,∠ACB=∠DCE=90°,CA=CB,CD=CE,∠CAB=∠CBA=45°,∠CDE=∠CED=45°,连接AD、BE.
(1)如图1,若∠CAD=28°,∠DCB=10°,则∠DEB的度数为 度;
(2)如图2,若A、D、E三点共线,AE与BC交于点F,且CF=BF,AD=3,求△CEF的面积;
(3)如图3,BE与AC的延长线交于点G,若CD⊥AD,延长CD与AB交于点N,在BC上有一点M且BM=CG,连接NM,请猜想CN、NM、BG之间的数量关系并证明你的猜想.
【学习目标】
1.掌握“一线三等角”模型的做题方法;
2.掌握“半角”模型的做题方法;
3.掌握“手拉手”模型的做题方法.
【典型例题】
类型一、 “一线三等角”模型
1.(1)如图1,直线m经过等边三角形ABC的顶点A,在直线m上取两点D,E,使得∠ADB=60°,∠AEC=60°.求证:BD+CE=DE;
(2)将(1)中的直线m绕着点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.若BD=3,CE=7,求DE的长.
举一反三:
【变式1】如图,在中,.
(1)如图①所示,直线过点,于点,于点,且.求证:.
(2)如图②所示,直线过点,交于点,交于点,且,则是否成立?请说明理由.
【变式2】在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;
(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
【变式3】已知:是经过的顶点C的一条直线,.E、F是直线上两点,.
(1)若直线经过的内部,.
①如图1,,,直接写出,,间的等量关系:__________.
②如图2,与具有怎样的数量关系,能使①中的结论仍然成立?写出与的数量关系,并对结论进行证明;
(2)如图3,若直线经过的外部,,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
【变式4】在△ABC中,∠ACB= 900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,△ADC≌△CEB,且 DE=AD+BE。你能说出其中的道理吗?
(2)当直线MN绕点C旋转到图2的位置时, DE =AD-BE。说说你的理由。
(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE 具有怎样的等量关系?请写出这个等量关系。
类型二、 “半角”模型
2.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于点G,以下五个结论:①∠B=∠C=45°;②AP=EF;③∠AFP和∠AEP互补;④△EPF是等腰直角三角形;⑤四边形AEPF的面积是△ABC面积的,其中正确结论是( )
A.①②③ B.①②④⑤ C.①③④⑤ D.①③④
举一反三:
【变式1】如图,已知正方形ABCD的边长为3,点E,F分别是AB,BC边上的点,且∠EDF=45°,将△ADE绕点D逆时针旋转90°得到△CDM.若AE=1,则MF的长为 .
【变式2】已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm.
(1)如图①,O是正方形ABCD对角线的交点,若OM⊥ON,求四边形MONC的面积;
(2)如图②,若∠MAN=45°,求△MCN的周长.
【变式3】问题情境
在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.
特例探究:如图1,当DM=DN时,
(1)∠MDB= 度;
(2)MN与BM,NC之间的数量关系为 ;
归纳证明:
(3)如图2,当DM≠DN时,在NC的延长线上取点E,使CE=BM,连接DE,猜想MN与BM,NC之间的数量关系,并加以证明.
拓展应用:
(4)△AMN的周长与△ABC的周长的比为 .
【变式4】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)
类型三、 “手拉手”模型
3.如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F.
(1)求证:AE=DC;
(2)求∠BFE的度数;
(3)若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.
举一反三:
【变式1】已知:两个等腰直角三角板△ACB和△DCE(AC=BC,DC=CE,∠ACB=∠DCE=90°)如图所示摆放,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1(两个等腰直角三角板大小不等),试判断AE与BD有何关系并说明理由;
(2)如图2(两个等腰直角三角板大小相等,即AC=DC),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.
【变式2】已知:等腰和等腰中,,,.
(1)如图1,延长交于点,若,则的度数为 ;
(2)如图2,连接、,延长交于点,若,求证:点为中点;
(3)如图3,连接、,点是的中点,连接,交于点,,,直接写出的面积.
【变式3】(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
【变式4】如图,△CAB与△CDE为等腰直角三角形,∠ACB=∠DCE=90°,CA=CB,CD=CE,∠CAB=∠CBA=45°,∠CDE=∠CED=45°,连接AD、BE.
(1)如图1,若∠CAD=28°,∠DCB=10°,则∠DEB的度数为 度;
(2)如图2,若A、D、E三点共线,AE与BC交于点F,且CF=BF,AD=3,求△CEF的面积;
(3)如图3,BE与AC的延长线交于点G,若CD⊥AD,延长CD与AB交于点N,在BC上有一点M且BM=CG,连接NM,请猜想CN、NM、BG之间的数量关系并证明你的猜想.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
