25.3.1解直角三角形(广东省佛山市顺德区)
文档属性
| 名称 | 25.3.1解直角三角形(广东省佛山市顺德区) |  | |
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-24 14:26:00 | ||
图片预览




文档简介
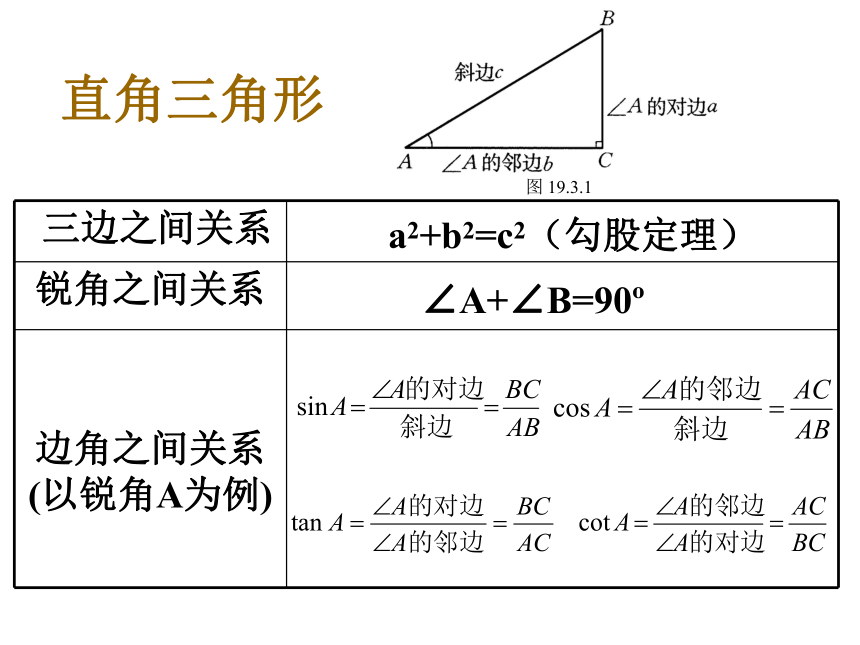
课件12张PPT。25.3.1解直角三角形直角三角形a2+b2=c2(勾股定理)∠A+∠B=90o练习:
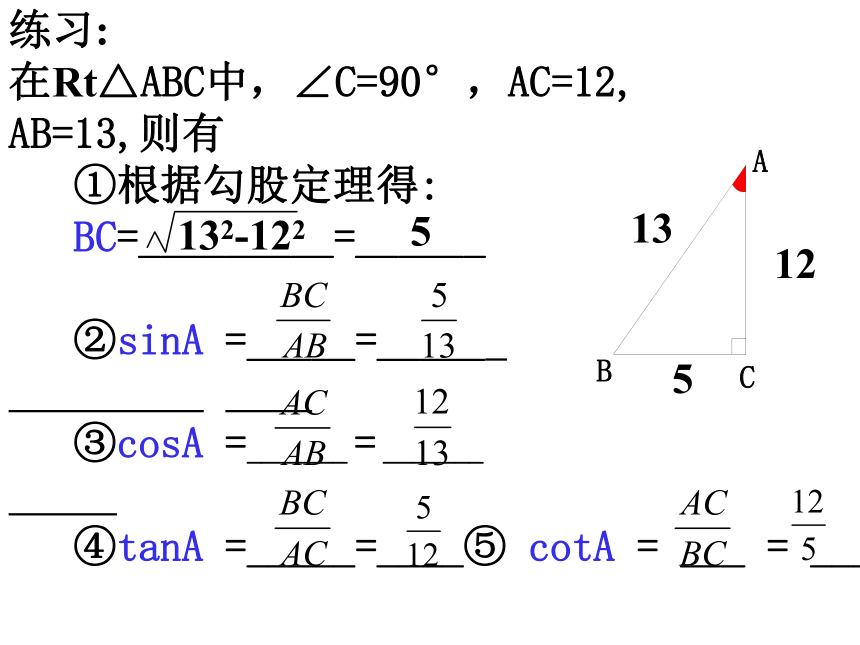
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___5132-12212135练习1:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方? 1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形 ;3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。2、在解决实际问题时,应“先画图,再求解”; 概括4、在直角三角形中,如果已知两条边的长
度,能否求出另外两个锐角?虎门威远炮台 虎门威远的东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求:
(1)敌舰C与炮台A的距离;
(2)敌舰C与炮台B的距离.
(精确到1米) (1)在直角三角形中,已知一条边
和一个锐角,可利用三角函数来求另外
的边 .注意: (2)解直角三角形过程中,常会遇
到近似计算,本书除特别说明外,边长
保留四个有效数字,角度精确到
练习2:海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求
(1)从A处到B处的距离;
(2)灯塔Q到B处的距离
(画出图形后计算,
精确到 0.1 海里) 小结
①定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;②在解决实际问题时,应“先画图,再求解”;
③解直角三角形,只有下面两种情况可解:
(1)已知两条边;
(2)已知一条边和一个锐角。
在Rt△ABC中,∠C=90°,AC=12,
AB=13,则有
①根据勾股定理得:
BC=_________=______
②sinA =_____=_____
③cosA =_______ = _______
④tanA =_____=____⑤ cotA = ___ = ___5132-12212135练习1:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方? 1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形 ;3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。2、在解决实际问题时,应“先画图,再求解”; 概括4、在直角三角形中,如果已知两条边的长
度,能否求出另外两个锐角?虎门威远炮台 虎门威远的东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求:
(1)敌舰C与炮台A的距离;
(2)敌舰C与炮台B的距离.
(精确到1米) (1)在直角三角形中,已知一条边
和一个锐角,可利用三角函数来求另外
的边 .注意: (2)解直角三角形过程中,常会遇
到近似计算,本书除特别说明外,边长
保留四个有效数字,角度精确到
练习2:海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求
(1)从A处到B处的距离;
(2)灯塔Q到B处的距离
(画出图形后计算,
精确到 0.1 海里) 小结
①定义:在直角三角形中,由已 知元素求出未知元素的过程,叫做解直角三角形;②在解决实际问题时,应“先画图,再求解”;
③解直角三角形,只有下面两种情况可解:
(1)已知两条边;
(2)已知一条边和一个锐角。
