人教版九年级数学下册 《27.2.3相似三角形的应用举例第2课时》教学课件(共22张PPT)
文档属性
| 名称 | 人教版九年级数学下册 《27.2.3相似三角形的应用举例第2课时》教学课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 490.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
相似三角形的应用举例
学习目标
能够利用相似三角形的对应边成比例来解决河流宽度的问题;
掌握构建相似三角形的常见方法,灵活设计解决方案解决问题.
进一步体会数学的应用价值,提升学生的应用意识;
4. 探究经历构造相似三角形的方法与技巧,体会把实际问题转化为数学问题来解决的过程,增加学习兴趣,培养学生发现问题、解决问题的能力.
重点
测量河宽
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
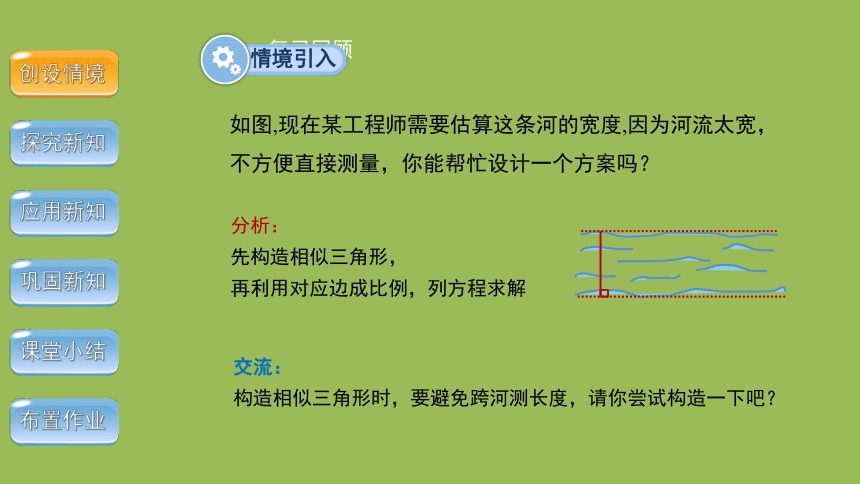
如图,现在某工程师需要估算这条河的宽度,因为河流太宽,不方便直接测量,你能帮忙设计一个方案吗?
分析:
先构造相似三角形,
再利用对应边成比例,列方程求解
交流:
构造相似三角形时,要避免跨河测长度,请你尝试构造一下吧?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)在河对岸选定一个目标点P ,
(2)在近岸取点 Q 和 S ,使点 P、Q、S三点共线,且直线 PS 与河垂直,则PQ的长就是河的宽度
b
Q
S
P
问题:你能构造出怎样的相似三角形,来计算河宽PQ的长呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
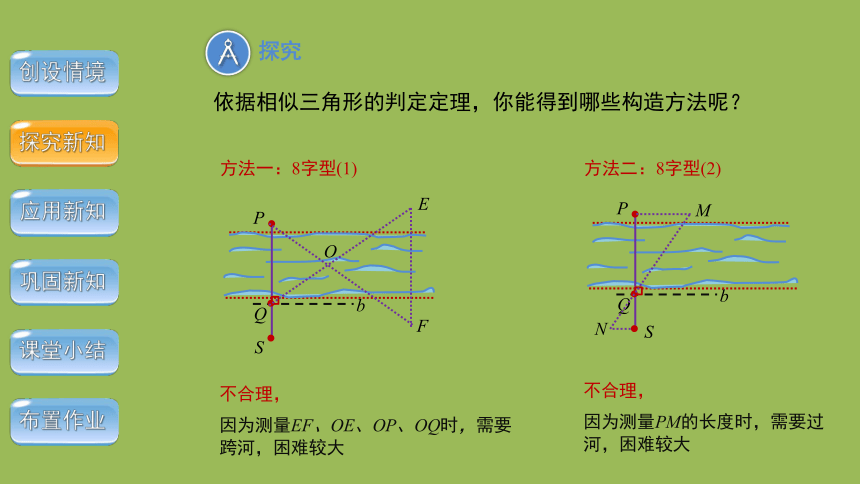
依据相似三角形的判定定理,你能得到哪些构造方法呢?
P
Q
S
b
不合理,
因为测量EF、OE、OP、OQ时,需要跨河,困难较大
方法一:8字型(1)
P
Q
S
b
M
N
方法二:8字型(2)
不合理,
因为测量PM的长度时,需要过河,困难较大
E
F
O
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
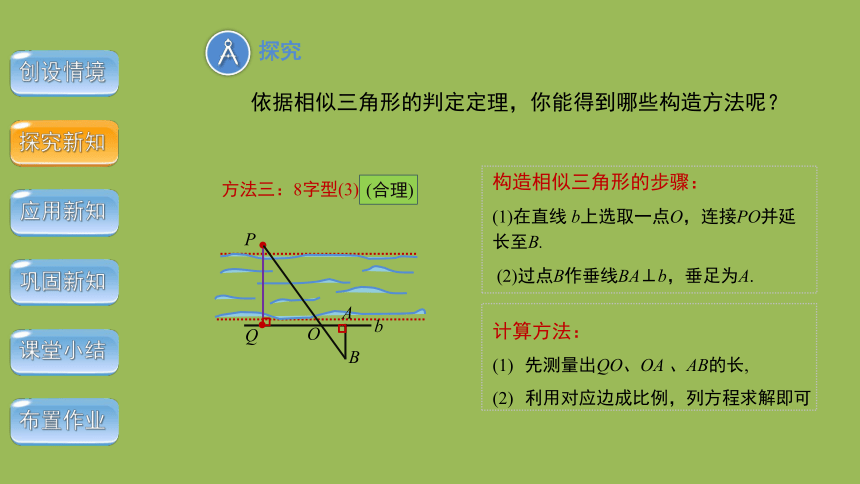
依据相似三角形的判定定理,你能得到哪些构造方法呢?
(合理)
方法三:8字型(3)
P
Q
O
b
B
A
构造相似三角形的步骤:
(1)在直线 b上选取一点O,连接PO并延长至B.
(2)过点B作垂线BA⊥b,垂足为A.
计算方法:
先测量出QO、OA 、AB的长,
利用对应边成比例,列方程求解即可
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
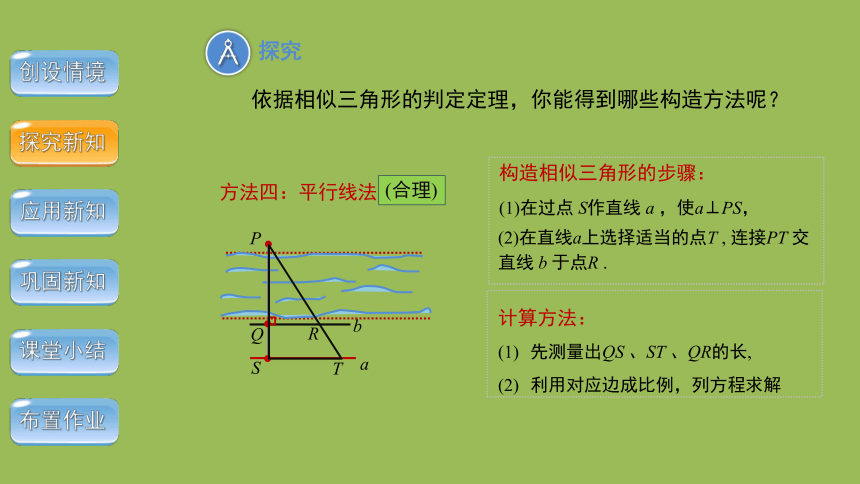
依据相似三角形的判定定理,你能得到哪些构造方法呢?
P
b
(合理)
方法四:平行线法
Q
S
a
T
R
构造相似三角形的步骤:
(1)在过点 S作直线 a ,使a⊥PS,
计算方法:
先测量出QS 、ST 、QR的长,
利用对应边成比例,列方程求解
(2)在直线a上选择适当的点T , 连接PT 交 直线 b 于点R .
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
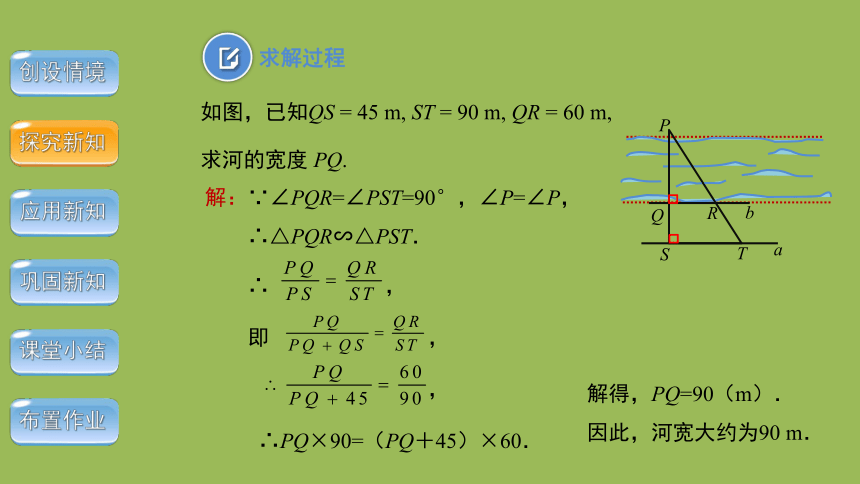
求解过程
如图,已知QS = 45 m, ST = 90 m, QR = 60 m,
求河的宽度 PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST.
∴ ,
即 ,
,
∴PQ×90=(PQ+45)×60.
P
Q
R
S
T
a
b
解得,PQ=90(m).
因此,河宽大约为90 m.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
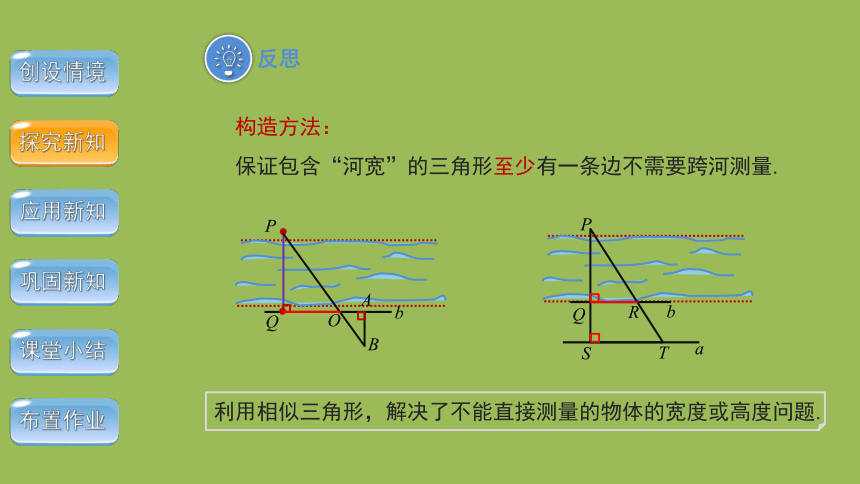
反思
P
Q
R
S
T
a
b
利用相似三角形,解决了不能直接测量的物体的宽度或高度问题.
P
Q
O
b
B
A
构造方法:
保证包含“河宽”的三角形至少有一条边不需要跨河测量.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
反思
思考:如何测量池塘的宽度PQ呢?
P
Q
O
E
F
P
Q
O
E
F
你还有其他方法吗?
全等三角形法
中位线法
“全等三角形法” 与“中位线法” 是“相似三角形法”的特殊情形.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
利用相似三角形可以解决下面的2个问题
总结
测高:不易到达顶部,不能直接使用测量工具;
测距:不易直接测量的两点间的距离.
阅读问题
体会情境
抽象模型
构造相似
总结归纳
回归实际
画出图形
解决问题
一般步骤
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1.如图,左、右并排的两棵树的高分别是AB=8 m和CD=12 m,两树相距BD=5 m,一个人估计自己眼睛距地面的距离是EF=1.6 m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?
A
B
C
D
E
F
l
A
B
C
D
E
F
l
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
分析:如图1,设眼睛的位置为点F,
水平视线FG分别交AB,CD于点H,K.
∠AFH是观察点A时的仰角.
B
D
E
A
C
H
K
G
F
l
Ⅰ
Ⅱ
由于树的遮挡,区域Ⅰ是盲区.
同样地,∠CFK是观察点C时的仰角,
区域Ⅱ是盲区
图1
如图2,当某人从左向右移动过程中,
(1)当走到O点时,点F、A、C三点刚好共线
(临界位置),
O
(2)在点O的右边时,无法看到点C.
(3)在点O的左边时,可以看到点C.
图2
最近距离是BO
盲区
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解:如图,假设观察者从左向右走到点O时,她的眼睛的位置点F与两棵树的顶端点A,C恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AFH∽△CFK.
∴ ,
A
B
C
D
E
F
l
O
最近距离是BO
H
K
G
∵AB=8 m、CD=12 m,
BD=5 m,OF=1.6 m
解得 FH=8(m).
由此可知,当她与左边的树的距离小于8 m时,她看不到右边树的顶端C.
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
数学建模思想:
把生活中的实际问题通过建模的思想,转化为数学问题来解决
一般步骤:
(1)根据题设中的已知量与未知量画出数学示意图,
(2)抽象出几何位置关系
(3)根据几何图形的知识解决实际问题.
A
B
C
D
F
l
O
H
K
G
该例题的关键是找到临界位置,满足F、A、C三点共线
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1. 如图,小明在 A 时测得某树的影长为 2 m,B 时又测得该树的影长为 8 m,若两次日照的光线互相垂直,则树的高度为____m.
A时
B时
A
B
C
D
解:设树的高度是x米,因为
4
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.小王同学,测树时发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7m,留在墙上部分的影长为1m,同时,小明测得长为1m的竹竿影长为0.9m.请计算这棵树的高.
1
分析:
利用相似三角形的知识解决.先构造出相似三角形,再列方程求解
1m
0.9m
由于太阳光线是平行线,所以,可以构成右图所示的相似三角形.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1
因此这棵树的高为4米.
解:过点D作 交AB于点F.
1m
0.9m
P
Q
R
A
B
C
D
F
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
思考:关于这道题你还有其他构造相似三角形的方法吗?
1m
0.9m
P
Q
R
方法一
A
B
C
D
F
1m
0.9m
P
Q
R
方法二
A
B
C
D
E
1
2.7
x
1m
0.9m
P
Q
R
方法三
A
B
C
D
F
2.7
x-1
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
测高与测距问题的解决方法:
测量河流的宽度的方法
构造相似三角形注意事项:
保证包含“河宽”的三角形至少有一条边不需要跨河测量.
利用相似三角形测量河宽
构造相似三角形:(1)8字型相似三角形;(2)平行线法相似三角形
P
Q
O
b
B
A
P
Q
R
S
T
a
b
通过构造相似三角形进行解决,根据不同的实际情况
选择合适的方法
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
相似三角形的应用举例
学习目标
能够利用相似三角形的对应边成比例来解决河流宽度的问题;
掌握构建相似三角形的常见方法,灵活设计解决方案解决问题.
进一步体会数学的应用价值,提升学生的应用意识;
4. 探究经历构造相似三角形的方法与技巧,体会把实际问题转化为数学问题来解决的过程,增加学习兴趣,培养学生发现问题、解决问题的能力.
重点
测量河宽
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
如图,现在某工程师需要估算这条河的宽度,因为河流太宽,不方便直接测量,你能帮忙设计一个方案吗?
分析:
先构造相似三角形,
再利用对应边成比例,列方程求解
交流:
构造相似三角形时,要避免跨河测长度,请你尝试构造一下吧?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)在河对岸选定一个目标点P ,
(2)在近岸取点 Q 和 S ,使点 P、Q、S三点共线,且直线 PS 与河垂直,则PQ的长就是河的宽度
b
Q
S
P
问题:你能构造出怎样的相似三角形,来计算河宽PQ的长呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
依据相似三角形的判定定理,你能得到哪些构造方法呢?
P
Q
S
b
不合理,
因为测量EF、OE、OP、OQ时,需要跨河,困难较大
方法一:8字型(1)
P
Q
S
b
M
N
方法二:8字型(2)
不合理,
因为测量PM的长度时,需要过河,困难较大
E
F
O
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
依据相似三角形的判定定理,你能得到哪些构造方法呢?
(合理)
方法三:8字型(3)
P
Q
O
b
B
A
构造相似三角形的步骤:
(1)在直线 b上选取一点O,连接PO并延长至B.
(2)过点B作垂线BA⊥b,垂足为A.
计算方法:
先测量出QO、OA 、AB的长,
利用对应边成比例,列方程求解即可
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
依据相似三角形的判定定理,你能得到哪些构造方法呢?
P
b
(合理)
方法四:平行线法
Q
S
a
T
R
构造相似三角形的步骤:
(1)在过点 S作直线 a ,使a⊥PS,
计算方法:
先测量出QS 、ST 、QR的长,
利用对应边成比例,列方程求解
(2)在直线a上选择适当的点T , 连接PT 交 直线 b 于点R .
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
求解过程
如图,已知QS = 45 m, ST = 90 m, QR = 60 m,
求河的宽度 PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST.
∴ ,
即 ,
,
∴PQ×90=(PQ+45)×60.
P
Q
R
S
T
a
b
解得,PQ=90(m).
因此,河宽大约为90 m.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
反思
P
Q
R
S
T
a
b
利用相似三角形,解决了不能直接测量的物体的宽度或高度问题.
P
Q
O
b
B
A
构造方法:
保证包含“河宽”的三角形至少有一条边不需要跨河测量.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
反思
思考:如何测量池塘的宽度PQ呢?
P
Q
O
E
F
P
Q
O
E
F
你还有其他方法吗?
全等三角形法
中位线法
“全等三角形法” 与“中位线法” 是“相似三角形法”的特殊情形.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
利用相似三角形可以解决下面的2个问题
总结
测高:不易到达顶部,不能直接使用测量工具;
测距:不易直接测量的两点间的距离.
阅读问题
体会情境
抽象模型
构造相似
总结归纳
回归实际
画出图形
解决问题
一般步骤
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1.如图,左、右并排的两棵树的高分别是AB=8 m和CD=12 m,两树相距BD=5 m,一个人估计自己眼睛距地面的距离是EF=1.6 m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?
A
B
C
D
E
F
l
A
B
C
D
E
F
l
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
分析:如图1,设眼睛的位置为点F,
水平视线FG分别交AB,CD于点H,K.
∠AFH是观察点A时的仰角.
B
D
E
A
C
H
K
G
F
l
Ⅰ
Ⅱ
由于树的遮挡,区域Ⅰ是盲区.
同样地,∠CFK是观察点C时的仰角,
区域Ⅱ是盲区
图1
如图2,当某人从左向右移动过程中,
(1)当走到O点时,点F、A、C三点刚好共线
(临界位置),
O
(2)在点O的右边时,无法看到点C.
(3)在点O的左边时,可以看到点C.
图2
最近距离是BO
盲区
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
解:如图,假设观察者从左向右走到点O时,她的眼睛的位置点F与两棵树的顶端点A,C恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AFH∽△CFK.
∴ ,
A
B
C
D
E
F
l
O
最近距离是BO
H
K
G
∵AB=8 m、CD=12 m,
BD=5 m,OF=1.6 m
解得 FH=8(m).
由此可知,当她与左边的树的距离小于8 m时,她看不到右边树的顶端C.
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
数学建模思想:
把生活中的实际问题通过建模的思想,转化为数学问题来解决
一般步骤:
(1)根据题设中的已知量与未知量画出数学示意图,
(2)抽象出几何位置关系
(3)根据几何图形的知识解决实际问题.
A
B
C
D
F
l
O
H
K
G
该例题的关键是找到临界位置,满足F、A、C三点共线
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1. 如图,小明在 A 时测得某树的影长为 2 m,B 时又测得该树的影长为 8 m,若两次日照的光线互相垂直,则树的高度为____m.
A时
B时
A
B
C
D
解:设树的高度是x米,因为
4
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.小王同学,测树时发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7m,留在墙上部分的影长为1m,同时,小明测得长为1m的竹竿影长为0.9m.请计算这棵树的高.
1
分析:
利用相似三角形的知识解决.先构造出相似三角形,再列方程求解
1m
0.9m
由于太阳光线是平行线,所以,可以构成右图所示的相似三角形.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1
因此这棵树的高为4米.
解:过点D作 交AB于点F.
1m
0.9m
P
Q
R
A
B
C
D
F
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
思考:关于这道题你还有其他构造相似三角形的方法吗?
1m
0.9m
P
Q
R
方法一
A
B
C
D
F
1m
0.9m
P
Q
R
方法二
A
B
C
D
E
1
2.7
x
1m
0.9m
P
Q
R
方法三
A
B
C
D
F
2.7
x-1
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
测高与测距问题的解决方法:
测量河流的宽度的方法
构造相似三角形注意事项:
保证包含“河宽”的三角形至少有一条边不需要跨河测量.
利用相似三角形测量河宽
构造相似三角形:(1)8字型相似三角形;(2)平行线法相似三角形
P
Q
O
b
B
A
P
Q
R
S
T
a
b
通过构造相似三角形进行解决,根据不同的实际情况
选择合适的方法
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
