人教版九年级数学下册 27.2.3相似三角形的应用举例第1课时课件(共21张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.2.3相似三角形的应用举例第1课时课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 13:58:47 | ||
图片预览






文档简介
(共21张PPT)
相似三角形的应用举例
学习目标
通过构造相似三角形,列方程解决建筑物的高度,培养应用意识;
掌握构造相似三角形的三种常见方法,加深对相似三角形判定的理解;
体会构造相似三角形的方法与技巧,培养发现问题、解决问题的能力
4. 经历探究过程,体会把实际问题转化为数学问题的必要性和科学性,激发学生的学习兴趣,培养自信心.
重点
相似三角形的应用
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
你知道金字塔的高度是多少吗?据说是古希腊数学家、天文学家泰勒斯测算出来的.
泰勒斯
金字塔
金字塔100多米高,重500万吨
思考:请你思考一下泰勒斯是如何测算金字塔的高度的呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
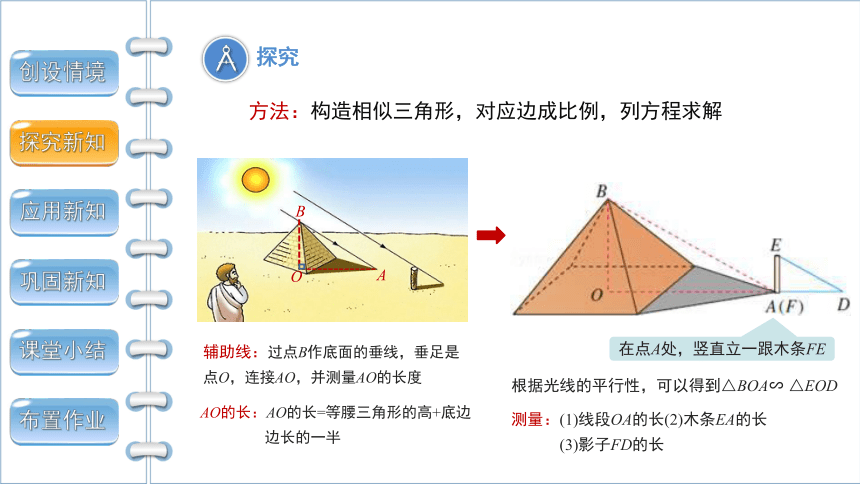
探究
辅助线:过点B作底面的垂线,垂足是点O,连接AO,并测量AO的长度
B
O
A
方法:构造相似三角形,对应边成比例,列方程求解
在点A处,竖直立一跟木条FE
根据光线的平行性,可以得到△BOA∽ △EOD
测量:(1)线段OA的长(2)木条EA的长
(3)影子FD的长
AO的长:AO的长=等腰三角形的高+底边
边长的一半
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图:木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
解:太阳光是平行光线,因此∠BAO=∠EDF,
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF.
∴ .
∴ (m).
因此金字塔的高度为134 m.
求解过程
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
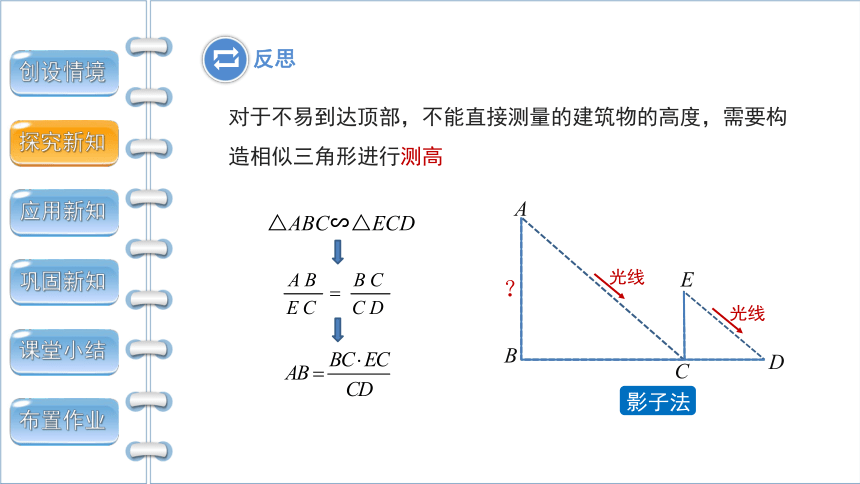
对于不易到达顶部,不能直接测量的建筑物的高度,需要构造相似三角形进行测高
反思
△ABC∽△ECD
光线
光线
A
B
C
D
E
?
影子法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
你能测量一下校园内旗杆的高度吗?
各小组完成该项探究作业.
(国旗底座的高度忽略不计)
实践探究作业单:
设计测量方案
写出需要测量的数据
计算结果
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
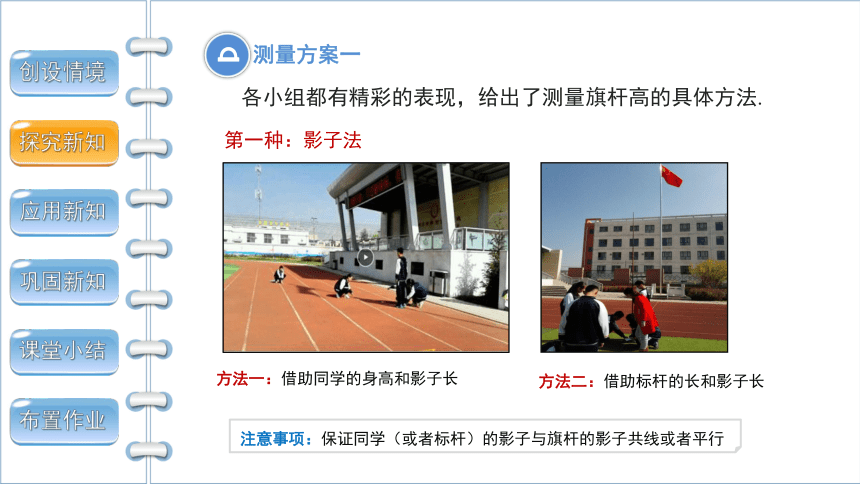
各小组都有精彩的表现,给出了测量旗杆高的具体方法.
第一种:影子法
方法一:借助同学的身高和影子长
方法二:借助标杆的长和影子长
测量方案一
注意事项:保证同学(或者标杆)的影子与旗杆的影子共线或者平行
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
光线
光线
A(旗杆顶端)
B
C
D
E(标杆顶端)
测试数据
方法一:利用同学的身高和影子长
方法二:利用标杆的长度和影子长
A
B
C
D (旗杆顶端)
F
E
光线
光线
测量的数据:
旗杆的影子EF长;
同学的身高AB长;同学的影子BC长
测量方案:
旗杆的影子BC长;
标杆的长度CE长;标杆的影子CD长
理由:△ABC∽△DEF(AA)
理由:△ABC∽△ECD(AA)
(共需要3个数据)
(共需要3个数据)
第一种:影子法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
第二种:目测法
(3)调整同学的位置,使同学的眼睛、标杆顶部、旗杆顶部在一条直线上
旗杆顶部
标杆顶部
A
B
C
测量方案:
(1)将标杆在点B处直立,旗杆底部记为点A
(2) 同学站在点C处,使A、B、C三点共线
思考:A、B、C三点为什么需要共线呢?
测量方案二
画出
图形
D(眼睛)
N
F(旗杆顶部)
E(标杆顶部)
M
C
B
A
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
测试数据
理由:
∵AF⊥ AC ,BE⊥ AC ,
∴AF∥ BE .
∴△EMD∽△FND.
∴ ,
将测量的数据代入,解方程即可求出旗杆的高度AF
测量的数据:
同学与标杆的底部的距离BC;
旗杆的影子长AC;
同学的眼睛与地面的距离CD;
标杆的长度BE.
(共需要4个数据)
D (眼睛)
N
F (旗杆顶部)
E (标杆顶部)
M
C
B
A
第二种:目测法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
第三种:镜子法
(3)调整同学的位置,使得刚好从镜子里面可以看到旗杆的顶部
测量方案:
(1)在地面上摆放一面镜子,
(2) 使得旗杆的底部、镜子、同学的位置成一条直线
(镜子)
1
2
思考:为什么一定要刚好看到旗杆的顶部呢?
测量方案三
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
测试数据
(镜子)
1
2
A (眼睛)
C (旗杆顶部)
E (镜子)
B
D
1
2
数据测量:
眼睛距离地面的高度AB,
镜子与同学的距离BE,
旗杆的影子长DE,
(共需要3个数据)
第三种:镜子法
理由:
根据光的反射原理,可得∠1=∠2
又∵∠B=∠D
∴△ABE∽△CDE.
∴ ,
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
上述三种方法,各有什么优缺点?你还有其他的测高方法吗?
A
B
C
D (旗杆顶端)
F
E
光线
光线
影子法
(眼睛) D
N
F (旗杆顶部)
E (标杆顶部)
M
C
B
A
目测法
镜子法
A (眼睛)
(旗杆顶部)C
E (镜子)
B
D
1
2
1、影子法需要测量3个数据,测量数据较少,但是需要依赖阳光和影子;
2、目测法不依赖影子,测量数据误差小,但需要的数据较多;
3、镜子法不依赖影子,但是镜子的角度有一点误差,就会导致结果的误差很大.
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1.在某一时刻,有人测得一高为1.8m的竹竿的影长为3m,某一楼的影长为60m,那么楼的高度是多少米?
解:设楼的高度是x m,根据相似三角形的性质,可得
答:楼的高度是100 m
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2.实践探究作业
请你设计一个方案,帮助家长测量一个物体的高.并完成下列问题
(1)使用的工具有哪些?
(2)测量的方法和步骤是怎样的?
(3)需要测量的数据有哪些?
(4)写出解答过程和结果
请以报告的形式上交作业.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
如图,小东用长为 3m 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,
竹竿与这一点相距 8 m、与旗杆相距 24 m,则旗杆的高为( )
A. 12m B. 10m C. 9m D. 7m
24m
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,电灯P在横杆AB的正上方,AB在
灯光下的影子为CD,AB∥CD,AB=2 m,
CD=5 m,点P到CD的距离是3 m,则点P到AB的距离是( )
A.
m
B.
m
C.
m
D.
m
C
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三种测高方法的优劣比较:
测量金字塔的高的方法:影子法
测高的方法:
(1)影子法 (2)目测法(3)镜子法
相似三角形的应用
利用立标杆的方法,借助太阳光线是平行线构造相似三角形
测高
(1)影子法需要3个数据,需要依赖太阳光线
(2)目测法需要4个数据,不需要依赖太阳光线
(3)镜子法需要3个数据,但如果镜子出现一点误差,结果的误差会很大
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
相似三角形的应用举例
学习目标
通过构造相似三角形,列方程解决建筑物的高度,培养应用意识;
掌握构造相似三角形的三种常见方法,加深对相似三角形判定的理解;
体会构造相似三角形的方法与技巧,培养发现问题、解决问题的能力
4. 经历探究过程,体会把实际问题转化为数学问题的必要性和科学性,激发学生的学习兴趣,培养自信心.
重点
相似三角形的应用
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
你知道金字塔的高度是多少吗?据说是古希腊数学家、天文学家泰勒斯测算出来的.
泰勒斯
金字塔
金字塔100多米高,重500万吨
思考:请你思考一下泰勒斯是如何测算金字塔的高度的呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
辅助线:过点B作底面的垂线,垂足是点O,连接AO,并测量AO的长度
B
O
A
方法:构造相似三角形,对应边成比例,列方程求解
在点A处,竖直立一跟木条FE
根据光线的平行性,可以得到△BOA∽ △EOD
测量:(1)线段OA的长(2)木条EA的长
(3)影子FD的长
AO的长:AO的长=等腰三角形的高+底边
边长的一半
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图:木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
解:太阳光是平行光线,因此∠BAO=∠EDF,
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF.
∴ .
∴ (m).
因此金字塔的高度为134 m.
求解过程
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
对于不易到达顶部,不能直接测量的建筑物的高度,需要构造相似三角形进行测高
反思
△ABC∽△ECD
光线
光线
A
B
C
D
E
?
影子法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
你能测量一下校园内旗杆的高度吗?
各小组完成该项探究作业.
(国旗底座的高度忽略不计)
实践探究作业单:
设计测量方案
写出需要测量的数据
计算结果
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
各小组都有精彩的表现,给出了测量旗杆高的具体方法.
第一种:影子法
方法一:借助同学的身高和影子长
方法二:借助标杆的长和影子长
测量方案一
注意事项:保证同学(或者标杆)的影子与旗杆的影子共线或者平行
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
光线
光线
A(旗杆顶端)
B
C
D
E(标杆顶端)
测试数据
方法一:利用同学的身高和影子长
方法二:利用标杆的长度和影子长
A
B
C
D (旗杆顶端)
F
E
光线
光线
测量的数据:
旗杆的影子EF长;
同学的身高AB长;同学的影子BC长
测量方案:
旗杆的影子BC长;
标杆的长度CE长;标杆的影子CD长
理由:△ABC∽△DEF(AA)
理由:△ABC∽△ECD(AA)
(共需要3个数据)
(共需要3个数据)
第一种:影子法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
第二种:目测法
(3)调整同学的位置,使同学的眼睛、标杆顶部、旗杆顶部在一条直线上
旗杆顶部
标杆顶部
A
B
C
测量方案:
(1)将标杆在点B处直立,旗杆底部记为点A
(2) 同学站在点C处,使A、B、C三点共线
思考:A、B、C三点为什么需要共线呢?
测量方案二
画出
图形
D(眼睛)
N
F(旗杆顶部)
E(标杆顶部)
M
C
B
A
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
测试数据
理由:
∵AF⊥ AC ,BE⊥ AC ,
∴AF∥ BE .
∴△EMD∽△FND.
∴ ,
将测量的数据代入,解方程即可求出旗杆的高度AF
测量的数据:
同学与标杆的底部的距离BC;
旗杆的影子长AC;
同学的眼睛与地面的距离CD;
标杆的长度BE.
(共需要4个数据)
D (眼睛)
N
F (旗杆顶部)
E (标杆顶部)
M
C
B
A
第二种:目测法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
第三种:镜子法
(3)调整同学的位置,使得刚好从镜子里面可以看到旗杆的顶部
测量方案:
(1)在地面上摆放一面镜子,
(2) 使得旗杆的底部、镜子、同学的位置成一条直线
(镜子)
1
2
思考:为什么一定要刚好看到旗杆的顶部呢?
测量方案三
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
测试数据
(镜子)
1
2
A (眼睛)
C (旗杆顶部)
E (镜子)
B
D
1
2
数据测量:
眼睛距离地面的高度AB,
镜子与同学的距离BE,
旗杆的影子长DE,
(共需要3个数据)
第三种:镜子法
理由:
根据光的反射原理,可得∠1=∠2
又∵∠B=∠D
∴△ABE∽△CDE.
∴ ,
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
上述三种方法,各有什么优缺点?你还有其他的测高方法吗?
A
B
C
D (旗杆顶端)
F
E
光线
光线
影子法
(眼睛) D
N
F (旗杆顶部)
E (标杆顶部)
M
C
B
A
目测法
镜子法
A (眼睛)
(旗杆顶部)C
E (镜子)
B
D
1
2
1、影子法需要测量3个数据,测量数据较少,但是需要依赖阳光和影子;
2、目测法不依赖影子,测量数据误差小,但需要的数据较多;
3、镜子法不依赖影子,但是镜子的角度有一点误差,就会导致结果的误差很大.
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1.在某一时刻,有人测得一高为1.8m的竹竿的影长为3m,某一楼的影长为60m,那么楼的高度是多少米?
解:设楼的高度是x m,根据相似三角形的性质,可得
答:楼的高度是100 m
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2.实践探究作业
请你设计一个方案,帮助家长测量一个物体的高.并完成下列问题
(1)使用的工具有哪些?
(2)测量的方法和步骤是怎样的?
(3)需要测量的数据有哪些?
(4)写出解答过程和结果
请以报告的形式上交作业.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
如图,小东用长为 3m 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,
竹竿与这一点相距 8 m、与旗杆相距 24 m,则旗杆的高为( )
A. 12m B. 10m C. 9m D. 7m
24m
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,电灯P在横杆AB的正上方,AB在
灯光下的影子为CD,AB∥CD,AB=2 m,
CD=5 m,点P到CD的距离是3 m,则点P到AB的距离是( )
A.
m
B.
m
C.
m
D.
m
C
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三种测高方法的优劣比较:
测量金字塔的高的方法:影子法
测高的方法:
(1)影子法 (2)目测法(3)镜子法
相似三角形的应用
利用立标杆的方法,借助太阳光线是平行线构造相似三角形
测高
(1)影子法需要3个数据,需要依赖太阳光线
(2)目测法需要4个数据,不需要依赖太阳光线
(3)镜子法需要3个数据,但如果镜子出现一点误差,结果的误差会很大
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
