人教版九年级数学下册 《29.3 课题学习 制作立体模型》教学课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学下册 《29.3 课题学习 制作立体模型》教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 755.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 14:11:54 | ||
图片预览






文档简介
(共17张PPT)
29.3 课题学习
制作立体模型
学习目标
通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程;
通过制作立体模型的实践活动,体会用三视图表示立体图形的作用;
通过经历实践活动的过程,进一步感受立体图形与平面图形之间的联系;
4. 通过该课题学习,增强学生学习数学的兴趣与信心.
重点
制作立体模型
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
活动一:
(1)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
思考:根据三视图,如何想象出实物图呢?
替换方案:
可以利用积木块儿或者马铃薯来制作模型
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究——活动一
活动一:
(1)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
分析:
1、主视图是弓形,物体的正面是圆形的一部分
3、左视图是正方形,说明模型的高度和宽度相等
2、俯视图是长方形,可以想到是模型是圆柱被平行于高的平面截后的一部分
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
(2)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
分析:
1、主视图是长方形,
3、左视图是正方形,说明模型的高度和宽度相等
2、俯视图是长方形加两个半圆形,可 以想到模型是棱柱和两边各半个圆柱的组合体
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
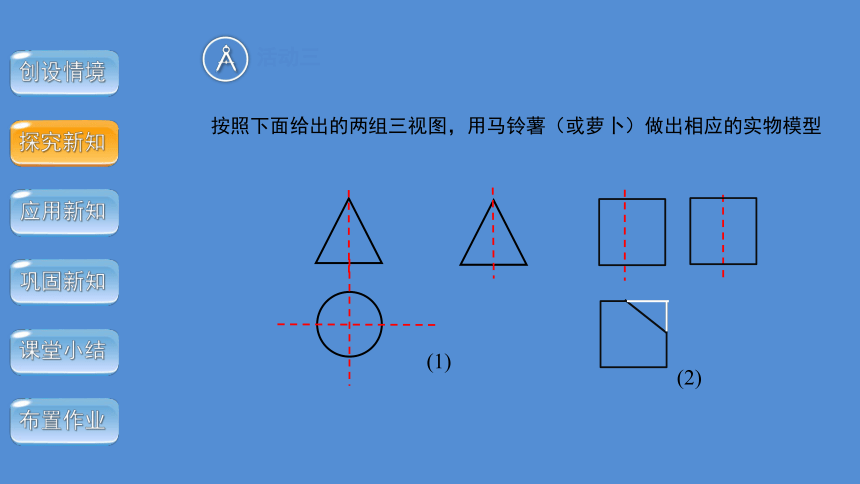
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(1)
(2)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(1)
(1)分析:
1、主视图是等腰三角形,可知实物是椎体
2、左视图是等腰三角形,可知实物是椎体
3、俯视图是圆形,可知模型是圆锥,如图:
实物模型为:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(2)分析:
1、根据三视图可以判断模型是正方体的一部分
2、结合虚线的位置和俯视图,确定正方体截取的位置
3、根据三视图,正确摆放模型,
(2)
实物模型为:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
提示:先尝试想象一下,猜想哪个图形可以折叠成三棱锥,
然后再试验一下,验证自己的猜想
下面的每一组平面图形都是由四个等边三角形组成.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
解:图(1)(3)可以折叠成三棱锥,如图
方法:以粉色三角形为底,
其余三角形向上折叠
方法:以粉色三角形为底, 紫色、蓝色三角形向上折叠,绿色三角形向后折叠即可
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
拓展:实际上,经过试验可知,图(1)(3)以任何颜色的三角形为底,都可以折叠成三棱锥.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
下面的每一组平面图形都是由四个等边三角形组成.
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
折叠
三视图
主视图
左视图
俯视图
注意:左视图是等腰三角形,其中腰等于等边三角形的高,底等于等边三角形边长
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
下面的每一组平面图形都是由四个等边三角形组成.
(3)如果图中小三角形的边长是1,那么对应的三棱锥的表面积是多少
(1)
(2)
(3)
解:三棱锥的表面积是:
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
在生活中,画出几个实物图的三视图,并且说明三视图中是怎样体现“长对正,高平齐,宽相等”的.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
画出正三棱锥的三视图
利用三视图还原实物图(1)
利用三视图还原实物图(2)
画三视图时,要根据三棱锥的摆放情况来画
制作立体模型
借助试验的方法,还原简单组合体的形状
借助试验的方法,还原不规则几何体的形状
布置作业
教科书习题3.3
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
29.3 课题学习
制作立体模型
学习目标
通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程;
通过制作立体模型的实践活动,体会用三视图表示立体图形的作用;
通过经历实践活动的过程,进一步感受立体图形与平面图形之间的联系;
4. 通过该课题学习,增强学生学习数学的兴趣与信心.
重点
制作立体模型
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
情境引入
活动一:
(1)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
思考:根据三视图,如何想象出实物图呢?
替换方案:
可以利用积木块儿或者马铃薯来制作模型
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究——活动一
活动一:
(1)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
分析:
1、主视图是弓形,物体的正面是圆形的一部分
3、左视图是正方形,说明模型的高度和宽度相等
2、俯视图是长方形,可以想到是模型是圆柱被平行于高的平面截后的一部分
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
(2)以硬纸板为主要材料,分别做出下面的三视图表示的立体模型
分析:
1、主视图是长方形,
3、左视图是正方形,说明模型的高度和宽度相等
2、俯视图是长方形加两个半圆形,可 以想到模型是棱柱和两边各半个圆柱的组合体
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(1)
(2)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(1)
(1)分析:
1、主视图是等腰三角形,可知实物是椎体
2、左视图是等腰三角形,可知实物是椎体
3、俯视图是圆形,可知模型是圆锥,如图:
实物模型为:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动二
按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型
(2)分析:
1、根据三视图可以判断模型是正方体的一部分
2、结合虚线的位置和俯视图,确定正方体截取的位置
3、根据三视图,正确摆放模型,
(2)
实物模型为:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
提示:先尝试想象一下,猜想哪个图形可以折叠成三棱锥,
然后再试验一下,验证自己的猜想
下面的每一组平面图形都是由四个等边三角形组成.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
解:图(1)(3)可以折叠成三棱锥,如图
方法:以粉色三角形为底,
其余三角形向上折叠
方法:以粉色三角形为底, 紫色、蓝色三角形向上折叠,绿色三角形向后折叠即可
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
(1)其中哪些可以折叠成三棱锥?把上面的图形描在纸上,剪下来,叠一叠,验证你的结论.
(1)
(2)
(3)
拓展:实际上,经过试验可知,图(1)(3)以任何颜色的三角形为底,都可以折叠成三棱锥.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
下面的每一组平面图形都是由四个等边三角形组成.
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
折叠
三视图
主视图
左视图
俯视图
注意:左视图是等腰三角形,其中腰等于等边三角形的高,底等于等边三角形边长
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
活动三
下面的每一组平面图形都是由四个等边三角形组成.
(3)如果图中小三角形的边长是1,那么对应的三棱锥的表面积是多少
(1)
(2)
(3)
解:三棱锥的表面积是:
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
在生活中,画出几个实物图的三视图,并且说明三视图中是怎样体现“长对正,高平齐,宽相等”的.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
画出正三棱锥的三视图
利用三视图还原实物图(1)
利用三视图还原实物图(2)
画三视图时,要根据三棱锥的摆放情况来画
制作立体模型
借助试验的方法,还原简单组合体的形状
借助试验的方法,还原不规则几何体的形状
布置作业
教科书习题3.3
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
