人教版八年级上册数学11.1.1三角形的边课时练习题(含答案)
文档属性
| 名称 | 人教版八年级上册数学11.1.1三角形的边课时练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 103.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览


文档简介
人教版八年级上册数学11.1.1三角形的边课时练习题(含答案)
一、单选题
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,10cm B.8cm,9cm,17cm
C.13cm,12cm,18cm D.5cm,5cm,11cm
2.下列长度的三条线段(单位:cm),能组成三角形的是()
A.1,4,7 B.2,5,8 C.3,6,9 D.4,7,10
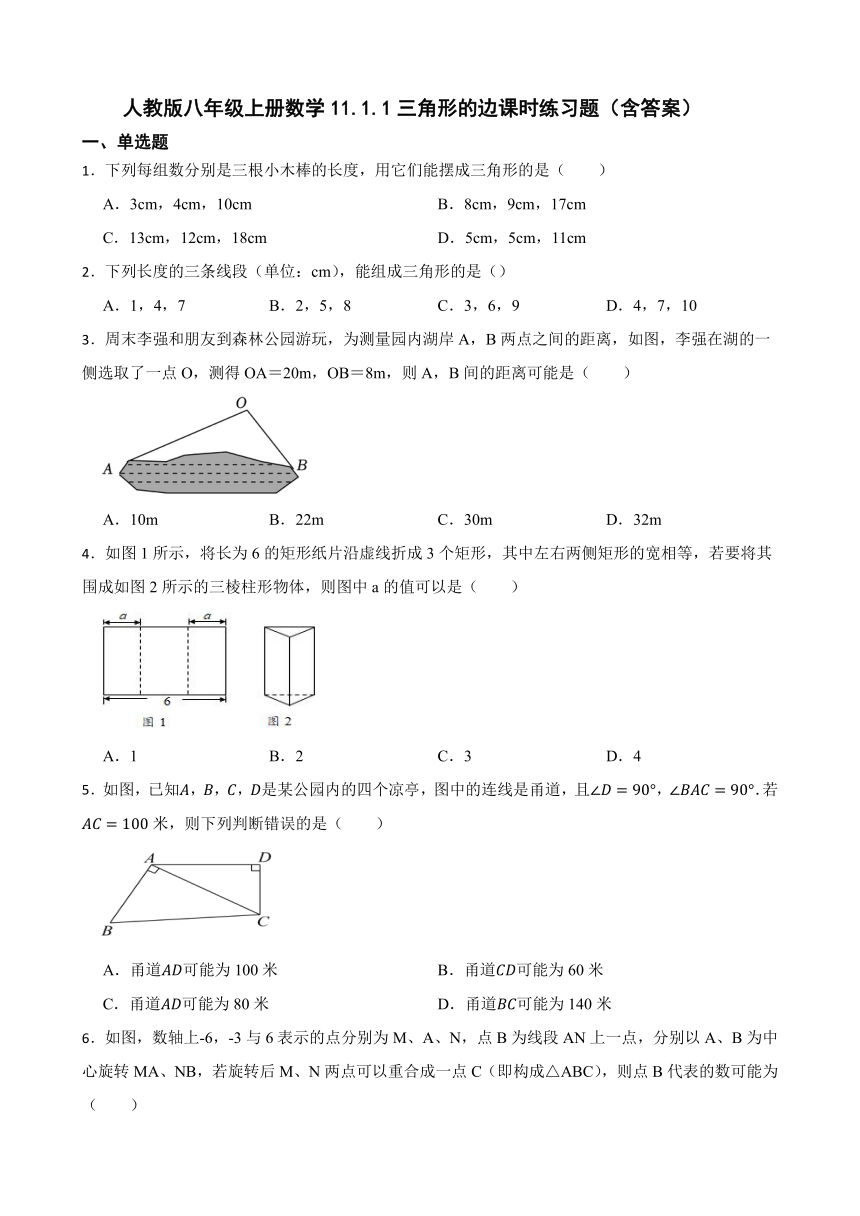
3.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
4.如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
A.1 B.2 C.3 D.4
5.如图,已知,,,是某公园内的四个凉亭,图中的连线是甬道,且,.若米,则下列判断错误的是( )
A.甬道可能为100米 B.甬道可能为60米
C.甬道可能为80米 D.甬道可能为140米
6.如图,数轴上-6,-3与6表示的点分别为M、A、N,点B为线段AN上一点,分别以A、B为中心旋转MA、NB,若旋转后M、N两点可以重合成一点C(即构成△ABC),则点B代表的数可能为( )
A.-1 B.0 C.2.5 D.3
7.若三角形两边长分别为7 cm和10 cm,则第三边长可能为( )
A.2 cm B.3 cm C.8 cm D.17 cm
8.如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( )
A.12米 B.10米 C.20米 D.8米
9.有一个三角形的两边长分别为2和5,则第三边的长可能是( )
A.2 B.2.5 C.3 D.5
10.线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )
A.3 B.4 C.5 D.6
11.如图,小华为估计水塘边A,B两点间的距离,在池塘同侧选取一点O,测出点O与点A间的距离为15米,点O与点B间的距离为10米,则AB长可能是( )
A.5米 B.15米 C.25米 D.30米
12.已知一个三角形的两边长分别为7和3,则这个三角形的第三边长可能是( )
A.3 B.4 C.9 D.12
二、填空题
13.边长为1的小正方形组成如图所示的6×6网格,点A,B,C,D,E,F,G,H都在格点上.其中到四边形ABCD四个顶点距离之和最小的点是 .
14.三角形的三边长为2,a,5,如果这个三角形中有两条边相等,那么它的周长是 .
15.已知a、b、c是的三边,则化简的结果是 .
16.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两个螺丝间的距离的最大值为 .
17.已知a、b、c是一个三角形的三条边长,则化简|a-b+c|-|a-b-c|=
18.若a,b,c是三角形的三边长,化简: .
19.三角形的两边长分别为4和6,那么第三边的取值范围是 .
20.三角形两边a=2,b=9,第三边c为为奇数,则此三角形周长为 .
21.已知某三角形的两条边长分别为4和9,则其第3三边的长可能是 .(写出一个即可)
22.如图,在平面直角坐标系中,点,C、D是y轴上的两个动点,且,连接AD、BC,则的最小值为 .
三、解答题
23.已知:a,b,c是三角形的三条边,化简:.
24.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
25.已知三角形的三边长分别为a,b,c,化简:.
26.若不等式组的解集是,
(1)求代数式的值;
(2)若a,b,c为某三角形的三边长,试求|c-a-b|+|c+3|的值.
答 案
1.C 2.D 3.B 4.B 5.A 6.C 7.C 8.C 9.D 10.A 11.B 12.C 13.E
14.12 15. 16.7 17. 18.2c-2b 19.2<a<10 20.20
21.9(答案不唯一) 22.5
23.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
24.解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
25.解:由题意得:,
,
,
,
,
.
26.解:,由①解得x<,由②解得x>2b-3,因为不等式组的解集为,所以=3,2b-3=-1,解得a=5,b=1,所以==0;
(1)解:,
由①解得x<,由②解得x>2b-3,
因为不等式组的解集为,
所以=3,2b-3=-1,
解得a=5,b=1,
所以==0;
(2)解:根据三角形的三边关系可知,4<c<6,
所以|c-a-b|+|c+3|=5+1-c+c-3=3.
一、单选题
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,10cm B.8cm,9cm,17cm
C.13cm,12cm,18cm D.5cm,5cm,11cm
2.下列长度的三条线段(单位:cm),能组成三角形的是()
A.1,4,7 B.2,5,8 C.3,6,9 D.4,7,10
3.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
4.如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
A.1 B.2 C.3 D.4
5.如图,已知,,,是某公园内的四个凉亭,图中的连线是甬道,且,.若米,则下列判断错误的是( )
A.甬道可能为100米 B.甬道可能为60米
C.甬道可能为80米 D.甬道可能为140米
6.如图,数轴上-6,-3与6表示的点分别为M、A、N,点B为线段AN上一点,分别以A、B为中心旋转MA、NB,若旋转后M、N两点可以重合成一点C(即构成△ABC),则点B代表的数可能为( )
A.-1 B.0 C.2.5 D.3
7.若三角形两边长分别为7 cm和10 cm,则第三边长可能为( )
A.2 cm B.3 cm C.8 cm D.17 cm
8.如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( )
A.12米 B.10米 C.20米 D.8米
9.有一个三角形的两边长分别为2和5,则第三边的长可能是( )
A.2 B.2.5 C.3 D.5
10.线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )
A.3 B.4 C.5 D.6
11.如图,小华为估计水塘边A,B两点间的距离,在池塘同侧选取一点O,测出点O与点A间的距离为15米,点O与点B间的距离为10米,则AB长可能是( )
A.5米 B.15米 C.25米 D.30米
12.已知一个三角形的两边长分别为7和3,则这个三角形的第三边长可能是( )
A.3 B.4 C.9 D.12
二、填空题
13.边长为1的小正方形组成如图所示的6×6网格,点A,B,C,D,E,F,G,H都在格点上.其中到四边形ABCD四个顶点距离之和最小的点是 .
14.三角形的三边长为2,a,5,如果这个三角形中有两条边相等,那么它的周长是 .
15.已知a、b、c是的三边,则化简的结果是 .
16.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两个螺丝间的距离的最大值为 .
17.已知a、b、c是一个三角形的三条边长,则化简|a-b+c|-|a-b-c|=
18.若a,b,c是三角形的三边长,化简: .
19.三角形的两边长分别为4和6,那么第三边的取值范围是 .
20.三角形两边a=2,b=9,第三边c为为奇数,则此三角形周长为 .
21.已知某三角形的两条边长分别为4和9,则其第3三边的长可能是 .(写出一个即可)
22.如图,在平面直角坐标系中,点,C、D是y轴上的两个动点,且,连接AD、BC,则的最小值为 .
三、解答题
23.已知:a,b,c是三角形的三条边,化简:.
24.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
25.已知三角形的三边长分别为a,b,c,化简:.
26.若不等式组的解集是,
(1)求代数式的值;
(2)若a,b,c为某三角形的三边长,试求|c-a-b|+|c+3|的值.
答 案
1.C 2.D 3.B 4.B 5.A 6.C 7.C 8.C 9.D 10.A 11.B 12.C 13.E
14.12 15. 16.7 17. 18.2c-2b 19.2<a<10 20.20
21.9(答案不唯一) 22.5
23.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
24.解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
25.解:由题意得:,
,
,
,
,
.
26.解:,由①解得x<,由②解得x>2b-3,因为不等式组的解集为,所以=3,2b-3=-1,解得a=5,b=1,所以==0;
(1)解:,
由①解得x<,由②解得x>2b-3,
因为不等式组的解集为,
所以=3,2b-3=-1,
解得a=5,b=1,
所以==0;
(2)解:根据三角形的三边关系可知,4<c<6,
所以|c-a-b|+|c+3|=5+1-c+c-3=3.
