2022-2023学年上学期湖南省益阳市多所学校期中联考七年级数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年上学期湖南省益阳市多所学校期中联考七年级数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 741.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 13:05:32 | ||
图片预览



文档简介
七年级数学期中测试
(试题卷)
满分:150分 时间:120分钟
姓名:___________班级:___________得分:___________
一、选择题(共40分)
1.四个数,0,1,3,其中负数是( )
A. B.0 C.1 D.3
2.下列各对数中,互为相反数的是( )
A.2与 B.和
C.与 D.与
3.新型冠状肺炎疫情发生以来,全国共有346支医疗队伍共计4.26万医护人员支援武汉和湖北,其中4.26万用科学记数法表示为( )
A.4.26×103 B.42.6×104 C.4.26×106 D.4.26×104
4.下列说法正确的是( )
A.0不是代数式 B.和都是多项式
C.的项分别是,,6 D.的次数是3
5.下列计算正确的是( )
A. B.
C. D.
6.下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由 ,得
7.某校进行100米跑步测试,男生合格标准定为15.5秒,体育老师记录了甲、乙、丙、丁四位男同学成绩如下表:(超出标准的部分记为“+”,不足标准的部分记为“-”),你认为100米跑步成绩最好的是( )
人员 甲 乙 丙 丁
成绩/秒
A.甲 B.乙 C.丙 D.丁
8.如图是一个简单的数值运算程序,若输入x的值为时,则输出的数值为( )
A. B. C.7 D.11
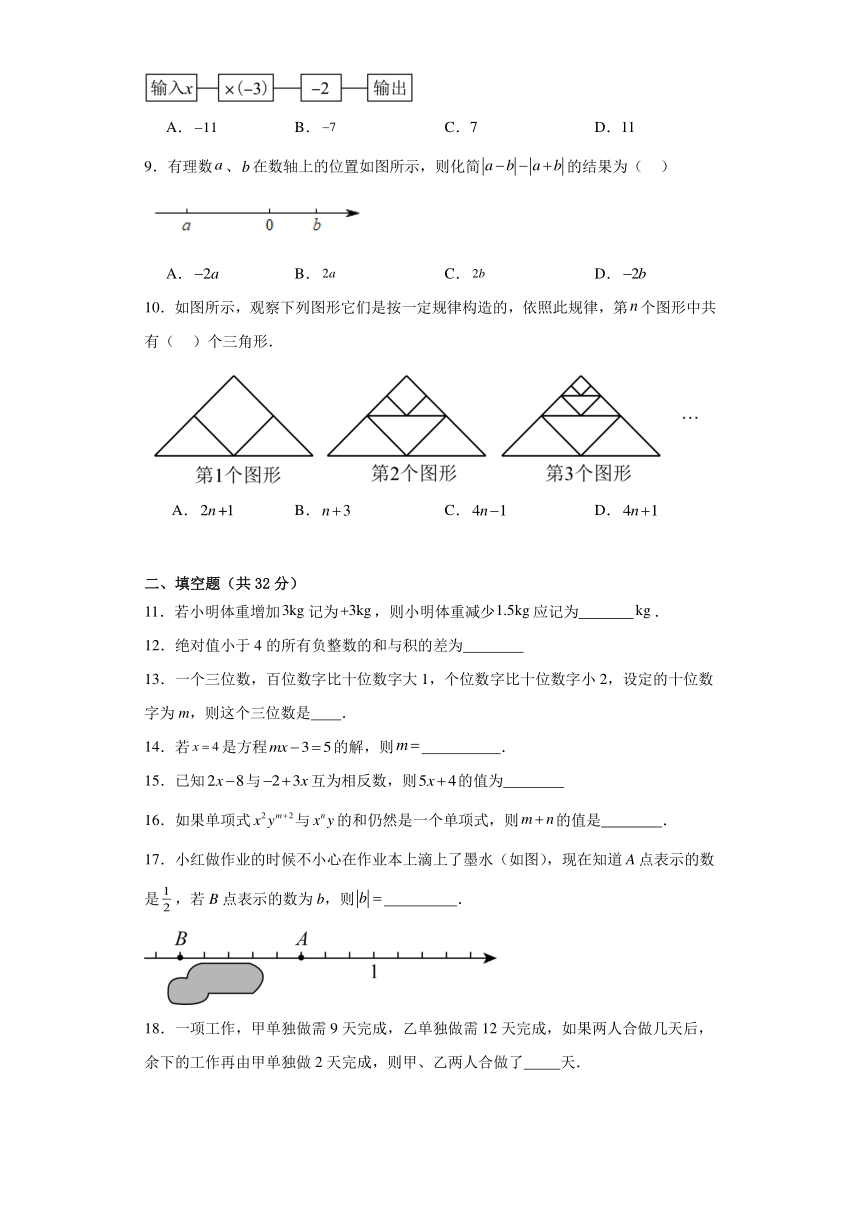
9.有理数、在数轴上的位置如图所示,则化简的结果为( )
A. B. C. D.
10.如图所示,观察下列图形它们是按一定规律构造的,依照此规律,第个图形中共有( )个三角形.
A. B. C. D.
二、填空题(共32分)
11.若小明体重增加记为,则小明体重减少应记为 .
12.绝对值小于4的所有负整数的和与积的差为
13.一个三位数,百位数字比十位数字大1,个位数字比十位数字小2,设定的十位数字为m,则这个三位数是 .
14.若是方程的解,则 .
15.已知与互为相反数,则的值为
16.如果单项式与的和仍然是一个单项式,则的值是 .
17.小红做作业的时候不小心在作业本上滴上了墨水(如图),现在知道A点表示的数是,若B点表示的数为b,则 .
18.一项工作,甲单独做需9天完成,乙单独做需12天完成,如果两人合做几天后,余下的工作再由甲单独做2天完成,则甲、乙两人合做了 天.
三、解答题(共78分)
19.
20.解方程:
21.先化简,再求值:,其中,.
22.老师在黑板上书写了一个正确的演算过程,随后用一张纸当住了一个二次三项式,形式如下:
(1)求被挡住的二次三项式;
(2)若,求所挡的二次三项式的值.
23.某工厂为满足市场需求计划每天生产600件防护服,如表是某一周的生产情况(超产部分记为正,减产部分记为负,单位:件).
星期 一 二 三 四 五 六 日
增减 +15 ﹣12 +10 ﹣15 ﹣8 +15 +20
(1)产量最多的一天比产量最少的一天多生产 件;
(2)该工厂实行计件工资制,每生产一件支付工资20元,本周该工厂应支付工人的工资总额是多少元?
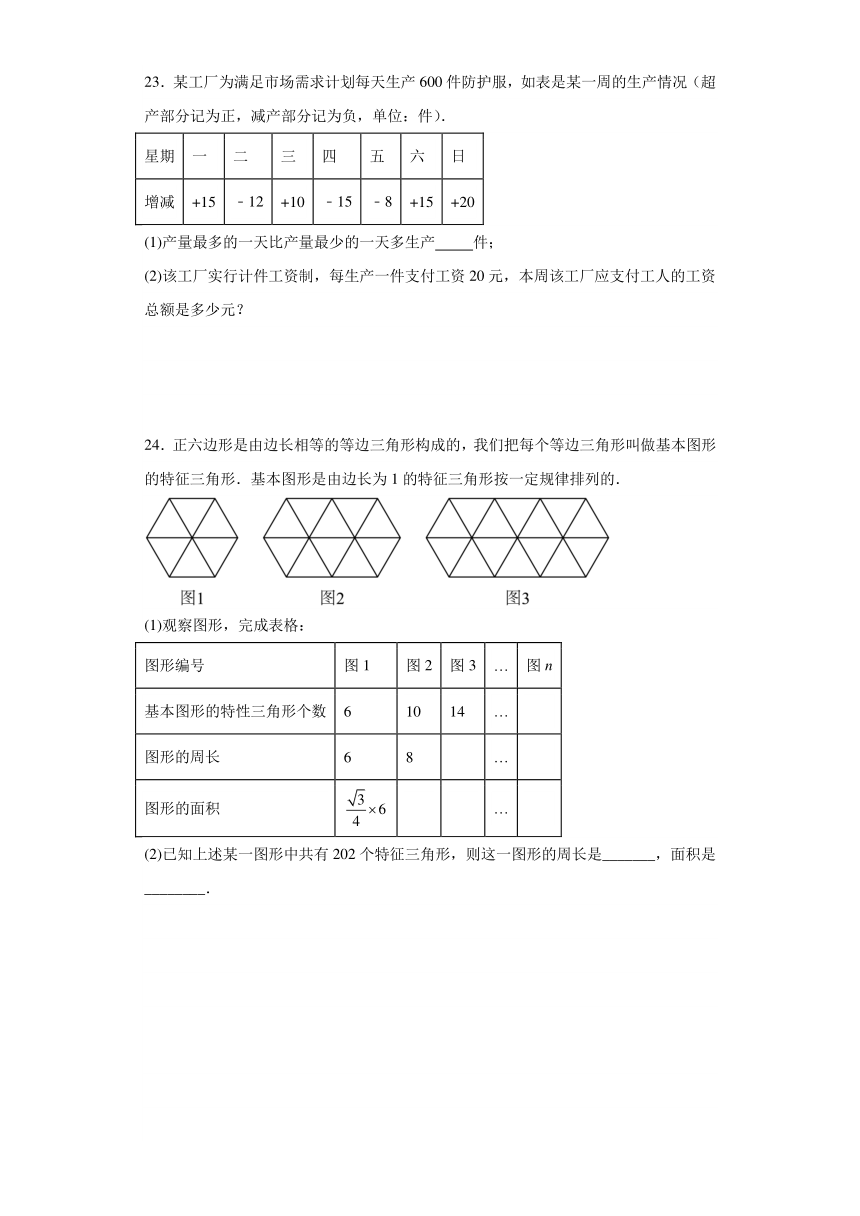
24.正六边形是由边长相等的等边三角形构成的,我们把每个等边三角形叫做基本图形的特征三角形.基本图形是由边长为1的特征三角形按一定规律排列的.
(1)观察图形,完成表格:
图形编号 图1 图2 图3 … 图n
基本图形的特性三角形个数 6 10 14 …
图形的周长 6 8 …
图形的面积 …
(2)已知上述某一图形中共有202个特征三角形,则这一图形的周长是_______,面积是________.
25.为丰富课后托管服务内容,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价70元,跳绳每条定价10元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条()
(1)若按A方案购买,一共需付款_________元(用含x的代数式表示);若按B方案购买,一共需付款_________元(用含x的代数式表示).
(2)购买跳绳条数为多少时,两种方案的收费相同?
(3)当时,你能设计出一种最省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
试卷第2页,共5页
参考答案
1.A
【分析】根据负数的意义即可得到答案.
【详解】∵,且小于零的数为负数,
∴为负数.
故选:A.
【点睛】此题考查了负数,熟练掌握负数的意义是解题的关键.
2.C
【分析】先分别计算每组中的两个数,再根据相反数的定义判断即可.
【详解】A. 2与不是相反数,故不符合题意;
B. =,故不符合题意;
C. ,,2与-2互为相反数,故符合题意;
D. ,, = ,故不符合题意.
故选:C
【点睛】本题主要考查了绝对值的性质,相反数的定义.熟练掌握以上知识是解题的关键.
3.D
【分析】用科学记数法表示绝对值大于1的数:.
【详解】解:.
故选:D.
【点睛】本题考查用科学记数法表示绝对值大于1的数.掌握相关结论即可.
4.D
【分析】根据代数式的定义可判断选项A;根据多项式的定义“几个单项式的和叫做多项式”可判断选项B;根据多项式的项的定义“每个单项式叫做多项式的项”可判断选项C;根据多项式的次数的定义“多项式里,次数最高项的次数,叫做这个多项式的次数”可判断选项D;即可得到答案.
【详解】解:A、0是代数式,故该选项说法错误,不符合题意;
B、不是多项式,是多项式,故该选项说法错误,不符合题意;
C、的项分别是,,,故该选项说法错误,不符合题意;
D、的最高项次项的次数是3次,所以的次数是3,故该选项说法正确,符合题意;
故选:D.
【点睛】本题考查了代数式和多项式,解题的关键是掌握代数式的定义和多项式的定义.
5.D
【分析】根据合并同类项的法则以及单项式乘以多项式运算法则进行计算后再判断即可.
【详解】A.和不是同类项,不能合并,计算错误,不符合题意;
B.和不是同类项,不能合并,计算错误,不符合题意;
C.,计算错误,不符合题意;
D.,正确,
故选:D.
【点睛】本题考查了合并同类项,掌握合并同类项法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变是解答本题的关键.
6.D
【分析】根据等式的基本性质逐项判断即可.
【详解】A、由,得,变形错误,该选项不符合题意;
B、由,得,变形错误,该选项不符合题意;
C、由,得,变形错误,该选项不符合题意;
D、变形正确,该选项符合题意.
故选:D.
【点睛】本题主要考查等式的基本性质,牢记等式的基本性质是解题的关键.
7.B
【分析】根据正负数的意义解答即可.
【详解】解:四位男同学成绩最好的是乙;
故选:B.
【点睛】本题考查学生对正数和负数的认识,弄清题意是解题的关键.
8.C
【分析】按照所给的计算法则求解即可.
【详解】解:,
故选C.
【点睛】本题主要考查了有理数的四则混合计算,正确理解题意是解题的关键.
9.C
【分析】根据有理数、在数轴上的位置可得,化简绝对值即可.
【详解】解:根据有理数、在数轴上的位置可得,
∴
,
故选:C.
【点睛】本题考查了在数轴上表示有理数,根据数轴判断式子的符号,化解绝对值等知识点,熟练掌握绝对值的意义以及数轴是解本题的关键.
10.C
【分析】根据所给图形中包含三角形的个数,找出数字的变化规律,列代数式即可.
【详解】解:观察所给图形可知:
第1个图形中有3个三角形,,
第2个图形中有7个三角形,,
第3个图形中有11个三角形,,
……
因此第个图形中共有个三角形.
故选C.
【点睛】本题考查用代数式表示数、图形的规律,解题的关键是从所给图形中找出数字的变化规律.
11.
【分析】“增加”和“减少”是具有相反意义的词语,因此“增加”记为“”时,减少记为“”.
【详解】体重增加记为,
体重减少记为.
故答案为:
【点睛】本题考查正负数意义的理解,用正负数表示两个具有相反意义的量;本题需要注意一个是意义相反,另一个就是它们表示的是数量.
12.
【分析】写出绝对值小于4的所有负整数,然后进行求和,求积,最后求差即可.
【详解】解:绝对值小于4的负整数有: 、 ,,
它们的和为: ,积为,
所以绝对值小于4的所有负整数的和与积的差为 ,
故答案为:.
【点睛】本题考查了绝对值,有理数的四则运算,熟练掌握运算法则是解题的关键.
13.111m+98.
【分析】先根据题意表示出百位和个位数字,再由“100×百位数字+10×十位数字+个位数字”得出这个三位数.
【详解】设十位数字为m,
则百位数字为m+1、个位数字为m-2,
所以这个三位数为100(m+1)+10m+m-2=111m+98,
故答案为111m+98.
【点睛】此题考查了代数式的列法,正确理解题意是解决此类题的关键.
14.2
【分析】将代入方程即可得到关于的一元一次方程,解方程即可得到答案.
【详解】解:是方程的解,
,
解得:,
故答案为:2.
【点睛】本题主要考查了一元一次方程的解,解一元一次方程,熟练掌握解一元一次方程的步骤,将代入方程是解题的关键.
15.
【分析】由互为相反数的两数之和为0列出方程,求出方程的解,再代入计算即可.
【详解】解:由题意得:,
解得:,
∴,
故答案为:.
【点睛】本题考查了相反数的定义,解一元一次方程,代数式求值,熟知互为相反数的两数之和为0是解题的关键.
16.1
【分析】所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.根据同类项的定义求解,即可得到答案.
【详解】解:单项式与的和仍然是一个单项式,
和是同类项,
,,
,
,
故答案为:1.
【点睛】本题考查了同类项定义,解题的键是掌握同类项定义中的两个“相同”:所含字母相同,相同字母的指数相同.
17.
【分析】A点表示的数是,从A点到1平均分了3份,据此可推出从A到0也是3份,可知从0到1一共平均分了6份,B点到原点是2份,即:,由此得到点B表示的数,再求出绝对值即可.
【详解】解:原点位置如图,
点B表示的数为:,
,
故答案为:.
【点睛】本题主要考查数轴和绝对值,关键是熟悉数轴的单位长度的意义.
18.4
【分析】设甲、乙两人合做了x天,甲单独做需9天完成,乙单独做需12天完成,则甲每天完成任务的,乙每天完成任务的,再由各部分的工作量之和等于总工作量列方程,解这个方程即可.
【详解】解:设甲、乙两人合做了x天,
可得方程:,
解得:,
答:甲、乙两人合做了4天.
故答案为:4.
【点睛】本题考查了一元一次方程的应用.列方程解应用题的关键是正确找出题目中的相等关系,用代数式表示出相等关系中的各个部分,把列方程的问题转化为列代数式的问题.
19.21
【分析】利用乘法分配律进行简便运算.
【详解】解:
【点睛】本题考查有理数的混合运算,掌握乘法分配律是解题的关键.
20.
【分析】依次去分母、去括号、移项、合并同类项、系数化1,即可解方程得到答案.
【详解】解:,
去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化1,得:.
【点睛】本题考查的是解一元一次方程,熟练掌握解一元一次方程的步骤是解题关键.
21.,
【分析】去括号,计算加减法,再将字母的值代入计算.
【详解】解:原式
当,时,原式.
【点睛】此题考查了整式的化简求值,正确掌握整式的计算法则是解题的关键.
22.(1)
(2)
【分析】(1)根据题意确定出所挡的二次三项式即可;
(2)把的值代入计算即可求出值.
【详解】(1)所挡的二次三项式为:;
(2)当时,原式.
【点睛】此题主要考查了整式的加减运算,根据加减法的关系逆推出所挡的二次三项式是解题的关键.
23.(1)35
(2)84500元
【分析】(1)根据正负数的意义确定星期日的产量最多,星期四的产量最少,然后用星期日的产量减去星期四的产量即可;
(2)求出一周产量的和,然后根据工资总额的计算方法,列式计算即可.
【详解】(1)(件),
∴产量最多的一天比产量最少的一天多生产35件,
故答案为:35.
(2)
(件),
(元),
∴本周该工厂应支付工人的工资总额是84500元.
【点睛】本题考查了正数和负数,理解“用正数和负数表示具有相反意义的量”是解决本题的关键.
24.(1),10,,,,
(2)104,
【分析】(1)根据题意探索规律求解;
(2)由(1)得出的规律,求出,进一步根据规律求解.
【详解】(1)第1个图形有三角形个,周长为,面积为,
第2个图形有三角形个,周长为,面积为,
第3个图形有三角形个,周长为,面积为,
……
第n个图形有三角形个,周长为,面积为
故答案为:,10,,,,
(2)由题意,
解得,
则该图形周长:,面积:
【点睛】本题考查探索图形规律,观察图形的组合,由最初的个例探索待求变量与序数的关系是解题的关键.
25.(1),
(2)购买150根跳绳时,A、B两种方案所需要的钱数一样多
(3)按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元
【分析】(1)由题意按A方案购买可列式:,在按B方案购买可列式:;
(2)由(1)列等式求解即可;
(3)先算全按同一种方案进行购买,计算出两种方案所需付款金额,再根据A方案是买一个篮球送跳绳,B方案是篮球和跳绳都按定价的付款,考虑可以按A方案买50个篮球,剩下的50条跳绳按B方案购买,计算出所需付款金额,进行比较即可.
【详解】(1)解:A方案购买可列式:元;
按B方案购买可列式:元;
故答案为:,;
(2)由(1)可知,
当A、B两种方案所需要的钱数一样多时,
即
解得.
答:购买150根跳绳时,A、B两种方案所需要的钱数一样多.
(3)当时,
按A方案购买需付款:(元);
按B方案购买需付款:(元);
按A方案购买50个篮球配送50个跳绳,按B方案购买50个跳绳合计需付款:
(元);
∵,
∴省钱的购买方案是:
按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元.
【点睛】此题考查的是列代数式并求值,也可作为一元一次方程来考查,因此做此类题需要掌握解应用题的能力.
答案第8页,共9页
(试题卷)
满分:150分 时间:120分钟
姓名:___________班级:___________得分:___________
一、选择题(共40分)
1.四个数,0,1,3,其中负数是( )
A. B.0 C.1 D.3
2.下列各对数中,互为相反数的是( )
A.2与 B.和
C.与 D.与
3.新型冠状肺炎疫情发生以来,全国共有346支医疗队伍共计4.26万医护人员支援武汉和湖北,其中4.26万用科学记数法表示为( )
A.4.26×103 B.42.6×104 C.4.26×106 D.4.26×104
4.下列说法正确的是( )
A.0不是代数式 B.和都是多项式
C.的项分别是,,6 D.的次数是3
5.下列计算正确的是( )
A. B.
C. D.
6.下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由 ,得
7.某校进行100米跑步测试,男生合格标准定为15.5秒,体育老师记录了甲、乙、丙、丁四位男同学成绩如下表:(超出标准的部分记为“+”,不足标准的部分记为“-”),你认为100米跑步成绩最好的是( )
人员 甲 乙 丙 丁
成绩/秒
A.甲 B.乙 C.丙 D.丁
8.如图是一个简单的数值运算程序,若输入x的值为时,则输出的数值为( )
A. B. C.7 D.11
9.有理数、在数轴上的位置如图所示,则化简的结果为( )
A. B. C. D.
10.如图所示,观察下列图形它们是按一定规律构造的,依照此规律,第个图形中共有( )个三角形.
A. B. C. D.
二、填空题(共32分)
11.若小明体重增加记为,则小明体重减少应记为 .
12.绝对值小于4的所有负整数的和与积的差为
13.一个三位数,百位数字比十位数字大1,个位数字比十位数字小2,设定的十位数字为m,则这个三位数是 .
14.若是方程的解,则 .
15.已知与互为相反数,则的值为
16.如果单项式与的和仍然是一个单项式,则的值是 .
17.小红做作业的时候不小心在作业本上滴上了墨水(如图),现在知道A点表示的数是,若B点表示的数为b,则 .
18.一项工作,甲单独做需9天完成,乙单独做需12天完成,如果两人合做几天后,余下的工作再由甲单独做2天完成,则甲、乙两人合做了 天.
三、解答题(共78分)
19.
20.解方程:
21.先化简,再求值:,其中,.
22.老师在黑板上书写了一个正确的演算过程,随后用一张纸当住了一个二次三项式,形式如下:
(1)求被挡住的二次三项式;
(2)若,求所挡的二次三项式的值.
23.某工厂为满足市场需求计划每天生产600件防护服,如表是某一周的生产情况(超产部分记为正,减产部分记为负,单位:件).
星期 一 二 三 四 五 六 日
增减 +15 ﹣12 +10 ﹣15 ﹣8 +15 +20
(1)产量最多的一天比产量最少的一天多生产 件;
(2)该工厂实行计件工资制,每生产一件支付工资20元,本周该工厂应支付工人的工资总额是多少元?
24.正六边形是由边长相等的等边三角形构成的,我们把每个等边三角形叫做基本图形的特征三角形.基本图形是由边长为1的特征三角形按一定规律排列的.
(1)观察图形,完成表格:
图形编号 图1 图2 图3 … 图n
基本图形的特性三角形个数 6 10 14 …
图形的周长 6 8 …
图形的面积 …
(2)已知上述某一图形中共有202个特征三角形,则这一图形的周长是_______,面积是________.
25.为丰富课后托管服务内容,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价70元,跳绳每条定价10元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条()
(1)若按A方案购买,一共需付款_________元(用含x的代数式表示);若按B方案购买,一共需付款_________元(用含x的代数式表示).
(2)购买跳绳条数为多少时,两种方案的收费相同?
(3)当时,你能设计出一种最省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
试卷第2页,共5页
参考答案
1.A
【分析】根据负数的意义即可得到答案.
【详解】∵,且小于零的数为负数,
∴为负数.
故选:A.
【点睛】此题考查了负数,熟练掌握负数的意义是解题的关键.
2.C
【分析】先分别计算每组中的两个数,再根据相反数的定义判断即可.
【详解】A. 2与不是相反数,故不符合题意;
B. =,故不符合题意;
C. ,,2与-2互为相反数,故符合题意;
D. ,, = ,故不符合题意.
故选:C
【点睛】本题主要考查了绝对值的性质,相反数的定义.熟练掌握以上知识是解题的关键.
3.D
【分析】用科学记数法表示绝对值大于1的数:.
【详解】解:.
故选:D.
【点睛】本题考查用科学记数法表示绝对值大于1的数.掌握相关结论即可.
4.D
【分析】根据代数式的定义可判断选项A;根据多项式的定义“几个单项式的和叫做多项式”可判断选项B;根据多项式的项的定义“每个单项式叫做多项式的项”可判断选项C;根据多项式的次数的定义“多项式里,次数最高项的次数,叫做这个多项式的次数”可判断选项D;即可得到答案.
【详解】解:A、0是代数式,故该选项说法错误,不符合题意;
B、不是多项式,是多项式,故该选项说法错误,不符合题意;
C、的项分别是,,,故该选项说法错误,不符合题意;
D、的最高项次项的次数是3次,所以的次数是3,故该选项说法正确,符合题意;
故选:D.
【点睛】本题考查了代数式和多项式,解题的关键是掌握代数式的定义和多项式的定义.
5.D
【分析】根据合并同类项的法则以及单项式乘以多项式运算法则进行计算后再判断即可.
【详解】A.和不是同类项,不能合并,计算错误,不符合题意;
B.和不是同类项,不能合并,计算错误,不符合题意;
C.,计算错误,不符合题意;
D.,正确,
故选:D.
【点睛】本题考查了合并同类项,掌握合并同类项法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变是解答本题的关键.
6.D
【分析】根据等式的基本性质逐项判断即可.
【详解】A、由,得,变形错误,该选项不符合题意;
B、由,得,变形错误,该选项不符合题意;
C、由,得,变形错误,该选项不符合题意;
D、变形正确,该选项符合题意.
故选:D.
【点睛】本题主要考查等式的基本性质,牢记等式的基本性质是解题的关键.
7.B
【分析】根据正负数的意义解答即可.
【详解】解:四位男同学成绩最好的是乙;
故选:B.
【点睛】本题考查学生对正数和负数的认识,弄清题意是解题的关键.
8.C
【分析】按照所给的计算法则求解即可.
【详解】解:,
故选C.
【点睛】本题主要考查了有理数的四则混合计算,正确理解题意是解题的关键.
9.C
【分析】根据有理数、在数轴上的位置可得,化简绝对值即可.
【详解】解:根据有理数、在数轴上的位置可得,
∴
,
故选:C.
【点睛】本题考查了在数轴上表示有理数,根据数轴判断式子的符号,化解绝对值等知识点,熟练掌握绝对值的意义以及数轴是解本题的关键.
10.C
【分析】根据所给图形中包含三角形的个数,找出数字的变化规律,列代数式即可.
【详解】解:观察所给图形可知:
第1个图形中有3个三角形,,
第2个图形中有7个三角形,,
第3个图形中有11个三角形,,
……
因此第个图形中共有个三角形.
故选C.
【点睛】本题考查用代数式表示数、图形的规律,解题的关键是从所给图形中找出数字的变化规律.
11.
【分析】“增加”和“减少”是具有相反意义的词语,因此“增加”记为“”时,减少记为“”.
【详解】体重增加记为,
体重减少记为.
故答案为:
【点睛】本题考查正负数意义的理解,用正负数表示两个具有相反意义的量;本题需要注意一个是意义相反,另一个就是它们表示的是数量.
12.
【分析】写出绝对值小于4的所有负整数,然后进行求和,求积,最后求差即可.
【详解】解:绝对值小于4的负整数有: 、 ,,
它们的和为: ,积为,
所以绝对值小于4的所有负整数的和与积的差为 ,
故答案为:.
【点睛】本题考查了绝对值,有理数的四则运算,熟练掌握运算法则是解题的关键.
13.111m+98.
【分析】先根据题意表示出百位和个位数字,再由“100×百位数字+10×十位数字+个位数字”得出这个三位数.
【详解】设十位数字为m,
则百位数字为m+1、个位数字为m-2,
所以这个三位数为100(m+1)+10m+m-2=111m+98,
故答案为111m+98.
【点睛】此题考查了代数式的列法,正确理解题意是解决此类题的关键.
14.2
【分析】将代入方程即可得到关于的一元一次方程,解方程即可得到答案.
【详解】解:是方程的解,
,
解得:,
故答案为:2.
【点睛】本题主要考查了一元一次方程的解,解一元一次方程,熟练掌握解一元一次方程的步骤,将代入方程是解题的关键.
15.
【分析】由互为相反数的两数之和为0列出方程,求出方程的解,再代入计算即可.
【详解】解:由题意得:,
解得:,
∴,
故答案为:.
【点睛】本题考查了相反数的定义,解一元一次方程,代数式求值,熟知互为相反数的两数之和为0是解题的关键.
16.1
【分析】所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.根据同类项的定义求解,即可得到答案.
【详解】解:单项式与的和仍然是一个单项式,
和是同类项,
,,
,
,
故答案为:1.
【点睛】本题考查了同类项定义,解题的键是掌握同类项定义中的两个“相同”:所含字母相同,相同字母的指数相同.
17.
【分析】A点表示的数是,从A点到1平均分了3份,据此可推出从A到0也是3份,可知从0到1一共平均分了6份,B点到原点是2份,即:,由此得到点B表示的数,再求出绝对值即可.
【详解】解:原点位置如图,
点B表示的数为:,
,
故答案为:.
【点睛】本题主要考查数轴和绝对值,关键是熟悉数轴的单位长度的意义.
18.4
【分析】设甲、乙两人合做了x天,甲单独做需9天完成,乙单独做需12天完成,则甲每天完成任务的,乙每天完成任务的,再由各部分的工作量之和等于总工作量列方程,解这个方程即可.
【详解】解:设甲、乙两人合做了x天,
可得方程:,
解得:,
答:甲、乙两人合做了4天.
故答案为:4.
【点睛】本题考查了一元一次方程的应用.列方程解应用题的关键是正确找出题目中的相等关系,用代数式表示出相等关系中的各个部分,把列方程的问题转化为列代数式的问题.
19.21
【分析】利用乘法分配律进行简便运算.
【详解】解:
【点睛】本题考查有理数的混合运算,掌握乘法分配律是解题的关键.
20.
【分析】依次去分母、去括号、移项、合并同类项、系数化1,即可解方程得到答案.
【详解】解:,
去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化1,得:.
【点睛】本题考查的是解一元一次方程,熟练掌握解一元一次方程的步骤是解题关键.
21.,
【分析】去括号,计算加减法,再将字母的值代入计算.
【详解】解:原式
当,时,原式.
【点睛】此题考查了整式的化简求值,正确掌握整式的计算法则是解题的关键.
22.(1)
(2)
【分析】(1)根据题意确定出所挡的二次三项式即可;
(2)把的值代入计算即可求出值.
【详解】(1)所挡的二次三项式为:;
(2)当时,原式.
【点睛】此题主要考查了整式的加减运算,根据加减法的关系逆推出所挡的二次三项式是解题的关键.
23.(1)35
(2)84500元
【分析】(1)根据正负数的意义确定星期日的产量最多,星期四的产量最少,然后用星期日的产量减去星期四的产量即可;
(2)求出一周产量的和,然后根据工资总额的计算方法,列式计算即可.
【详解】(1)(件),
∴产量最多的一天比产量最少的一天多生产35件,
故答案为:35.
(2)
(件),
(元),
∴本周该工厂应支付工人的工资总额是84500元.
【点睛】本题考查了正数和负数,理解“用正数和负数表示具有相反意义的量”是解决本题的关键.
24.(1),10,,,,
(2)104,
【分析】(1)根据题意探索规律求解;
(2)由(1)得出的规律,求出,进一步根据规律求解.
【详解】(1)第1个图形有三角形个,周长为,面积为,
第2个图形有三角形个,周长为,面积为,
第3个图形有三角形个,周长为,面积为,
……
第n个图形有三角形个,周长为,面积为
故答案为:,10,,,,
(2)由题意,
解得,
则该图形周长:,面积:
【点睛】本题考查探索图形规律,观察图形的组合,由最初的个例探索待求变量与序数的关系是解题的关键.
25.(1),
(2)购买150根跳绳时,A、B两种方案所需要的钱数一样多
(3)按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元
【分析】(1)由题意按A方案购买可列式:,在按B方案购买可列式:;
(2)由(1)列等式求解即可;
(3)先算全按同一种方案进行购买,计算出两种方案所需付款金额,再根据A方案是买一个篮球送跳绳,B方案是篮球和跳绳都按定价的付款,考虑可以按A方案买50个篮球,剩下的50条跳绳按B方案购买,计算出所需付款金额,进行比较即可.
【详解】(1)解:A方案购买可列式:元;
按B方案购买可列式:元;
故答案为:,;
(2)由(1)可知,
当A、B两种方案所需要的钱数一样多时,
即
解得.
答:购买150根跳绳时,A、B两种方案所需要的钱数一样多.
(3)当时,
按A方案购买需付款:(元);
按B方案购买需付款:(元);
按A方案购买50个篮球配送50个跳绳,按B方案购买50个跳绳合计需付款:
(元);
∵,
∴省钱的购买方案是:
按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元.
【点睛】此题考查的是列代数式并求值,也可作为一元一次方程来考查,因此做此类题需要掌握解应用题的能力.
答案第8页,共9页
同课章节目录
