直线与圆的位置关系(山东省东营市)
文档属性
| 名称 | 直线与圆的位置关系(山东省东营市) |  | |
| 格式 | rar | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-25 14:00:00 | ||
图片预览






文档简介
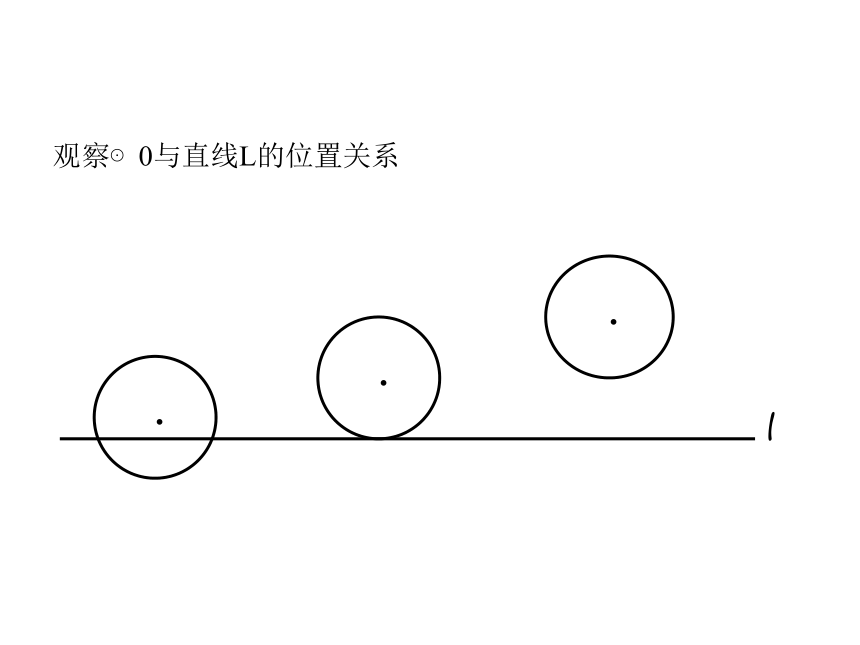
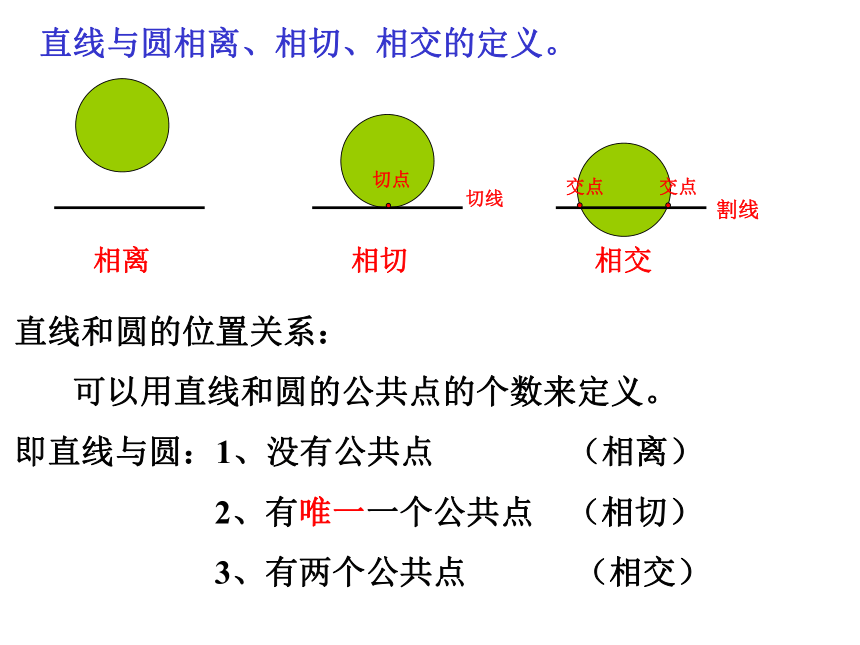
课件26张PPT。直线与圆的位置关系海上日出模拟:状态一:状态二:状态三:直线与圆相离、相切、相交的定义。直线和圆的位置关系:
可以用直线和圆的公共点的个数来定义。
即直线与圆:1、没有公共点 (相离)
2、有唯一一个公共点 (相切)
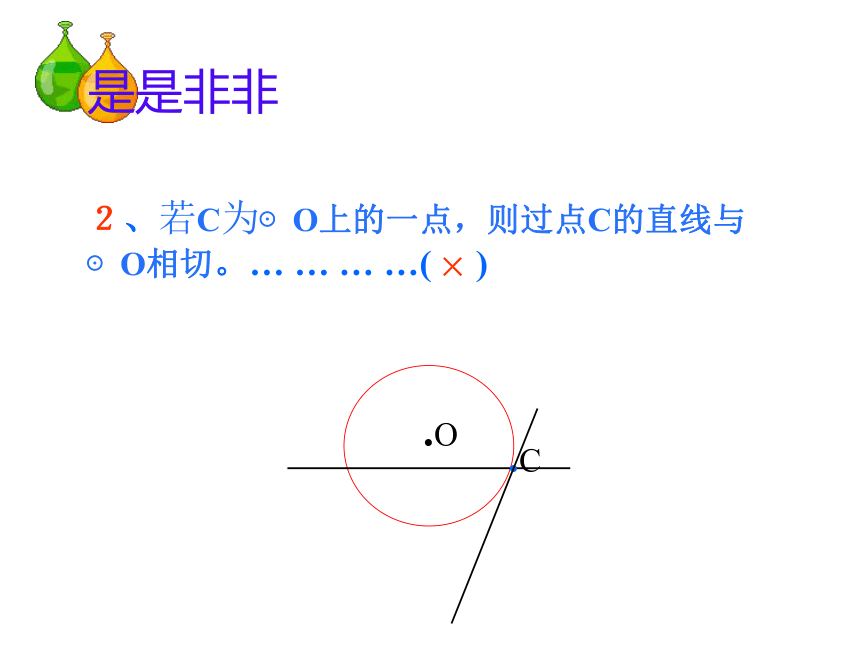
3、有两个公共点 (相交)相离相交相切切点切线割线是是非非 1、直线与圆最多有两个公共点 。( ) √是是非非×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )小问题:根据以上分析,我们可以怎样来判断直线与圆的位置关系? 直线与圆的公共点的个数新的问题:是否还有其它的方法来判断直线与圆的位置关系?ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d<
<
看一看想一想当直线与圆
相离、相切、
相交时,d与
r有何关系?lll.A.B.
C.D.E.F. NH.Q.d表示圆心O到直线l
的距离,r表示⊙O
的半径说说收获直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r无交点练 习 (一)1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。0相离1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系是……( )
A、相交 B、相切 C、相离 D、相切或相交CD练 习 (二).AO1、已知⊙A的直径为6,点A的坐标为(-3,-4),
则 ⊙A与X轴的位置关系是______,
⊙A与Y轴的位置关系是______。BC43相离相切练 习 (三)解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∴3×4 = 5×CD探讨:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足_______________时,
⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cmAC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想?当r满足_______________________
时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm(1)r=2cm; (2)r=4cm; (3)r=2.5cm.解:过点M作MN⊥OA于点N ∵在Rt△OMN中,∠AOB=30°,OM=5cm. ∴MN=2.5CM即圆心M到直线OA的距离d=2.5cm(1)当r=2cm时, ∵d> r,
∴⊙M与直线OA相离。(2)当r=4cm时, ∵d< r,
∴⊙M与直线OA相交。(3)当r=2.5cm时, ∵d = r,
∴⊙M与直线OA相切。 大家动手,做一做2.5cm1、直线与圆的位置关系有3种:相离、相切和相交。知识梳理 如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是 。思考题:希望大家如朝阳-蒸蒸日上
可以用直线和圆的公共点的个数来定义。
即直线与圆:1、没有公共点 (相离)
2、有唯一一个公共点 (相切)
3、有两个公共点 (相交)相离相交相切切点切线割线是是非非 1、直线与圆最多有两个公共点 。( ) √是是非非×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )小问题:根据以上分析,我们可以怎样来判断直线与圆的位置关系? 直线与圆的公共点的个数新的问题:是否还有其它的方法来判断直线与圆的位置关系?ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d
<
看一看想一想当直线与圆
相离、相切、
相交时,d与
r有何关系?lll.A.B.
C.D.E.F. NH.Q.d表示圆心O到直线l
的距离,r表示⊙O
的半径说说收获直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r无交点练 习 (一)1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。0相离1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系是……( )
A、相交 B、相切 C、相离 D、相切或相交CD练 习 (二).AO1、已知⊙A的直径为6,点A的坐标为(-3,-4),
则 ⊙A与X轴的位置关系是______,
⊙A与Y轴的位置关系是______。BC43相离相切练 习 (三)解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∴3×4 = 5×CD探讨:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足_______________时,
⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cm
以C为圆心,r为半径作圆。想一想?当r满足_______________________
时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
∴⊙M与直线OA相离。(2)当r=4cm时, ∵d< r,
∴⊙M与直线OA相交。(3)当r=2.5cm时, ∵d = r,
∴⊙M与直线OA相切。 大家动手,做一做2.5cm1、直线与圆的位置关系有3种:相离、相切和相交。知识梳理 如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是 。思考题:希望大家如朝阳-蒸蒸日上
同课章节目录
