空间几何体的结构(吉林省四平市)
文档属性
| 名称 | 空间几何体的结构(吉林省四平市) |  | |
| 格式 | rar | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-24 18:39:00 | ||
图片预览

文档简介
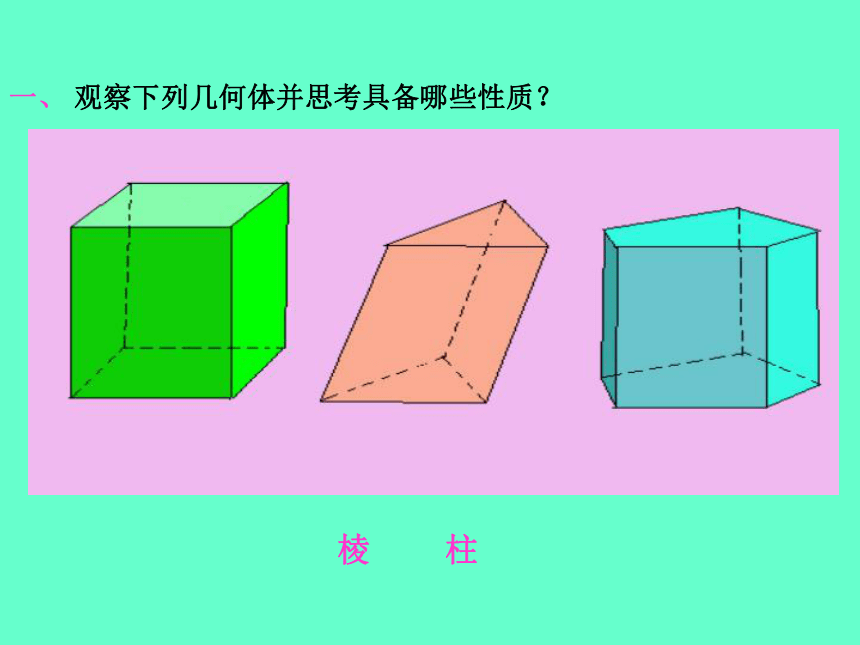
课件15张PPT。空间几何体的结构一、 观察下列几何体并思考具备哪些性质?棱 柱1、定义:有两个面互相平行,其余各面都是四边形,并且
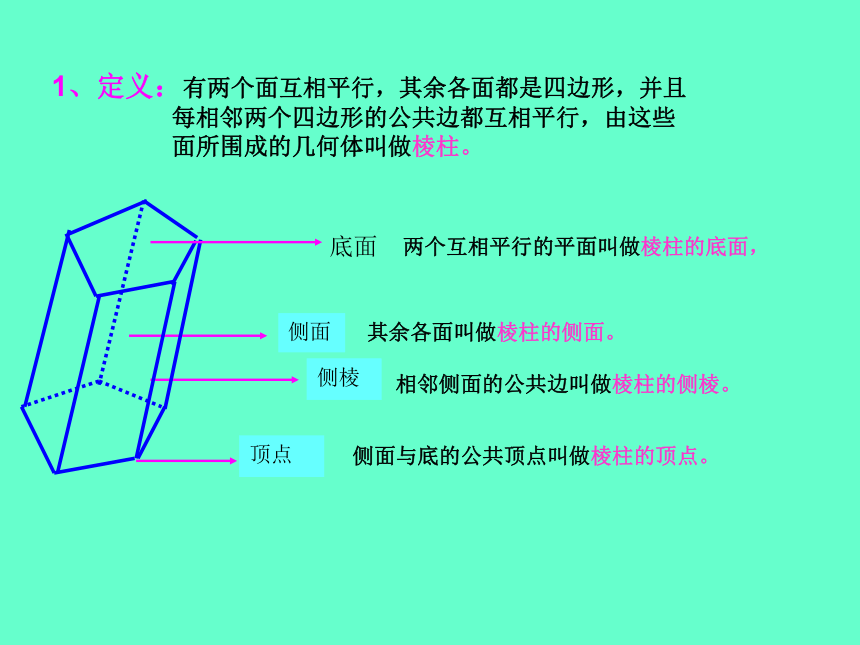
每相邻两个四边形的公共边都互相平行,由这些
面所围成的几何体叫做棱柱。
相邻侧面的公共边叫做棱柱的侧棱。 侧面与底的公共顶点叫做棱柱的顶点。 两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
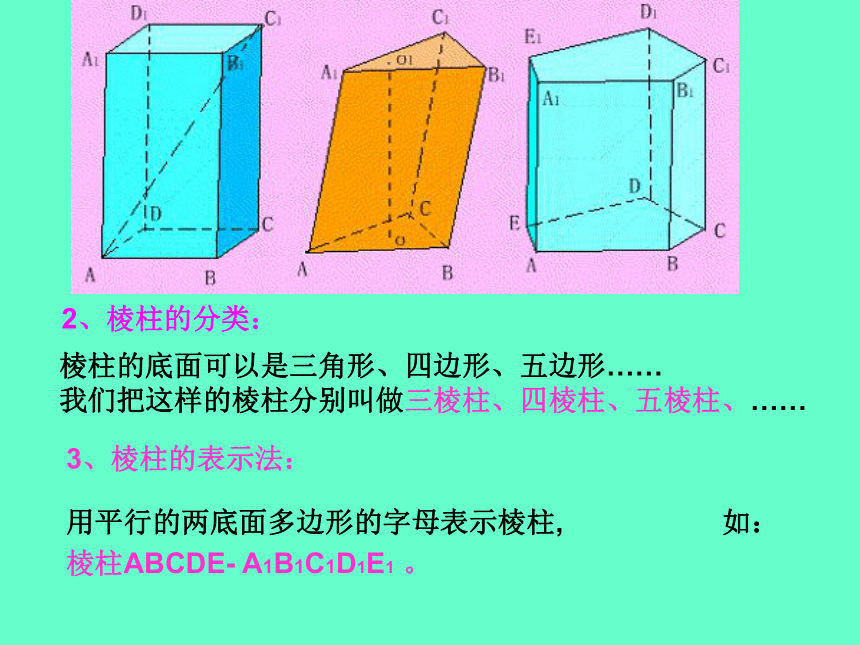
3、棱柱的表示法:用平行的两底面多边形的字母表示棱柱, 如:棱柱ABCDE- A1B1C1D1E1 。2、棱柱的分类: 棱柱的底面可以是三角形、四边形、五边形……
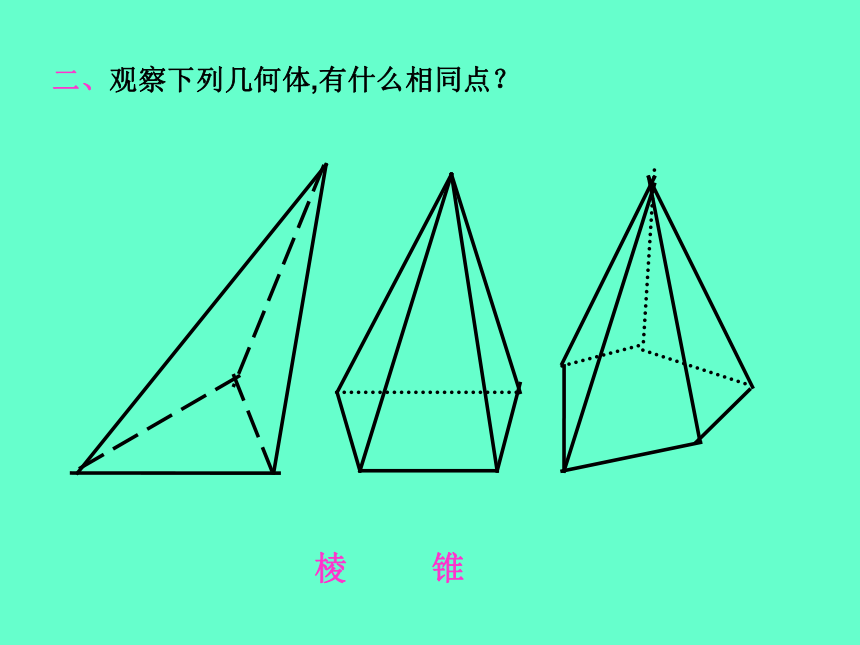
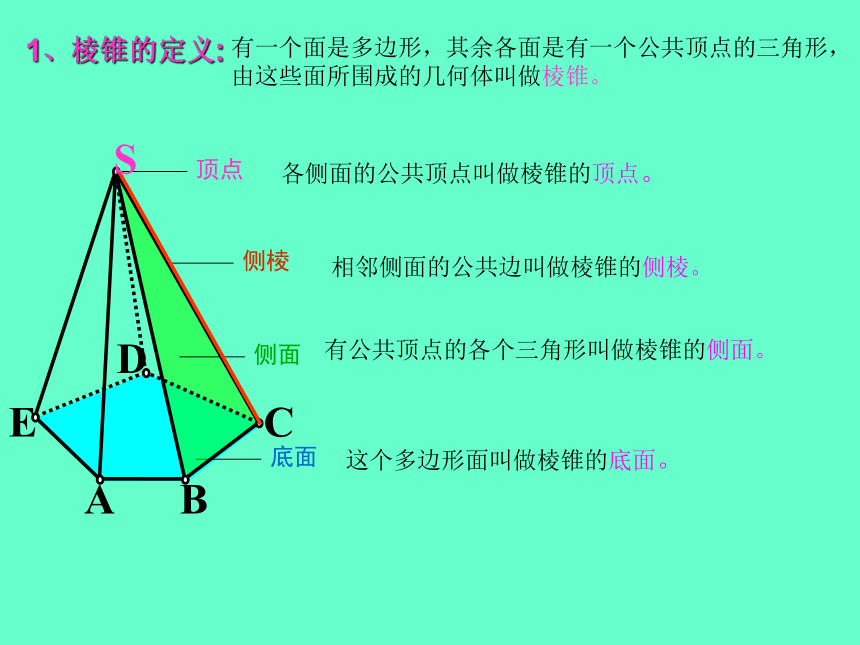
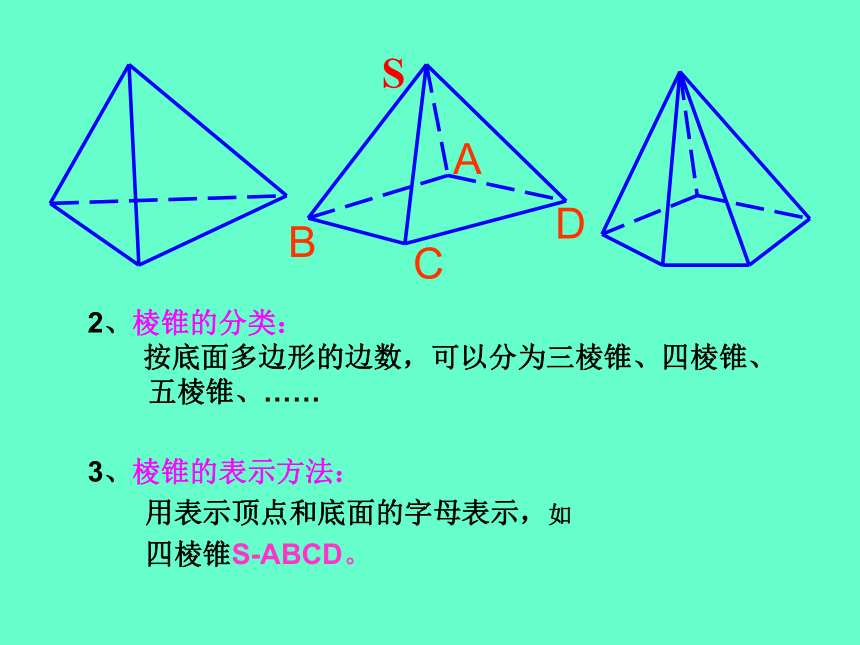
我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……二、观察下列几何体,有什么相同点?棱 锥1、棱锥的定义:有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。有公共顶点的各个三角形叫做棱锥的侧面。相邻侧面的公共边叫做棱锥的侧棱。 SABCDE各侧面的公共顶点叫做棱锥的顶点。2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、
五棱锥、……3、棱锥的表示方法:
用表示顶点和底面的字母表示,如
四棱锥S-ABCD。三、观察下列几何体的结构特征棱 台1、棱台的概念:用一个平行于棱锥底面的平面去截棱锥, 底面和截面之间的部分叫做棱台。2、棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,
分别叫做三棱台,四棱台,五棱台… 3、棱台的表示法:棱台用表示上、下底面各顶点的字母
来表示,如右图,棱台ABCD- A1B1C1D1
四、圆柱的结构特征1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。(1)旋转轴叫做圆柱的轴。(2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。(3)平行于轴的旋转而成的曲面叫做圆柱的侧面。(4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。2、圆柱表示:用表示它的轴的字母表示.3、圆柱与棱柱统称为柱体。如圆柱OO1 五、圆锥的结构特征:1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成曲面所围成的几何体叫做圆锥。(1)旋转轴叫做圆锥的轴。(2) 垂直于轴的边旋转而成的曲面叫做圆 锥的底面。(3)不垂直于轴的边旋转而成的曲面叫
做圆锥的侧面。(4)无论旋转到什么位置不垂直于轴的边都叫 做圆锥的母线。棱锥和圆锥统称为锥体六、圆台的结构特征1、定义:用一个平行于圆锥底面的平面去截圆锥,底 面与截之面间的部分,这样的几何体叫做圆台。2、圆台的表示:用表示它的轴的字母表示,如圆台OO′ 3、圆台与棱台统称为台体。七、球的结构特征 1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球心半径
我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……二、观察下列几何体,有什么相同点?棱 锥1、棱锥的定义:有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。有公共顶点的各个三角形叫做棱锥的侧面。相邻侧面的公共边叫做棱锥的侧棱。 SABCDE各侧面的公共顶点叫做棱锥的顶点。2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、
五棱锥、……3、棱锥的表示方法:
用表示顶点和底面的字母表示,如
四棱锥S-ABCD。三、观察下列几何体的结构特征棱 台1、棱台的概念:用一个平行于棱锥底面的平面去截棱锥, 底面和截面之间的部分叫做棱台。2、棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,
分别叫做三棱台,四棱台,五棱台… 3、棱台的表示法:棱台用表示上、下底面各顶点的字母
来表示,如右图,棱台ABCD- A1B1C1D1
四、圆柱的结构特征1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。(1)旋转轴叫做圆柱的轴。(2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。(3)平行于轴的旋转而成的曲面叫做圆柱的侧面。(4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。2、圆柱表示:用表示它的轴的字母表示.3、圆柱与棱柱统称为柱体。如圆柱OO1 五、圆锥的结构特征:1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成曲面所围成的几何体叫做圆锥。(1)旋转轴叫做圆锥的轴。(2) 垂直于轴的边旋转而成的曲面叫做圆 锥的底面。(3)不垂直于轴的边旋转而成的曲面叫
做圆锥的侧面。(4)无论旋转到什么位置不垂直于轴的边都叫 做圆锥的母线。棱锥和圆锥统称为锥体六、圆台的结构特征1、定义:用一个平行于圆锥底面的平面去截圆锥,底 面与截之面间的部分,这样的几何体叫做圆台。2、圆台的表示:用表示它的轴的字母表示,如圆台OO′ 3、圆台与棱台统称为台体。七、球的结构特征 1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球心半径
