11.1与三角形有关的线段 同步练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 11.1与三角形有关的线段 同步练习(含答案)2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 145.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 20:26:18 | ||
图片预览

文档简介
11.1与三角形有关的线段
一、选择题
1.下列各组线段中,能构成三角形的是( )
A.2,5,7 B.9,3,5 C.4,5,6 D.4,5,10
2.嘉兴某校项目化学习小组研究“三角形周长”的课题,将3根木棒首尾相连围成一个三角形,其中两根木棒的长分别为3cm、10cm,则该三角形的周长可能是( )
A.18cm B.19cm C.20cm D.21cm
3.下列各图中,正确画出 边上的高的是( )
A. B.
C. D.
4.已知中,,,则第三边AC的取值范围是( )
A. B. C. D.
5.如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )
A.三角形具有稳定性 B.两点确定一条直线
C.两点之间线段最短 D.三角形的两边之和大于第三边
6.如图,的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高为( )
A. B. C. D.
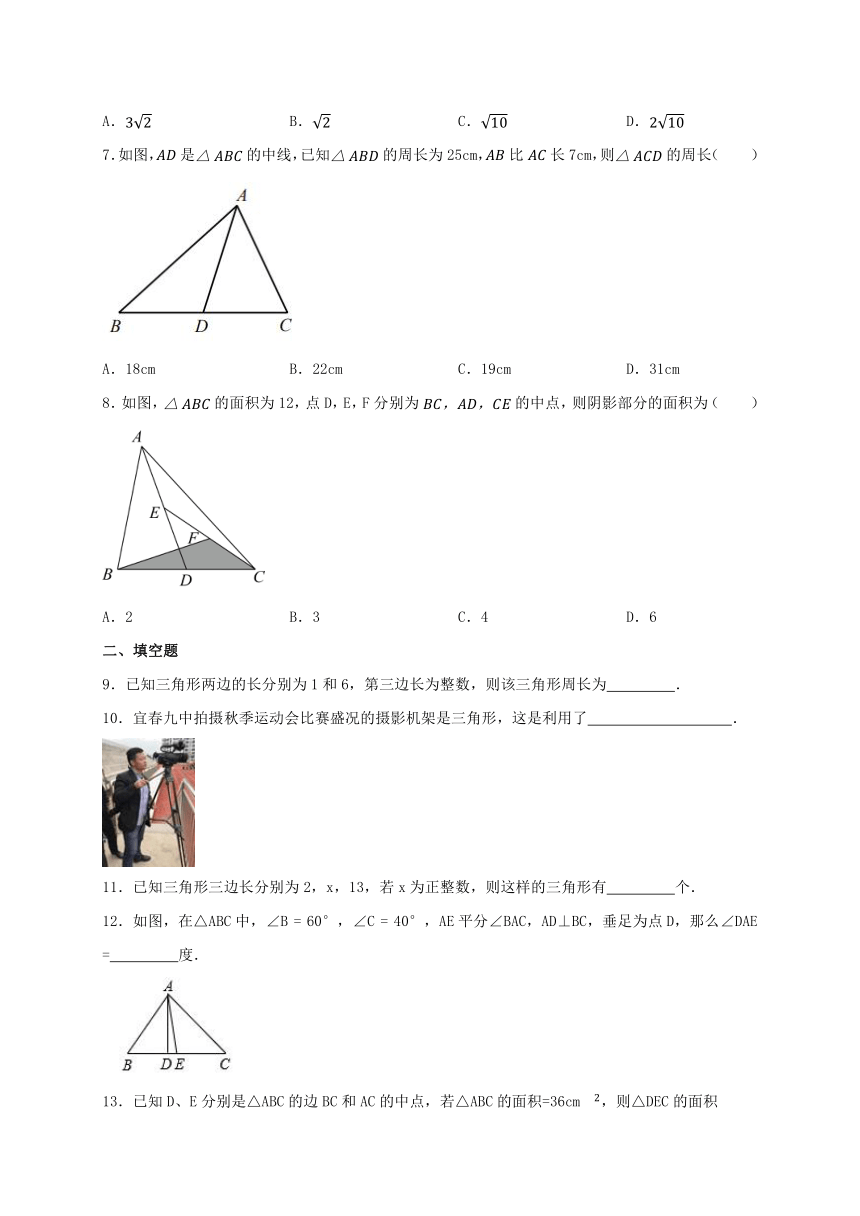
7.如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )
A.18cm B.22cm C.19cm D.31cm
8.如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( )
A.2 B.3 C.4 D.6
二、填空题
9.已知三角形两边的长分别为1和6,第三边长为整数,则该三角形周长为 .
10.宜春九中拍摄秋季运动会比赛盛况的摄影机架是三角形,这是利用了 .
11.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形有 个.
12.如图,在△ABC中,∠B = 60°,∠C = 40°,AE平分∠BAC,AD⊥BC,垂足为点D,那么∠DAE = 度.
13.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=36cm,则△DEC的面积为 .
三、解答题
14.已知:a,b,c是三角形的三条边,化简:.
15.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm.它的周长不超过37cm.求x的取值范围.
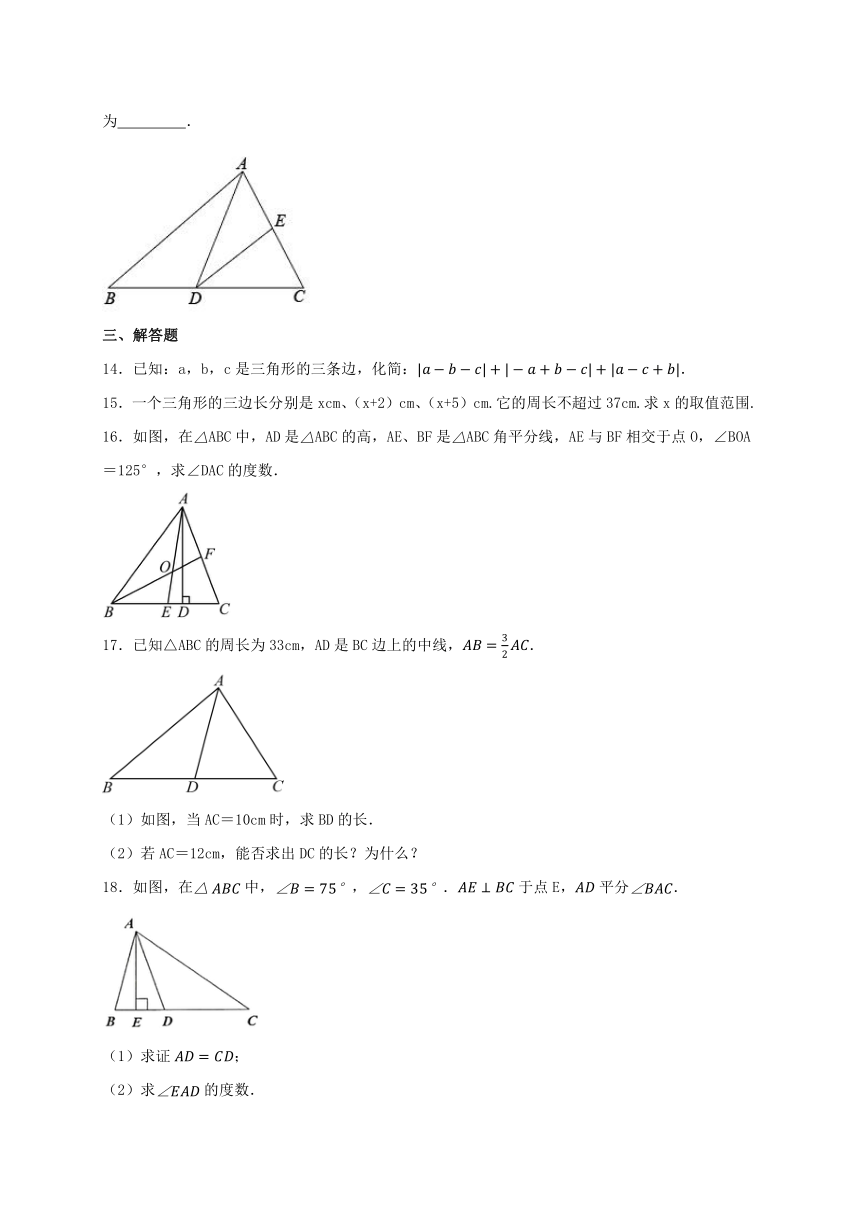
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,在中,,.于点E,平分.
(1)求证;
(2)求的度数.
参考答案
1.C
2.D
3.A
4.D
5.A
6.B
7.A
8.B
9.13
10.三角形的稳定性
11.3
12.10
13.9cm
14.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
15.解:∵一个三角形的三边长分别是xcm,(x+2)cm,(x+5)cm,它的周长不超过37cm,
∴ ,
解得:3<x≤10.
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)证明:∵,,
∴,
∵AD平分,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
即.
一、选择题
1.下列各组线段中,能构成三角形的是( )
A.2,5,7 B.9,3,5 C.4,5,6 D.4,5,10
2.嘉兴某校项目化学习小组研究“三角形周长”的课题,将3根木棒首尾相连围成一个三角形,其中两根木棒的长分别为3cm、10cm,则该三角形的周长可能是( )
A.18cm B.19cm C.20cm D.21cm
3.下列各图中,正确画出 边上的高的是( )
A. B.
C. D.
4.已知中,,,则第三边AC的取值范围是( )
A. B. C. D.
5.如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )
A.三角形具有稳定性 B.两点确定一条直线
C.两点之间线段最短 D.三角形的两边之和大于第三边
6.如图,的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高为( )
A. B. C. D.
7.如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )
A.18cm B.22cm C.19cm D.31cm
8.如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( )
A.2 B.3 C.4 D.6
二、填空题
9.已知三角形两边的长分别为1和6,第三边长为整数,则该三角形周长为 .
10.宜春九中拍摄秋季运动会比赛盛况的摄影机架是三角形,这是利用了 .
11.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形有 个.
12.如图,在△ABC中,∠B = 60°,∠C = 40°,AE平分∠BAC,AD⊥BC,垂足为点D,那么∠DAE = 度.
13.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=36cm,则△DEC的面积为 .
三、解答题
14.已知:a,b,c是三角形的三条边,化简:.
15.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm.它的周长不超过37cm.求x的取值范围.
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,在中,,.于点E,平分.
(1)求证;
(2)求的度数.
参考答案
1.C
2.D
3.A
4.D
5.A
6.B
7.A
8.B
9.13
10.三角形的稳定性
11.3
12.10
13.9cm
14.解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
15.解:∵一个三角形的三边长分别是xcm,(x+2)cm,(x+5)cm,它的周长不超过37cm,
∴ ,
解得:3<x≤10.
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)证明:∵,,
∴,
∵AD平分,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
即.
