22.3 实际问题与二次函数 同步练习(含简单答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习(含简单答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 527.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览


文档简介
22.3实际问题与二次函数
一、单选题
1.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
3.某企业的销售利润原来是m万元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y 与x的函数关系式是( )
A.y=x+m B.y=m(x-1) C.y=m(1+x) D.y=m(1-x)
4.在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为,由此可知小宇此次训练实心球落地时的水平距离为( )
A.85米 B.8米 C.10米 D.2米
5.如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=4,点E,G同时从点A出发,分别以每秒个单位的速度在射线AB,AC上运动,设运动时间为x秒,以点A为顶点的正方形AEFG与等腰直角三角形ABC重叠部分的面积为y,则大致能反映y与x之间的函数关系的图象为( )
A. B. C.D.
6.某班计划在劳动实践基地内种植蔬菜,班长买回来米长的围栏,准备围成两边靠墙(两墙垂直且足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(两直角边靠墙)、扇形这三种方案,如图所示.最佳方案是( )
A.方案1 B.方案2 C.方案1或方案2 D.方案3
7.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面的距离为;
④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为.
其中结论错误的是( )
A.① B.② C.③ D.④
8.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
9.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为( )件.
降价(元)
日销量(件)
A.1200 B.750 C.1110 D.1140
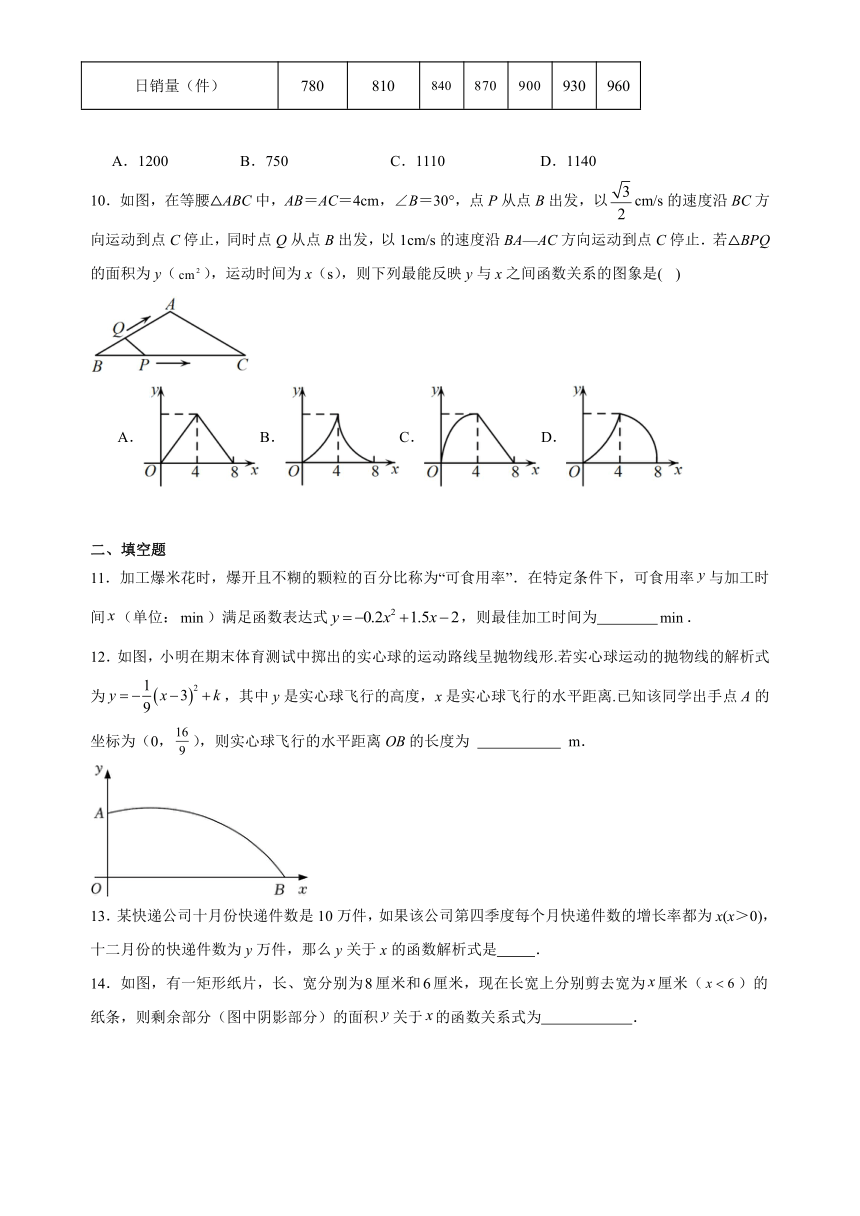
10.如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA—AC方向运动到点C停止.若△BPQ的面积为y(),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.B.C.D.
二、填空题
11.加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率与加工时间(单位:)满足函数表达式,则最佳加工时间为 .
12.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 m.
13.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
14.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
15.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是 m.
16.如图,一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离与时间的数据如下表.那么与之间的函数关系式是 .
时间 …
距离 …
三、解答题
17.某超市购进了一种商品,进价为每件8元,销售过程中发现,该商品每天的销售量(件)与每件售价(元)之间存在某种函数关系(其中,且为整数),且当时,;当时,;当时,;…,设超市销售这种消毒用品每天获利为(元).
(1)请判断与符合哪种函数关系,并求与的函数表达式;
(2)若该商店销售这种商品每天获润480元,则每件商品的售价为多少元;
(3)当每件商品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
18.某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间有如表关系:
销售单价x(元) 30 35 40 ┄ 70 ┄
每天的销售量y(件) 100 90 80 ┄ 20 ┄
(1)求该商品每天的销售量y与销售单价x之间的函数关系式;
(2)若商店按照单价不低于成本价,且不高于50元销售,则销售单价x定为多少才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)该商店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为保证捐款后销售该商品每天获得的利润不低于650元,则每天的销售量最少应为多少件?
19.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
20.在平面直角坐标系xOy中,已知直线与x轴,y轴分别交于点A,B,抛物线经过点A,将点B向右平移5个单位长度,得到点C.
(1)求C点坐标;
(2)求抛物线对称轴;
(3)若抛物线与线段BC有一个公共点,结合图像,求a的取值范围.
参考答案:
1.C
2.A
3.C
4.B
5.B
6.D
7.D
8.D
9.C
10.D
11.3.75
12.8
13.y=10(x+1)2
14.
15.5
16.
17.(1)一次函数;(2)14(3)15;525
18.(1)y=-2x+160;(2)50元,1200元;(3)20件
19.(1)(36-3x)(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
20.(1)C(5,3)(2)(3)a≥或a<-1或a=-
一、单选题
1.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10 B.20 C.30 D.10或30
3.某企业的销售利润原来是m万元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y 与x的函数关系式是( )
A.y=x+m B.y=m(x-1) C.y=m(1+x) D.y=m(1-x)
4.在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为,由此可知小宇此次训练实心球落地时的水平距离为( )
A.85米 B.8米 C.10米 D.2米
5.如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=4,点E,G同时从点A出发,分别以每秒个单位的速度在射线AB,AC上运动,设运动时间为x秒,以点A为顶点的正方形AEFG与等腰直角三角形ABC重叠部分的面积为y,则大致能反映y与x之间的函数关系的图象为( )
A. B. C.D.
6.某班计划在劳动实践基地内种植蔬菜,班长买回来米长的围栏,准备围成两边靠墙(两墙垂直且足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(两直角边靠墙)、扇形这三种方案,如图所示.最佳方案是( )
A.方案1 B.方案2 C.方案1或方案2 D.方案3
7.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面的距离为;
④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为.
其中结论错误的是( )
A.① B.② C.③ D.④
8.如图,晓波家的院墙一边靠墙处,用米长的铁栅栏围成了三个相连的养殖小院子,总面积为平方米,为方便喂养这些不同类的动物,在各个养殖院子之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则关于的函数关系式为( )
A. B.
C. D.
9.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为( )件.
降价(元)
日销量(件)
A.1200 B.750 C.1110 D.1140
10.如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA—AC方向运动到点C停止.若△BPQ的面积为y(),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.B.C.D.
二、填空题
11.加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率与加工时间(单位:)满足函数表达式,则最佳加工时间为 .
12.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 m.
13.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
14.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
15.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是 m.
16.如图,一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离与时间的数据如下表.那么与之间的函数关系式是 .
时间 …
距离 …
三、解答题
17.某超市购进了一种商品,进价为每件8元,销售过程中发现,该商品每天的销售量(件)与每件售价(元)之间存在某种函数关系(其中,且为整数),且当时,;当时,;当时,;…,设超市销售这种消毒用品每天获利为(元).
(1)请判断与符合哪种函数关系,并求与的函数表达式;
(2)若该商店销售这种商品每天获润480元,则每件商品的售价为多少元;
(3)当每件商品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
18.某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间有如表关系:
销售单价x(元) 30 35 40 ┄ 70 ┄
每天的销售量y(件) 100 90 80 ┄ 20 ┄
(1)求该商品每天的销售量y与销售单价x之间的函数关系式;
(2)若商店按照单价不低于成本价,且不高于50元销售,则销售单价x定为多少才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)该商店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为保证捐款后销售该商品每天获得的利润不低于650元,则每天的销售量最少应为多少件?
19.园林部门计划在某公园建一个长方形苗圃.苗圃的一面靠墙(墙最大可用长度为14米).另三边用木栏围成,中间也用垂直于墙的木栏隔开,分成两个区域,并在如图所示的两处各留2米宽的门(门不用木栏),建成后所用木栏总长32米,设苗圃的一边长为x米.
(1)长为________米(包含门宽,用含x的代数式表示);
(2)若苗圃的面积为,求x的值;
(3)当x为何值时,苗圃的面积最大,最大面积为多少?
20.在平面直角坐标系xOy中,已知直线与x轴,y轴分别交于点A,B,抛物线经过点A,将点B向右平移5个单位长度,得到点C.
(1)求C点坐标;
(2)求抛物线对称轴;
(3)若抛物线与线段BC有一个公共点,结合图像,求a的取值范围.
参考答案:
1.C
2.A
3.C
4.B
5.B
6.D
7.D
8.D
9.C
10.D
11.3.75
12.8
13.y=10(x+1)2
14.
15.5
16.
17.(1)一次函数;(2)14(3)15;525
18.(1)y=-2x+160;(2)50元,1200元;(3)20件
19.(1)(36-3x)(2)8
(3)当x为米时,苗圃ABCD的最大面积为平方米
20.(1)C(5,3)(2)(3)a≥或a<-1或a=-
同课章节目录
