安徽省马鞍山市九年级上24.2 直线与圆的位置关系练习
文档属性
| 名称 | 安徽省马鞍山市九年级上24.2 直线与圆的位置关系练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 184.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-06 00:00:00 | ||
图片预览


文档简介
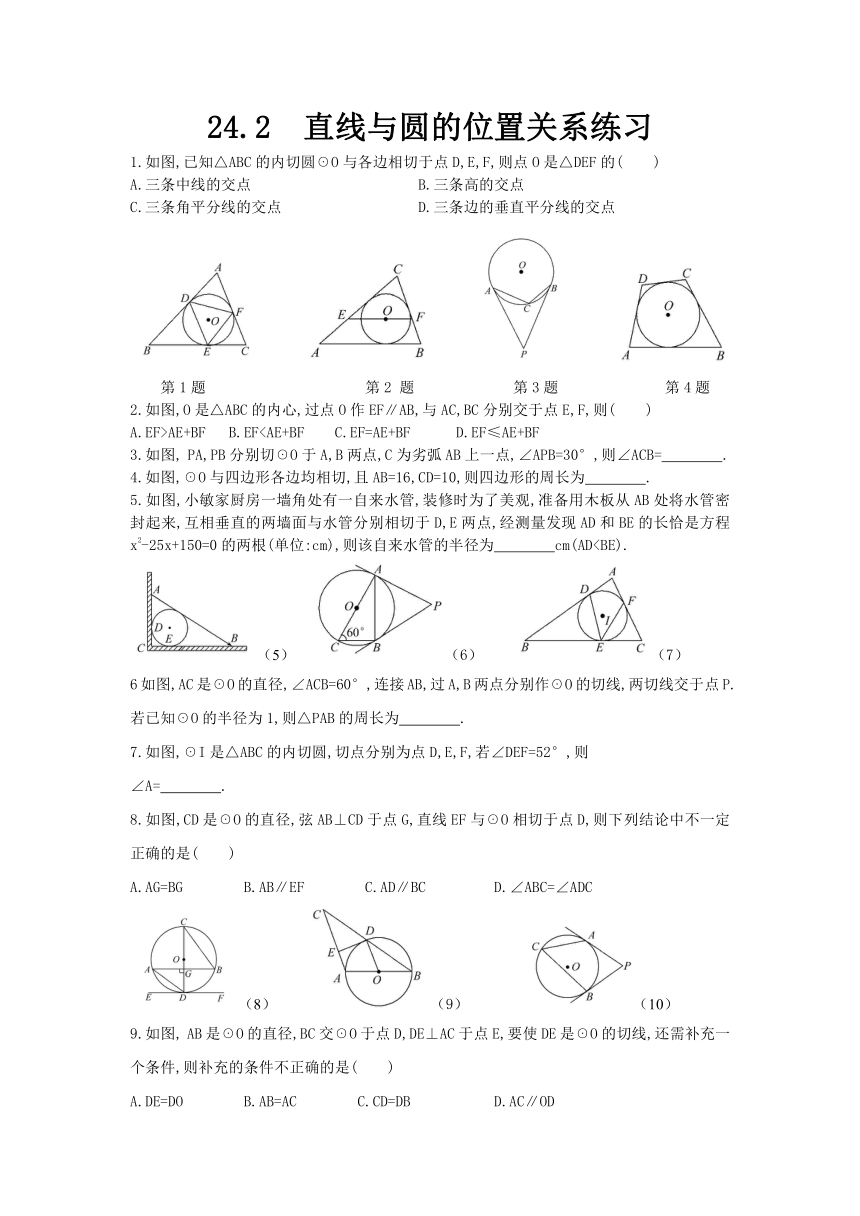
24.2 直线与圆的位置关系练习
1.如图,已知△ABC的内切圆☉O与各边相切于点D,E,F,则点O是△DEF的( )
A.三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三条边的垂直平分线的交点
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题 第2 题 第3题 第4题
2.如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EF3.如图, PA,PB分别切☉O于A,B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB= .
4.如图,☉O与四边形各边均相切,且AB=16,CD=10,则四边形的周长为 .
5.如图,小敏家厨房一墙角处有一自来水管 ( http: / / www.21cnjy.com ),装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量发现AD和BE的长恰是方程x2-25x+150=0的两根(单位:cm),则该自来水管的半径为 cm(AD( http: / / www.21cnjy.com ) (5) ( http: / / www.21cnjy.com )(6) ( http: / / www.21cnjy.com )(7)
6如图,AC是☉O的直径,∠ACB=60° ( http: / / www.21cnjy.com ),连接AB,过A,B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为 .
7.如图,☉I是△ABC的内切圆,切点分别为点D,E,F,若∠DEF=52°,则
∠A= .
8.如图,CD是☉O的直径,弦AB⊥CD于点G,直线EF与☉O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
( http: / / www.21cnjy.com ) (8) ( http: / / www.21cnjy.com ) (9) ( http: / / www.21cnjy.com )(10)
9.如图, AB是☉O的直径,BC交☉O于点D,DE⊥AC于点E,要使DE是☉O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
10.(2013·天津中考)如图,PA,PB分别切☉O于点A,B,若∠P=70°,则∠C的大小为 .
11. (2013·黔西南州中考)如图所示,线段AB是☉O的直径,∠CDB=20°,过点C作☉O的切线交AB的延长线于点E,则∠E等于( )
A.50° B.40° C.60° D.70°
( http: / / www.21cnjy.com ) (11) ( http: / / www.21cnjy.com )(12) ( http: / / www.21cnjy.com )(13)
12.(2013·永州中考)如图,已知△ABC内接于☉O,BC是☉O的直径,MN与☉O相切,切点为A,若∠MAB=30°.则∠B= .
13.如图13,AB是⊙O的直径,DE切⊙O于点C,需使AE⊥DE,须加的一个条件是_____
14.(8分)(2013·湛江中考)如图,已知AB是☉O的直径,P为☉O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为☉O的切线. (2)若OB=5,OP=,求AC的长.
( http: / / www.21cnjy.com )
15.如图,AB为☉O的直径,BC切☉O于B,CO交☉O于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
( http: / / www.21cnjy.com )
16.如图,P是☉O外一点,PA切☉O于点 ( http: / / www.21cnjy.com )A,AB是☉O的直径,BC∥OP且交☉O于点C,请准确判断直线PC与☉O是怎样的位置关系,并说明理由.
( http: / / www.21cnjy.com )
17.(10分)如图,在△ ( http: / / www.21cnjy.com )ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D,若AE=2,AD=4.(1)求☉O的直径BE的长.(2)计算△ABC的面积.
( http: / / www.21cnjy.com )
18. (10分)已知,如图7,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2x-8与y轴交于P.(1)求证:PC是⊙D的切线;(2)判断在直线PC上是否存在点E,使得S△EOC=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
19.已知:如图12,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2,BC=4.
(1) 求以AO、BO两线段长为根的一 ( http: / / www.21cnjy.com )元二次方程; (2) 求图象经过A、B、C三点的二次函数的表达式;(3) 设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
( http: / / www.21cnjy.com )
20.如图,在⊙O中,半径OC与弦 ( http: / / www.21cnjy.com )AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点,若OE=4,OF=6,求⊙O的半径和CD的长。
1.如图,已知△ABC的内切圆☉O与各边相切于点D,E,F,则点O是△DEF的( )
A.三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三条边的垂直平分线的交点
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题 第2 题 第3题 第4题
2.如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EF
4.如图,☉O与四边形各边均相切,且AB=16,CD=10,则四边形的周长为 .
5.如图,小敏家厨房一墙角处有一自来水管 ( http: / / www.21cnjy.com ),装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量发现AD和BE的长恰是方程x2-25x+150=0的两根(单位:cm),则该自来水管的半径为 cm(AD
6如图,AC是☉O的直径,∠ACB=60° ( http: / / www.21cnjy.com ),连接AB,过A,B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为 .
7.如图,☉I是△ABC的内切圆,切点分别为点D,E,F,若∠DEF=52°,则
∠A= .
8.如图,CD是☉O的直径,弦AB⊥CD于点G,直线EF与☉O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
( http: / / www.21cnjy.com ) (8) ( http: / / www.21cnjy.com ) (9) ( http: / / www.21cnjy.com )(10)
9.如图, AB是☉O的直径,BC交☉O于点D,DE⊥AC于点E,要使DE是☉O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
10.(2013·天津中考)如图,PA,PB分别切☉O于点A,B,若∠P=70°,则∠C的大小为 .
11. (2013·黔西南州中考)如图所示,线段AB是☉O的直径,∠CDB=20°,过点C作☉O的切线交AB的延长线于点E,则∠E等于( )
A.50° B.40° C.60° D.70°
( http: / / www.21cnjy.com ) (11) ( http: / / www.21cnjy.com )(12) ( http: / / www.21cnjy.com )(13)
12.(2013·永州中考)如图,已知△ABC内接于☉O,BC是☉O的直径,MN与☉O相切,切点为A,若∠MAB=30°.则∠B= .
13.如图13,AB是⊙O的直径,DE切⊙O于点C,需使AE⊥DE,须加的一个条件是_____
14.(8分)(2013·湛江中考)如图,已知AB是☉O的直径,P为☉O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为☉O的切线. (2)若OB=5,OP=,求AC的长.
( http: / / www.21cnjy.com )
15.如图,AB为☉O的直径,BC切☉O于B,CO交☉O于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
( http: / / www.21cnjy.com )
16.如图,P是☉O外一点,PA切☉O于点 ( http: / / www.21cnjy.com )A,AB是☉O的直径,BC∥OP且交☉O于点C,请准确判断直线PC与☉O是怎样的位置关系,并说明理由.
( http: / / www.21cnjy.com )
17.(10分)如图,在△ ( http: / / www.21cnjy.com )ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D,若AE=2,AD=4.(1)求☉O的直径BE的长.(2)计算△ABC的面积.
( http: / / www.21cnjy.com )
18. (10分)已知,如图7,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2x-8与y轴交于P.(1)求证:PC是⊙D的切线;(2)判断在直线PC上是否存在点E,使得S△EOC=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
19.已知:如图12,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2,BC=4.
(1) 求以AO、BO两线段长为根的一 ( http: / / www.21cnjy.com )元二次方程; (2) 求图象经过A、B、C三点的二次函数的表达式;(3) 设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
( http: / / www.21cnjy.com )
20.如图,在⊙O中,半径OC与弦 ( http: / / www.21cnjy.com )AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点,若OE=4,OF=6,求⊙O的半径和CD的长。
同课章节目录
