人教版九年级数学下册 27.2.1相似三角形的判定(3) 教学课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定(3) 教学课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第二十七章相似
27.2相似三角形
27.2.1相似三角形的判定
第3课时
1.理解三角形相似的判定定理和直角三角形相似的
特殊判定方法.
2.能够运用三角形相似的判定定理和直角三角形相似的特殊
判定方法进行推理论证和计算.
学习目标
1. 三角形相似的判定方法.
2.全等三角形与相似三角形的关系.
复习巩固
上一节课,我们猜测到以下的两个命题,它们是不是
真命题呢
1.两角分别相等的两个三角形相似;
2.斜边和一条直角边成比例的两个直角三角形相似.
这两个命题是否真命题。
新课导入
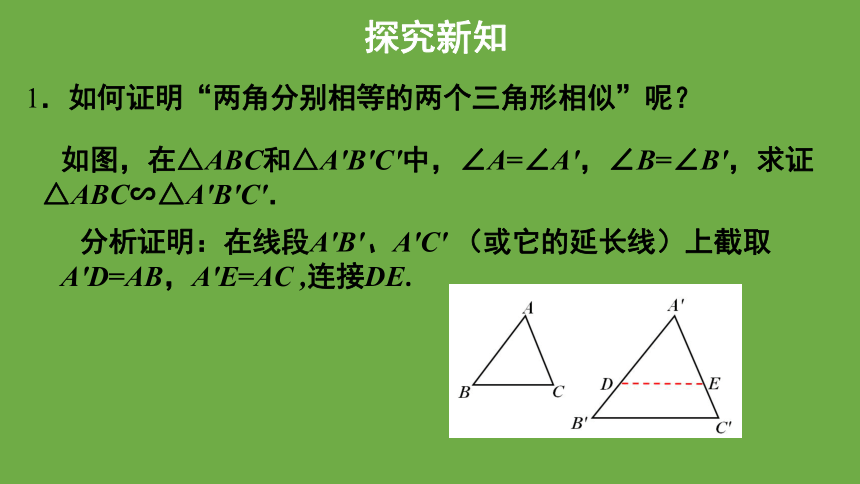
1.如何证明“两角分别相等的两个三角形相似”呢?
如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',求证△ABC∽△A'B'C'.
探究新知
分析证明:在线段A'B'、A'C' (或它的延长线)上截取A'D=AB,A'E=AC ,连接DE.
证明
∴△ABC∽△A'B'C'.
探究新知
:∵∠A=∠A'
∴△A'DE≌△ABC
∴∠A'DE=∠B, ∠A'ED=∠C,DE= BC.
又∵∠B=∠B'
∴∠A'DE=∠B'
∴DE// B'C'
∴△A'DE∽△A'B'C'
∵∠A=∠A',∠B=∠B', ∠C=∠C'
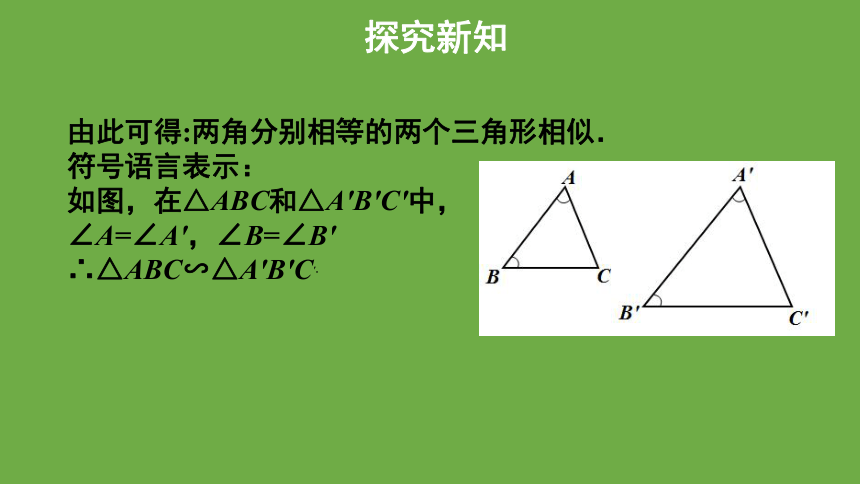
由此可得:两角分别相等的两个三角形相似.
符号语言表示:
如图,在△ABC和△A'B'C'中,
∠A=∠A',∠B=∠B'
∴△ABC∽△A'B'C'.
探究新知
如图,在Rt△ABC和Rt△A‘B’C‘中,∠C=∠C'=90°,
.求证Rt△ABC∽Rt△A'B'C'.
分析:要证Rt△ABC∽Rt△A'B'C',可设法证
,只需证
探究新知
若设
证明:设
,则AB=kA'B, AC=kA'C'.
∴
.
∴Rt△ABC∽Rt△A'B'C'.
由勾股定理得:
探究新知
B
D
A
C
E
F
解:∵∠B=∠C, ∠DFB=∠EFC
∴△DFB∽△EFC(两角分别相等的两个三角形相似)
∵∠B=∠C, ∠A=∠A
∴△ABE∽△ACD(两角分别相等的两个三角形相似)
例1. 如图:∠C=∠B,请指出图中的相似三角形.
例题解析
例2.如图,Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上
一点,AE=5,ED⊥AB,垂足为D.求AD的长.
解:∵ED⊥AB,
∴∠EDA=90°.
又∠C=90°,∠A=∠A,
△AED∽△ABC.
.
∴
例题解析
∴
A
E
C
B
D
例3.如图:AB=3AC,BD=2AE,且BD⊥AD,AE⊥EC,
求证:△ABD∽△CAE
∵AB=2AC,BD=2AE
∴Rt△ABD∽Rt△CAE
例题解析
证明:∵BD⊥AD,AE⊥EC,
∴△ABD和△CAE都是直角三角形.
∴
1.如图,∠ABD=∠C,AD=2,AC=8,求AB的长.
解:∵∠ABD=∠C,∠A=∠A
∴△ABD∽△ACB.
∴
∴
∴AD=4
课堂练习
∴
解:△ACD∽△ABC, △CBD∽△ABC
证明:∵∠ACB=∠ADC=90°,
∠A=∠A,
∴△ACD∽△ABC.
∵∠CDB=∠ACB=90°,
∠B=∠B,
∴△CBD∽△ABC.
课堂练习
2.如图,在Rt△ABC中,CD是斜边上的高,△ACD和△CBD
都和△ABC相似吗?证明你的结论.
(1)已知:在等腰△ABC中,AB=AC,在等腰
△A'B'C'中,A'B'=A'C',且∠B=∠B'.求证△ABC∽△A'B'C'.
∴△ABC∽△A'B'C'.
课堂练习
3.(1)底角相等的两个等腰三角形是否相似?顶角相等的
两个等腰三角形呢?证明你的结论.
证明:∵AB=AC∴∠B=∠C.
∵A'B'=A'C',
∴∠B'=∠C'.
又∠B=∠B',
∴∠C=∠C'.
(2)已知:在等腰△ABC中,AB=AC,在等腰△A'B'C'中,
A'B'=A'C',并且∠A=∠A'.求证△ABC∽△A'B'C'.
证明:∵在△ABC中,AB=AC,∠B=∠C,
∴2∠B=180°-∠A.
.
同理,在△A'B'C'中,A'B'=A'C',∠B'=∠C',
∴2∠B'=180°-∠A'.
又∠A=∠A',
∴∠B=∠B'.
∴△ABC∽△A'B'C'.
课堂练习
∴
三角形相似的判定方法共有几种:
1.通过定义(比较复杂,烦琐);
2.平行于三角形一边的直线和其他两边相交,所构成的
三角形与原三角形相似(只能在特定的图形里面使用);
3.三边对应成比例的两个三角形相似;
4.两边对应成比例且夹角相等的两个三角形相似;
5.两角分别相等的两个三角形相似;
6.两个直角三角形的斜边和一条直角边对应成比例.
课堂小结
再见
第二十七章相似
27.2相似三角形
27.2.1相似三角形的判定
第3课时
1.理解三角形相似的判定定理和直角三角形相似的
特殊判定方法.
2.能够运用三角形相似的判定定理和直角三角形相似的特殊
判定方法进行推理论证和计算.
学习目标
1. 三角形相似的判定方法.
2.全等三角形与相似三角形的关系.
复习巩固
上一节课,我们猜测到以下的两个命题,它们是不是
真命题呢
1.两角分别相等的两个三角形相似;
2.斜边和一条直角边成比例的两个直角三角形相似.
这两个命题是否真命题。
新课导入
1.如何证明“两角分别相等的两个三角形相似”呢?
如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',求证△ABC∽△A'B'C'.
探究新知
分析证明:在线段A'B'、A'C' (或它的延长线)上截取A'D=AB,A'E=AC ,连接DE.
证明
∴△ABC∽△A'B'C'.
探究新知
:∵∠A=∠A'
∴△A'DE≌△ABC
∴∠A'DE=∠B, ∠A'ED=∠C,DE= BC.
又∵∠B=∠B'
∴∠A'DE=∠B'
∴DE// B'C'
∴△A'DE∽△A'B'C'
∵∠A=∠A',∠B=∠B', ∠C=∠C'
由此可得:两角分别相等的两个三角形相似.
符号语言表示:
如图,在△ABC和△A'B'C'中,
∠A=∠A',∠B=∠B'
∴△ABC∽△A'B'C'.
探究新知
如图,在Rt△ABC和Rt△A‘B’C‘中,∠C=∠C'=90°,
.求证Rt△ABC∽Rt△A'B'C'.
分析:要证Rt△ABC∽Rt△A'B'C',可设法证
,只需证
探究新知
若设
证明:设
,则AB=kA'B, AC=kA'C'.
∴
.
∴Rt△ABC∽Rt△A'B'C'.
由勾股定理得:
探究新知
B
D
A
C
E
F
解:∵∠B=∠C, ∠DFB=∠EFC
∴△DFB∽△EFC(两角分别相等的两个三角形相似)
∵∠B=∠C, ∠A=∠A
∴△ABE∽△ACD(两角分别相等的两个三角形相似)
例1. 如图:∠C=∠B,请指出图中的相似三角形.
例题解析
例2.如图,Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上
一点,AE=5,ED⊥AB,垂足为D.求AD的长.
解:∵ED⊥AB,
∴∠EDA=90°.
又∠C=90°,∠A=∠A,
△AED∽△ABC.
.
∴
例题解析
∴
A
E
C
B
D
例3.如图:AB=3AC,BD=2AE,且BD⊥AD,AE⊥EC,
求证:△ABD∽△CAE
∵AB=2AC,BD=2AE
∴Rt△ABD∽Rt△CAE
例题解析
证明:∵BD⊥AD,AE⊥EC,
∴△ABD和△CAE都是直角三角形.
∴
1.如图,∠ABD=∠C,AD=2,AC=8,求AB的长.
解:∵∠ABD=∠C,∠A=∠A
∴△ABD∽△ACB.
∴
∴
∴AD=4
课堂练习
∴
解:△ACD∽△ABC, △CBD∽△ABC
证明:∵∠ACB=∠ADC=90°,
∠A=∠A,
∴△ACD∽△ABC.
∵∠CDB=∠ACB=90°,
∠B=∠B,
∴△CBD∽△ABC.
课堂练习
2.如图,在Rt△ABC中,CD是斜边上的高,△ACD和△CBD
都和△ABC相似吗?证明你的结论.
(1)已知:在等腰△ABC中,AB=AC,在等腰
△A'B'C'中,A'B'=A'C',且∠B=∠B'.求证△ABC∽△A'B'C'.
∴△ABC∽△A'B'C'.
课堂练习
3.(1)底角相等的两个等腰三角形是否相似?顶角相等的
两个等腰三角形呢?证明你的结论.
证明:∵AB=AC∴∠B=∠C.
∵A'B'=A'C',
∴∠B'=∠C'.
又∠B=∠B',
∴∠C=∠C'.
(2)已知:在等腰△ABC中,AB=AC,在等腰△A'B'C'中,
A'B'=A'C',并且∠A=∠A'.求证△ABC∽△A'B'C'.
证明:∵在△ABC中,AB=AC,∠B=∠C,
∴2∠B=180°-∠A.
.
同理,在△A'B'C'中,A'B'=A'C',∠B'=∠C',
∴2∠B'=180°-∠A'.
又∠A=∠A',
∴∠B=∠B'.
∴△ABC∽△A'B'C'.
课堂练习
∴
三角形相似的判定方法共有几种:
1.通过定义(比较复杂,烦琐);
2.平行于三角形一边的直线和其他两边相交,所构成的
三角形与原三角形相似(只能在特定的图形里面使用);
3.三边对应成比例的两个三角形相似;
4.两边对应成比例且夹角相等的两个三角形相似;
5.两角分别相等的两个三角形相似;
6.两个直角三角形的斜边和一条直角边对应成比例.
课堂小结
再见
