人教版九年级数学下册 28.2.1解直角三角形 教学课件(共19张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.2.1解直角三角形 教学课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 485.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 17:38:20 | ||
图片预览




文档简介
(共19张PPT)
第二十八章锐角三角函数
28.2解直角三角形及其应用
28.2.1解直角三角形
1.了解解直角三角形的含义和条件.
2.能根据直角三角形中除直角以外的两个元素
(至少有一个是边)解直角三角形.
学习目标
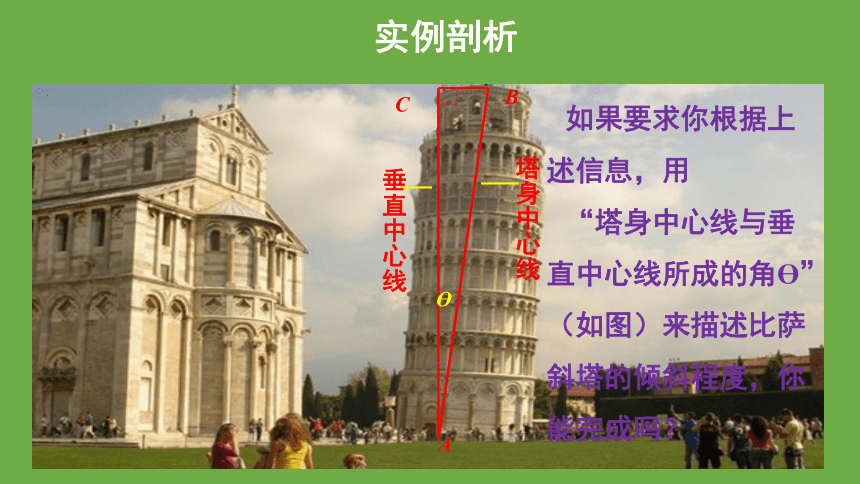
实例剖析
意大利比萨斜塔在1350年落成时就已倾斜,其塔顶中心点偏离垂直中心线2.1 m.1972年比萨地区发生地震,这座高54.5 m的斜塔在大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2 m,而且还以每年增加1 cm的速度继续倾斜,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔进行维修纠偏,2001年竣工,此时塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8 cm.
实例剖析
A
B
C
塔身中心线
垂直中心线
如果要求你根据上述信息,用
“塔身中心线与垂直中心线所成的角 ”(如图)来描述比萨斜塔的倾斜程度,你能完成吗?
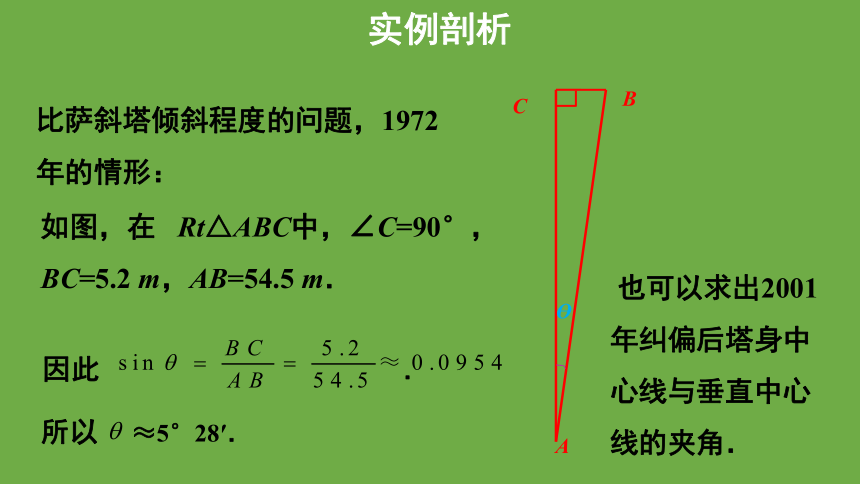
实例剖析
如图,在 Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m.
因此 .
所以 ≈5°28′.
也可以求出2001年纠偏后塔身中心线与垂直中心线的夹角.
A
B
C
比萨斜塔倾斜程度的问题,1972年的情形:
实例剖析
上述实际问题抽象为数学问题,就是已知直角三角形的某些边长,求其锐角的度数.
A
B
C
在Rt △ABC中,你还能求出其他未知的边和角吗?
实例剖析
解直角三角形的概念:
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
梳理总结
回想在刚才的解题过程中,用到了哪些知识?试着梳理一下直角三角形中各个元素之间的关系.
在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
梳理总结
A
B
a
b
c
C
(2)两锐角之间的关系
(3)边角之间的关系
(1)三边之间的关系
在解直角三角形的过程中,一般要用到下面一些关系:
;
(勾股定理)
.
∠A+∠B=90°
.
.
;
;
;
;
梳理总结
解直角三角形有几种情况?
解直角三角形,有下面两种情况 (其中至少有一边) :
(1)已知两条边(一直角边一斜边;两直角边)
(2)已知一条边和一个锐角(一直角边一锐角;一斜边一锐角)
梳理总结
例1. 如图,在Rt△ABC中,∠C=90°, ,
解这个直角三角形.
A
B
C
解:
∵
,
.
∴
,
,
,
例题解析
例2. 如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位).
解:∠A=90°﹣∠B=90°﹣35°=55°.
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
∵
,
.
∴
∵
,
∴
.
例题解析
1.如图,已知正方形ABCD的边长为2,如果将线段BD绕着
点B旋转后,点D落在CB的延长线上的点D′处,
那么tan∠BAD′等于( ).
A. 1 B. C. D.
2.如果一个等腰三角形的底边长为10 cm,周长为36 cm,
那么底角的余弦等于( ).
A. B. C. D.
课堂练习
A
B
3.在矩形ABCD中,DE⊥AC于点E,设∠ADE=
,AB=4,则AD的长为( ).
4.某市在“旧城改造”中计划在一块如图所示的三角形空地上
种植某种草皮以美化环境,已知这种草皮每平方米a元,则购买这种草皮至少要( ).
A.450a元 B.225a元 C.150a元 D.300a元
A.3 B. C. D.
ɑ
B
C
,
课堂练习
5 .在Rt△ABC中,∠C=90°,a = 30 , b = 20,解这个直角三角形.
解:根据勾股定理,得
A
B
C
b=20
a=30
c
∵
,
.
∴
,
.
课堂练习
6 .在Rt△ABC中,∠C=90°,∠B=72°,c = 14,解这个直角三角形.
A
B
C
b
a
c=14
∵
,
∴
.
∵
,
∴
.
解:
.
课堂练习
1.解直角三角形是由直角三角形中已知的元素求出其余未知元素的过程.
2.解直角三角形的条件是除直角外的两个元素,且至少需要一边,即已知两边或已知一边一锐角.
课堂小结
再见
第二十八章锐角三角函数
28.2解直角三角形及其应用
28.2.1解直角三角形
1.了解解直角三角形的含义和条件.
2.能根据直角三角形中除直角以外的两个元素
(至少有一个是边)解直角三角形.
学习目标
实例剖析
意大利比萨斜塔在1350年落成时就已倾斜,其塔顶中心点偏离垂直中心线2.1 m.1972年比萨地区发生地震,这座高54.5 m的斜塔在大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2 m,而且还以每年增加1 cm的速度继续倾斜,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔进行维修纠偏,2001年竣工,此时塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8 cm.
实例剖析
A
B
C
塔身中心线
垂直中心线
如果要求你根据上述信息,用
“塔身中心线与垂直中心线所成的角 ”(如图)来描述比萨斜塔的倾斜程度,你能完成吗?
实例剖析
如图,在 Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m.
因此 .
所以 ≈5°28′.
也可以求出2001年纠偏后塔身中心线与垂直中心线的夹角.
A
B
C
比萨斜塔倾斜程度的问题,1972年的情形:
实例剖析
上述实际问题抽象为数学问题,就是已知直角三角形的某些边长,求其锐角的度数.
A
B
C
在Rt △ABC中,你还能求出其他未知的边和角吗?
实例剖析
解直角三角形的概念:
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
梳理总结
回想在刚才的解题过程中,用到了哪些知识?试着梳理一下直角三角形中各个元素之间的关系.
在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
梳理总结
A
B
a
b
c
C
(2)两锐角之间的关系
(3)边角之间的关系
(1)三边之间的关系
在解直角三角形的过程中,一般要用到下面一些关系:
;
(勾股定理)
.
∠A+∠B=90°
.
.
;
;
;
;
梳理总结
解直角三角形有几种情况?
解直角三角形,有下面两种情况 (其中至少有一边) :
(1)已知两条边(一直角边一斜边;两直角边)
(2)已知一条边和一个锐角(一直角边一锐角;一斜边一锐角)
梳理总结
例1. 如图,在Rt△ABC中,∠C=90°, ,
解这个直角三角形.
A
B
C
解:
∵
,
.
∴
,
,
,
例题解析
例2. 如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位).
解:∠A=90°﹣∠B=90°﹣35°=55°.
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
∵
,
.
∴
∵
,
∴
.
例题解析
1.如图,已知正方形ABCD的边长为2,如果将线段BD绕着
点B旋转后,点D落在CB的延长线上的点D′处,
那么tan∠BAD′等于( ).
A. 1 B. C. D.
2.如果一个等腰三角形的底边长为10 cm,周长为36 cm,
那么底角的余弦等于( ).
A. B. C. D.
课堂练习
A
B
3.在矩形ABCD中,DE⊥AC于点E,设∠ADE=
,AB=4,则AD的长为( ).
4.某市在“旧城改造”中计划在一块如图所示的三角形空地上
种植某种草皮以美化环境,已知这种草皮每平方米a元,则购买这种草皮至少要( ).
A.450a元 B.225a元 C.150a元 D.300a元
A.3 B. C. D.
ɑ
B
C
,
课堂练习
5 .在Rt△ABC中,∠C=90°,a = 30 , b = 20,解这个直角三角形.
解:根据勾股定理,得
A
B
C
b=20
a=30
c
∵
,
.
∴
,
.
课堂练习
6 .在Rt△ABC中,∠C=90°,∠B=72°,c = 14,解这个直角三角形.
A
B
C
b
a
c=14
∵
,
∴
.
∵
,
∴
.
解:
.
课堂练习
1.解直角三角形是由直角三角形中已知的元素求出其余未知元素的过程.
2.解直角三角形的条件是除直角外的两个元素,且至少需要一边,即已知两边或已知一边一锐角.
课堂小结
再见
