人教版九年级数学下册 28.2.2解直角三角形应用举例(2) 教学课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.2.2解直角三角形应用举例(2) 教学课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 17:41:26 | ||
图片预览






文档简介
(共16张PPT)
第二十八章锐角三角函数
28.2解直角三角形及其应用
28.2.2应用举例
第2课时
能利用解直角三角形的知识解决非直角三角形的问题.
学习目标
A
B
a
b
c
C
(2)两锐角之间的关系
(3)边角之间的关系:
(1)三边之间的关系
在解直角三角形的过程中,一般要用到下面一些关系:
;
(勾股定理)
.
∠A+∠B=90°
.
.
;
;
;
;
复习导入
2.用直角三角形的知识解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
复习导入
例1.如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离
灯塔P有多远(cos 25°≈0.906,结果取整数)?
65°
34°
P
B
C
A
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505.
例题解析
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130 n mile .
∵
,
∴
.
65°
34°
P
B
C
A
例题解析
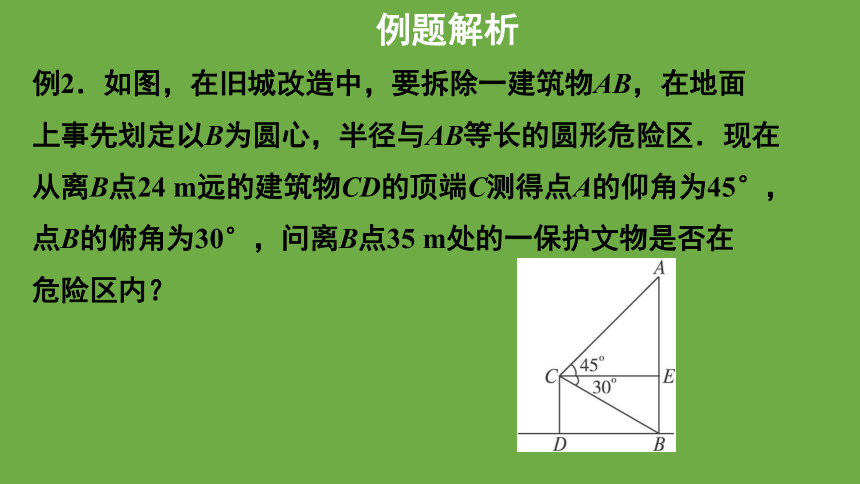
例2.如图,在旧城改造中,要拆除一建筑物AB,在地面
上事先划定以B为圆心,半径与AB等长的圆形危险区.现在
从离B点24 m远的建筑物CD的顶端C测得点A的仰角为45°,
点B的俯角为30°,问离B点35 m处的一保护文物是否在
危险区内?
例题解析
解:在Rt△BEC中,CE=BD=24(m),∠BCE=30°,
∴BE=CE·tan 30°=
.
在Rt△AEC中,∵∠ACE=45°,CE=24,
∴AE=24.
∴AB=24+
≈37.9(m).
∵35<37.9,
∴离B点35 m处的一保护文物在危险区内.
例题解析
例3“村村通公路工程”拉近了城乡距离,加快了我区农村建设步伐,如图所示,C村村民欲修建一条水泥公路,将C村与区级公路相连,在公路A处测得C村在北偏东60°方向,前进500m,在B处测得C村在北偏东30°方向,为节约资源,要求所修公路的长度最短,画出符合条件的公路示意图,
并求出公路长度.(结果保留整数)
30°
C
A
60°
B
区级公路
D
∟
例题解析
解:
∴AD=
在Rt△CBD中,根据题意得
∠CBD=60°.
∵tan∠CBD=
∴BD=
∴
解得CD=433
答:公路的长度约为433m.
例题解析
在Rt△ACD中,根据题意得∠CAD=30°.
过点C作CD⊥AB,垂足落在AB的延长线上,CD即所修公路,CD的长度即为公路长度.
∵tan∠CAD=
又∵AD﹣BD=500
1.如图,海中有一个小岛A,它周围8 n mile内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12 n mile到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
课堂练习
设DF=x,AD=2x,
则在Rt △ ADF中,根据勾股定理得
>8.
因此,没有触礁的危险.
.
∴在Rt △ABF中,
由
得
∴
B
A
D
F
∟
课堂练习
解:由点A作BD的垂线交BD的延长线于点F,垂足为F,
∠AFD=90°.由题意图示可知∠DAF=30 °
2. 如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1∶ 1.5是指坡面的铅直高度AF与水平宽度BF的比,
斜面坡度i=1∶ 3是指DE与CE的比.根据图中数据,求:
(1)坡角α和β的度数;
(2)斜坡AB的长(结果保留小数点后一位).
B
A
D
F
E
C
6 m
α
β
i=1∶3
i=1∶1.5
课堂练习
∵
,
在Rt △CDE中,∠CED=90°,
,
(2)在Rt △AFB中,∠AFB=90°,
由sin α=sin33°41′24″= , AF=6可求出AB≈10.8 m.
B
A
D
F
E
C
6 m
α
β
i=1∶3
i=1∶1.5
课堂练习
∴α=33°41′24″;
∴β=18°26′6″.
2.解:(1)在Rt △AFB中,∠AFB=90°,
∵
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等
去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
再见
第二十八章锐角三角函数
28.2解直角三角形及其应用
28.2.2应用举例
第2课时
能利用解直角三角形的知识解决非直角三角形的问题.
学习目标
A
B
a
b
c
C
(2)两锐角之间的关系
(3)边角之间的关系:
(1)三边之间的关系
在解直角三角形的过程中,一般要用到下面一些关系:
;
(勾股定理)
.
∠A+∠B=90°
.
.
;
;
;
;
复习导入
2.用直角三角形的知识解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
复习导入
例1.如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离
灯塔P有多远(cos 25°≈0.906,结果取整数)?
65°
34°
P
B
C
A
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505.
例题解析
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130 n mile .
∵
,
∴
.
65°
34°
P
B
C
A
例题解析
例2.如图,在旧城改造中,要拆除一建筑物AB,在地面
上事先划定以B为圆心,半径与AB等长的圆形危险区.现在
从离B点24 m远的建筑物CD的顶端C测得点A的仰角为45°,
点B的俯角为30°,问离B点35 m处的一保护文物是否在
危险区内?
例题解析
解:在Rt△BEC中,CE=BD=24(m),∠BCE=30°,
∴BE=CE·tan 30°=
.
在Rt△AEC中,∵∠ACE=45°,CE=24,
∴AE=24.
∴AB=24+
≈37.9(m).
∵35<37.9,
∴离B点35 m处的一保护文物在危险区内.
例题解析
例3“村村通公路工程”拉近了城乡距离,加快了我区农村建设步伐,如图所示,C村村民欲修建一条水泥公路,将C村与区级公路相连,在公路A处测得C村在北偏东60°方向,前进500m,在B处测得C村在北偏东30°方向,为节约资源,要求所修公路的长度最短,画出符合条件的公路示意图,
并求出公路长度.(结果保留整数)
30°
C
A
60°
B
区级公路
D
∟
例题解析
解:
∴AD=
在Rt△CBD中,根据题意得
∠CBD=60°.
∵tan∠CBD=
∴BD=
∴
解得CD=433
答:公路的长度约为433m.
例题解析
在Rt△ACD中,根据题意得∠CAD=30°.
过点C作CD⊥AB,垂足落在AB的延长线上,CD即所修公路,CD的长度即为公路长度.
∵tan∠CAD=
又∵AD﹣BD=500
1.如图,海中有一个小岛A,它周围8 n mile内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12 n mile到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
课堂练习
设DF=x,AD=2x,
则在Rt △ ADF中,根据勾股定理得
>8.
因此,没有触礁的危险.
.
∴在Rt △ABF中,
由
得
∴
B
A
D
F
∟
课堂练习
解:由点A作BD的垂线交BD的延长线于点F,垂足为F,
∠AFD=90°.由题意图示可知∠DAF=30 °
2. 如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1∶ 1.5是指坡面的铅直高度AF与水平宽度BF的比,
斜面坡度i=1∶ 3是指DE与CE的比.根据图中数据,求:
(1)坡角α和β的度数;
(2)斜坡AB的长(结果保留小数点后一位).
B
A
D
F
E
C
6 m
α
β
i=1∶3
i=1∶1.5
课堂练习
∵
,
在Rt △CDE中,∠CED=90°,
,
(2)在Rt △AFB中,∠AFB=90°,
由sin α=sin33°41′24″= , AF=6可求出AB≈10.8 m.
B
A
D
F
E
C
6 m
α
β
i=1∶3
i=1∶1.5
课堂练习
∴α=33°41′24″;
∴β=18°26′6″.
2.解:(1)在Rt △AFB中,∠AFB=90°,
∵
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等
去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
再见
