沪科版初中物理八年级10.1科学探究:杠杆的平衡条件 同步习题(含解析)
文档属性
| 名称 | 沪科版初中物理八年级10.1科学探究:杠杆的平衡条件 同步习题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 554.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-24 21:10:58 | ||
图片预览




文档简介
10.1 科学探究:杠杆的平衡条件
知识梳理
定义:将一根在力的作用下可绕 转动的硬棒叫杠杆
杠杆的五要素: 、 、 、 、
杠杆 杠杆的平衡条件:
省力杠杆:L1 L2,F1 F2;省力但 ;例如
杠杆分类 费力杠杆:L1 L2,F1 F2;费力但 ;例如
等臂杠杆:L1 L2,F1 F2;不省力也 ;例如
基础知识
1.关于杠杆,下列说法正确的是( )
A.力臂一定是杠杆上的一部分
B.力臂就是从支点到力的作用线的距离
C.只有在费力情况时才能省功
D.杠杆平衡时,动力+动力臂与阻力+阻力臂总是相等的
2.如图所示的杠杆中,所画F力臂正确的是( )
A. B.
C. D.
3.如图所示,杠杆处于平衡状态,且杠杆上的刻度均匀,各钩码质量相等。如果把杠杆两侧的钩码各取下一个,保持钩码位置不变,则杠杆会( )
A.左端下沉 B.右端下沉 C.仍然平衡 D.无法判断
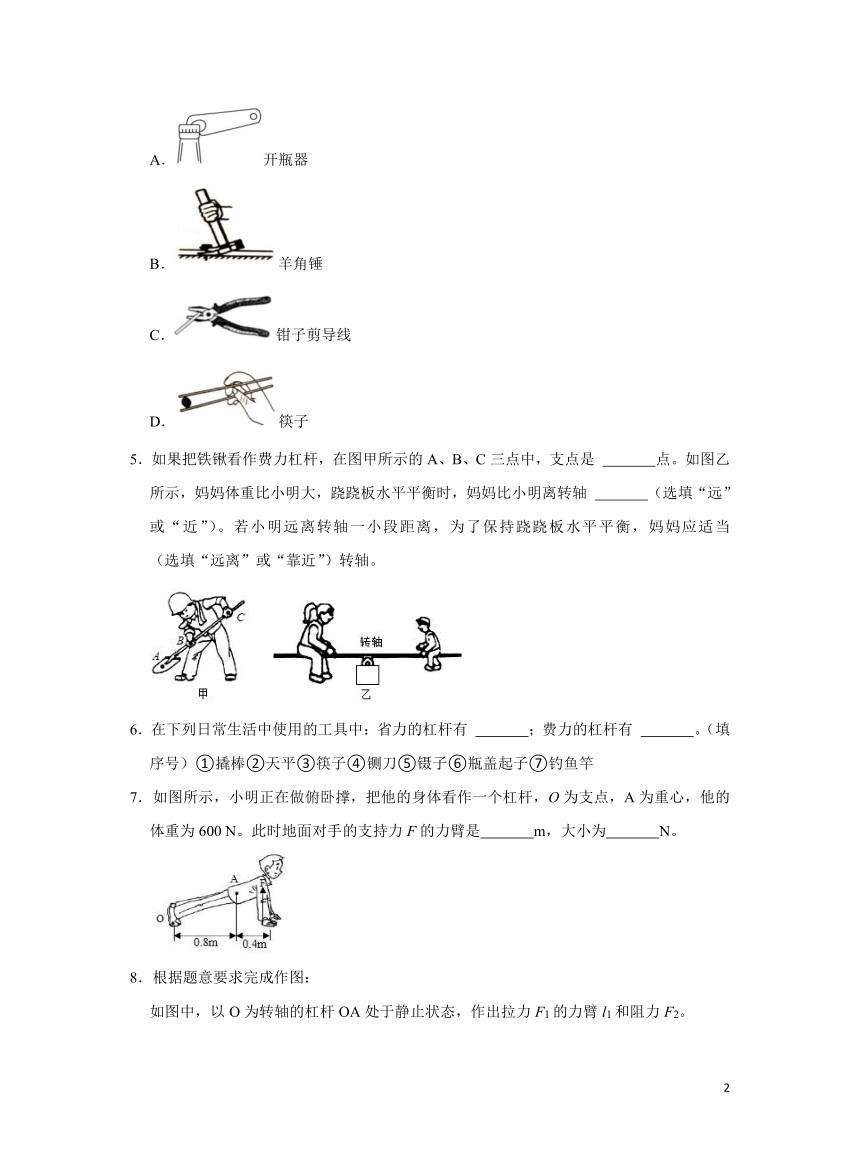
4.下列各图所示的工具,正常使用时省距离的是( )
A.开瓶器
B.羊角锤
C.钳子剪导线
D.筷子
5.如果把铁锹看作费力杠杆,在图甲所示的A、B、C三点中,支点是 点。如图乙所示,妈妈体重比小明大,跷跷板水平平衡时,妈妈比小明离转轴 (选填“远”或“近”)。若小明远离转轴一小段距离,为了保持跷跷板水平平衡,妈妈应适当 (选填“远离”或“靠近”)转轴。
6.在下列日常生活中使用的工具中:省力的杠杆有 ;费力的杠杆有 。(填序号)①撬棒②天平③筷子④铡刀⑤镊子⑥瓶盖起子⑦钓鱼竿
7.如图所示,小明正在做俯卧撑,把他的身体看作一个杠杆,O为支点,A为重心,他的体重为600 N。此时地面对手的支持力F的力臂是 m,大小为 N。
8.根据题意要求完成作图:
如图中,以O为转轴的杠杆OA处于静止状态,作出拉力F1的力臂l1和阻力F2。
重难点突破
9.如图所示的工具中,在使用时与其它三种不是同一种类型的是( )
A.取碗夹子 B.核桃夹子
C.羊角锤 D.修枝剪刀
10.如图所示,小华用苹果和桔子来玩跷跷板,她将苹果、桔子分别挂在轻杆的左、右两端,放手后,杆马上转动起来。使杆逆时针转动的力是( )
A.苹果的重力 B.桔子的重力
C.苹果对杆的拉力 D.杆对桔子的拉力
11.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面。则( )
A.F甲>F乙,因为甲方法的动力臂长
B.F甲<F乙,因为乙方法的阻力臂长
C.F甲>F乙,因为乙方法时阻力臂短
D.F甲=F乙
12.如图所示是自卸车的示意图,车厢部分可视为杠杆,则下列分析正确的是( )
A.B是支点,液压杆施加的力是动力,货物重力是阻力
B.B是支点,货物A放在车厢前部可省力
C.C是支点,货物A放在车厢前部可省力
D.C是支点,货物A放在车厢后部可省力
13.如图所示,轻质杠杆OA可绕O点转动,通过定滑轮用力拉动杠杆缓慢转动,在图示位置时,杠杆的动力臂力L作图正确的是( )
A.
B.
C.
D.
14.如图所示,绕固定点O转动的轻质杠杆,中点处挂一重物G,端点处有一个始终垂直于杠杆的拉力F,使其缓慢地向图中A位置移动到B的过程中,关于拉力F的说法正确的是( )
A.一直增大 B.先变大后变小
C.先变小后变大 D.保持不变
15.超市里的手推车如图所示,某顾客推着空车前进时,当前轮遇障碍物A时,顾客向下按扶把,这时手推车可看成杠杆,支点是 点;当后轮遇到障碍物A时,顾客向上提扶把,这时支点是 点。
16.停车场入口处常用横杆来控制车辆的进出,如图甲所示。我们可以把该装置简化成如图乙所示的杠杆,若横杆AB粗细相同,质量分布均匀,重120 N,AB=2.8 m,AO=0.3 m。要使横杆AB保持水平平衡,则在A端施加最小动力的方向是竖直向 ,这个力的大小是 N,此杠杆是一个 杠杆(选填“省力”、“费力”或“等臂”)。
17.如图所示,在杠杆AOB的A端挂一重物G,要使杠杆在如图所示的位置平衡,请画出在杠杆上施加的最小动力F1及阻力F2的示意图。
18.如图,杠杆在水平位置保持静止,L1为动力F1的力臂,请在图中作出动力F1及阻力臂L2的示意图。
19.如图所示是探究“杠杆平衡的条件”的实验,实验所用的杠杆刻度和质量分布均匀,每个钩码相同。
(1)实验时,先把杠杆放在水平桌面上(如图甲所示),此时应将杠杆左、右两端的平衡螺母向 (选填“左”或“右”)移,直至杠杆在水平位置平衡。
(2)杠杆调节平衡后,在杠杆A处挂两个钩码(如图乙所示),要使杠杆重新平衡,此时应在B处挂 个钩码。
(3)若用弹簧测力计在C处沿竖直方向向上拉杠杆(如图丙所示),使杠杆在水平位置重新平衡,此时弹簧测力计的示数为 N;若将弹簧测力计逐渐向左斜拉(如图丁所示),使杠杆在水平位置仍然平衡,则拉力的力臂将 (选填“变大”、“不变”或“变小”)。杠杆平衡后,在整个实验过程中, (选填“可以”或“不可以”)再调节杠杆两端的平衡螺母。
(4)在实验中,多次改变力和力臂的大小主要是为了
A.减小摩擦
B.使实验数据更准确
C.多次测量求平均值可以减小误差
D.获取多组实验数据归纳出物理规律
能力提升
20.如图所示,用一根自重可忽略不计的撬棒撬石块,若撬棒C点受到石块的压力是1500 N,且AB=1 m,AD=0.5 m,CD=0.3 m,则要撬动该石块所用的最小的力是( )
A.900 N B.750 N C.300 N D.150 N
21.看漫画图,小猴和小兔在分萝卜,他们用一个三角形支点支起萝卜,当萝卜平衡时,小兔选择了长的那段萝卜,小猴选择了短的那段,请你分析一下小猴和小兔谁分的萝卜重?( )
A.小兔 B.小猴 C.一样重 D.无法判断
22.一个重为400 N的物体Q,底面积300 cm2,将其放在水平地面上,如图所示,现将物体Q挂在杠杆的B端,在A端悬挂一个重为200 N的物体P,使杠杆在水平位置平衡,忽略杠杆自重的影响,若OA:OB=1:2,那么( )
A.绳子对物体Q的拉力为150 N
B.地面对物体Q的支持力为200 N
C.绳子对物体P的拉力为250 N
D.物体Q对地面的压强是1×104 Pa
23.如图所示,将体积相同的甲、乙两球分别挂在轻质杠杆的AB两端,杠杆处于平衡状态,已知OB>OA;现将两球同时浸没在水中,下列说法正确的是( )
A.杠杆不能平衡,A端下沉
B.杠杆不能平衡,B端下沉
C.由于两球所受浮力大小相等,杠杆仍然不能平衡,B端下沉
D.两球质量未知,无法确定杠杆的平衡状态
24.如图是单塔双索斜拉大桥,索塔两侧对称的拉索承受了桥梁的重力,现仅有一辆载重汽车从桥梁左端速匀速驶向索塔的过程中,左侧拉索拉力大小( )
A.一直减小 B.一直增大
C.先减小后增大 D.保持不变
25.如图所示,有一根均匀铁棒,长为L,OA=,重力G=900 N,为了不使这根铁棒的B端下沉,所需外力F至少应为 N,若F的方向不变,微微抬起这根铁棒的B端,所需外力F′应为 N。
26.甲、乙两个身高相同的人抬着一个木箱沿斜坡上山,木箱的悬点恰好在抬杠的中央,如图1所示,则甲、乙两人所用的力F甲 F乙;如图2所示,甲、乙两人将一木箱从一楼抬上三楼,则甲、乙两人所用的力F甲 F乙(都选填大于、等于或小于)。
参考答案与试题解析
知识梳理
固定点;支点;动力;动力臂;阻力;阻力臂;F1L1=F2L2;>;<;费距离;独轮车、铡刀等;<;>;省距离;镊子、筷子等;=;=;不省距离;天平、定滑轮等。
基础知识
1.【解答】解:A.力臂不一定是杠杆的长度,力臂可能在杠杆上也可能不在杠杆上,故A错误;
B.力臂是从支点到力的作用线的距离,简单地说,就是“点到线”的距离,故B正确;
C.使用任何机械都不能省功,故C错误;
D.根据杠杆的平衡条件,杠杆平衡时,动力×动力臂与阻力×阻力臂总是相等的,故D错误。
故选:B。
2.【解答】解:
AB.因为动力的力臂的做法是过支点作动力作用线的垂线段,而A B选项中线段与动力作用线不垂直,故A.B都错;
C.图中,表示力臂的不是支点到动力作用线的垂线段,故C错;
D.图中表示的是支点到动力作用线的垂线段,故D正确。
故选:D。
3.【解答】解:设一个钩码重为G,杠杆一个小格是L,若将杠杆两侧所挂的钩码各取下一个,则左侧力与力臂的乘积为:1G×4L=4GL,右侧力与力臂的乘积为:3G×2L=6GL,因为4GL<6GL,根据杠杆平衡条件可知,杠杆不能平衡,且右端下沉,故B正确。
故选:B。
4.【解答】解:ABC.开瓶器、羊角锤、钳子在使用时,动力臂大于阻力臂,属于省力杠杆,省力费距离,故ABC错误;
D.筷子在使用时,动力臂小于阻力臂,属于费力杠杆,费力省距离,故D正确。
故选:D。
5.【解答】解:(1)把铁锨看作费力杠杆,杠杆是绕着C点转动,所以C点即为费力杠杆的支点;
(2)跷跷板在水平位置平衡时,设小明的重力为G1,力臂为L1,妈妈的重力为G2,力臂为L2,
因为G1L1=G2L2、G1<G2,所以L1>L2,即妈妈比小明离转轴近;
若小明远离转轴一小段距离,即力臂为L1变大,为了保持跷跷板水平平衡,由G1L1=G2L2知,在G1和G2不变时,L1变大,L2也变大,妈妈应适当远离转轴。
故答案为:C;近;远。
6.【解答】解:
①撬棒在使用过程中,动力臂大于阻力臂,是省力杠杆;
②天平在使用过程中,动力臂等于阻力臂,是等臂杠杆
③筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;
④铡刀在使用过程中,动力臂大于阻力臂,是省力杠杆;
⑤镊子在使用过程中,动力臂小于阻力臂,是费力杠杆;
⑥瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;
⑦钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;
所以省力的杠杆有①④⑥;费力的杠杆有③⑤⑦。
故答案为:①④⑥;③⑤⑦。
7.【解答】解:由图示可知,O为支点,地面对手的支持力的力臂:
L=0.4 m+0.8 m=1.2 m;
由杠杆平衡条件得:FL=GLG,即:F×1.2 m =600 N×0.8 m,
解得:F=400 N。
故答案为:1.2;400。
8.【解答】解:如图所示,O为支点,延长拉力F1的作用线,从点O到F1的作用线作垂线,即为F1的力臂l1;由题可知,重物对杠杆的拉力为阻力F2,方向为竖直向下;如下图所示:
9.【解答】解:取碗夹子在使用过程中,动力臂小于阻力臂,是费力杠杆;核桃夹子、羊角锤、修枝剪刀在使用过程中,动力臂大于阻力臂,是省力杠杆;故A与其他三个不同。
故选:A。
10.【解答】解:苹果和桔子对杠杆的拉力分别为动力和阻力,由图知,动力臂小于阻力臂,根据杠杆平衡条件知,动力大于阻力,因此使杠杆逆时针转动的力是杠杆左端苹果对杆的拉力。
故选:C。
11.【解答】解:两次抬起水泥板时,动力克服的都是水泥板的重力,对于形状规则质地均匀的物体,其重心都在其几何中心上,所以阻力臂都等于动力臂的二分之一,即动力臂都是阻力臂的2倍。
根据杠杆的平衡条件可得:F==G,所以前后两次所用的力相同,故ABC错误,D正确。
故选:D。
12.【解答】解:由图可知车厢绕着点C转动,所以C点为支点;
当物体A放在车厢的后部时,动力臂大于阻力臂,因此省力,所以选项A、B、C都不正确。
故选:D。
13.【解答】解:由题知,杠杆的支点在O处,绳的拉力沿绳方向画,从支点向力的作用线引垂线,如图所示:
故选:C。
14.【解答】解:
由图可知,O为支点,阻力为物体的重力G,由于F始终垂直于杠杆,所以动力臂不变;将杠杆缓慢地由最初位置拉到水平位置时,动力臂不变,阻力不变,阻力臂变大,根据杠杆平衡条件F1L1=F2L2可知,动力变大;
将杠杆从水平位置拉到最终位置时,动力臂不变,阻力不变,阻力臂变小,根据杠杆平衡条件F1L1=F2L2可知,动力变小;所以,在整个过程中,F先变大后变小。
故选:B。
15.【解答】解:支点是杠杆绕着转动的固定点,由图可知,当前轮遇障碍物A时,顾客向下按扶把,这时手推车可绕C点转动,故支点是C点;
当后轮遇到障碍物A时,顾客向上提把,这时手推车可绕B点转动,故支点是B点。
故答案为:C;B。
16.【解答】解:(1)要使横杆AB保持水平平衡,则在A端施加最小力的方向应该竖直向下的;
横杆AB粗细相同、质量分布均匀,所以其重心C在几何中心上,支点为O,则OA就是动力臂,OC就是阻力臂,如下图所示:
已知AB=2.8 m,AO=0.3 m,则阻力臂OC=AB﹣OA=×2.8 m﹣0.3 m=1.1 m,
由杠杆的平衡条件可得:F×OA=G×OC,
则F===440 N。
(3)由题意可知,动力臂AO小于阻力臂OC,为费力杠杆。
故答案为:下;440;费力。
17.【解答】解:杠杆在图示位置平衡,阻力G与阻力臂OA一定,由杠杆平衡条件可知,在阻力与阻力臂一定时,动力臂越大,动力越小,由图示可知,OB为最大动力臂,此时动力最小,过B点作垂直于OB向下的动力F1即可;
重物对杠杆的拉力即为阻力,过A点作竖直向下的力即为阻力F2,如图所示:
18.【解答】解:过L1的上端作力臂L1的垂线即力F1的作用线,与杠杆的交点就是动力的作用点,动力和阻力使杠杆转动的效果相反,则动力F1的方向向上;
由图可知,O为支点,物体对杠杆的拉力是阻力F2,由O向力F2的作用线引垂线,支点到垂足的距离就是力臂L2。如下图所示:
19.【解答】解:(1)因为图甲中杠杆的右端下倾,所以应将两侧的平衡螺母向左移动,使杠杆在水平位置平衡;
(2)设杠杆每一个小格为L,每个钩码的重力为G,
根据杠杆平衡条件F1L1=F2L2得,2G×2L=nG×4L,所以n=1,所以在B处挂1个钩码;
(3)由图丙可知,弹簧测力计的分度值为0.1 N,所以此时弹簧测力计的示数为1.9 N;
当弹簧测力计倾斜拉杠杆时,拉力的力臂小于OC,拉力的力臂变小;
实验过程中,螺母再调节会改变杠杆重心的位置,使杠杆重力对杠杆平衡又产生影响,因此不能再调节平衡螺母;
(4)探究杠杆平衡的条件时,多次改变力和力臂的大小主要是为了获取多组实验数据,排除偶然性,得到普遍规律;故ABC错误,D正确。
故答案为:(1)左;(2)1;(3)1.9;变小;不可以;(4)D。
20.【解答】解:
①若以D点为支点,则作用在A点的最小力应垂直于杠杆斜向下,此时AD为动力臂,CD为阻力臂,如图:
②若以B点为支点,则作用在A点的最小力应垂直于杠杆斜向上,此时AB为动力臂,BC为阻力臂,如图:
由图知,AD<AB,CD>BC,所以②更省力;
如上图,以B为支点,动力臂AB=1 m,阻力臂BC=AB﹣AD﹣CD=1 m﹣0.5 m﹣0.3 m=0.2 m,
由杠杆的平衡条件得:F1×AB=F2×BC,
即:F1×1 m=1500 N×0.2 m,
解得F1=300 N,故C正确。
故选:C。
21.【解答】解:萝卜处于平衡状态,如图所示:
右侧部分重心离支点O较远,故力臂OB较大,左侧部分重心离支点O较近,故力臂OA较小;
根据杠杆平衡条件G1×OA=G2×OB,因为OB>OA,所以G1>G2,
所以小兔选择的那段长萝卜的重力比另一段小些,故B正确。
故选:B。
22.【解答】解:在A端悬挂一个重为200 N的物体P,P处于静止状态,则绳子对物体P的拉力为200 N,故C错误;
杠杆水平位置平衡,由杠杆平衡条件可得:GP OA=FB OB,
杠杆B点受到的拉力:FB=GP=×200 N=100 N,
因相互作用力大小相等,所以,绳子对物体Q的拉力F拉=FB=100 N,故A错误;
因物体Q受到竖直向上绳子的拉力和地面的支持力、竖直向下重力的作用下处于平衡状态,
所以,由力的平衡条件可得:F支持=GQ﹣F拉=400 N﹣100 N=300 N,故B错误;
因地面对Q的支持力和物体Q对地面的压力是一对相互作用力,
所以,物体Q对地面的压力:F压=F支持=300 N,
物体Q对地面的压强:p===1×104 Pa,故D正确。
故选:D。
23.【解答】解:物体没有浸入水中时,根据杠杆平衡条件有G甲×OA=G乙×OB,由图可见OA<OB,则G甲>G乙。物体浸入水中时,对杠杆的拉力F=G﹣F浮,因为两个物体的体积相等,都同时浸没在水中,所以它们受到的浮力相等,即F浮甲=F浮乙;
杠杆A端:(G甲﹣F浮甲)×OA=G甲×OA﹣F浮甲×OA,
杠杆B端:(G乙﹣F浮乙)×OB=G乙×OB﹣F浮乙×OB,
因OA<OB,则F浮甲×OA<F浮乙×OB;又G甲×OA=G乙×OB,
则(G甲×OA﹣F浮甲×OA)>(G乙×OB﹣F浮乙×OB),
因此杠杆的左(A)端下降。
故选:A。
24.【解答】解:以索塔与桥面的交点为支点,左侧拉索的拉力为动力,汽车对桥的压力为阻力,当载重汽车从桥梁左端匀速驶向索塔的过程中,阻力臂逐渐减小,在阻力和动力臂不变时,根据杠杆的平衡条件知左侧拉索拉力大小一直减小,故A正确。
故选:A。
25.【解答】解:
(1)为了不使这根铁棒的B端下沉,此时杠杆的支点是A,动力臂为AB=L+L=L,阻力臂为AO=L,
根据杠杆的平衡条件可得:F×L=G L,所以F=G=×900 N=400 N;
(2)微微抬起这根铁棒的B端,此时支点是C,动力臂为CB=L,阻力臂为CO=L,
根据杠杆的平衡条件可得:F′ L=G×;所以F′===450 N;
故答案为:400;450。
26.【解答】解:(1)如图所示:
LAE为阻力臂,LAF为动力臂;因为:F乙LAF=GLAE,所以:F乙==G,
同理,可求F甲=G,则甲、乙两人所用的力F甲=F乙;
(2)为了方便分析,以木箱的重心为支点(也可以以任何一个人的手为支点),两人施加的力都是竖直向上的,力和力臂的情况如下图所示:
由图可知,L甲<L乙,根据杠杆平衡条件可得:F甲L甲=F乙L乙,
所以可知F甲>F乙。
故答案为:等于;大于。
1
知识梳理
定义:将一根在力的作用下可绕 转动的硬棒叫杠杆
杠杆的五要素: 、 、 、 、
杠杆 杠杆的平衡条件:
省力杠杆:L1 L2,F1 F2;省力但 ;例如
杠杆分类 费力杠杆:L1 L2,F1 F2;费力但 ;例如
等臂杠杆:L1 L2,F1 F2;不省力也 ;例如
基础知识
1.关于杠杆,下列说法正确的是( )
A.力臂一定是杠杆上的一部分
B.力臂就是从支点到力的作用线的距离
C.只有在费力情况时才能省功
D.杠杆平衡时,动力+动力臂与阻力+阻力臂总是相等的
2.如图所示的杠杆中,所画F力臂正确的是( )
A. B.
C. D.
3.如图所示,杠杆处于平衡状态,且杠杆上的刻度均匀,各钩码质量相等。如果把杠杆两侧的钩码各取下一个,保持钩码位置不变,则杠杆会( )
A.左端下沉 B.右端下沉 C.仍然平衡 D.无法判断
4.下列各图所示的工具,正常使用时省距离的是( )
A.开瓶器
B.羊角锤
C.钳子剪导线
D.筷子
5.如果把铁锹看作费力杠杆,在图甲所示的A、B、C三点中,支点是 点。如图乙所示,妈妈体重比小明大,跷跷板水平平衡时,妈妈比小明离转轴 (选填“远”或“近”)。若小明远离转轴一小段距离,为了保持跷跷板水平平衡,妈妈应适当 (选填“远离”或“靠近”)转轴。
6.在下列日常生活中使用的工具中:省力的杠杆有 ;费力的杠杆有 。(填序号)①撬棒②天平③筷子④铡刀⑤镊子⑥瓶盖起子⑦钓鱼竿
7.如图所示,小明正在做俯卧撑,把他的身体看作一个杠杆,O为支点,A为重心,他的体重为600 N。此时地面对手的支持力F的力臂是 m,大小为 N。
8.根据题意要求完成作图:
如图中,以O为转轴的杠杆OA处于静止状态,作出拉力F1的力臂l1和阻力F2。
重难点突破
9.如图所示的工具中,在使用时与其它三种不是同一种类型的是( )
A.取碗夹子 B.核桃夹子
C.羊角锤 D.修枝剪刀
10.如图所示,小华用苹果和桔子来玩跷跷板,她将苹果、桔子分别挂在轻杆的左、右两端,放手后,杆马上转动起来。使杆逆时针转动的力是( )
A.苹果的重力 B.桔子的重力
C.苹果对杆的拉力 D.杆对桔子的拉力
11.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面。则( )
A.F甲>F乙,因为甲方法的动力臂长
B.F甲<F乙,因为乙方法的阻力臂长
C.F甲>F乙,因为乙方法时阻力臂短
D.F甲=F乙
12.如图所示是自卸车的示意图,车厢部分可视为杠杆,则下列分析正确的是( )
A.B是支点,液压杆施加的力是动力,货物重力是阻力
B.B是支点,货物A放在车厢前部可省力
C.C是支点,货物A放在车厢前部可省力
D.C是支点,货物A放在车厢后部可省力
13.如图所示,轻质杠杆OA可绕O点转动,通过定滑轮用力拉动杠杆缓慢转动,在图示位置时,杠杆的动力臂力L作图正确的是( )
A.
B.
C.
D.
14.如图所示,绕固定点O转动的轻质杠杆,中点处挂一重物G,端点处有一个始终垂直于杠杆的拉力F,使其缓慢地向图中A位置移动到B的过程中,关于拉力F的说法正确的是( )
A.一直增大 B.先变大后变小
C.先变小后变大 D.保持不变
15.超市里的手推车如图所示,某顾客推着空车前进时,当前轮遇障碍物A时,顾客向下按扶把,这时手推车可看成杠杆,支点是 点;当后轮遇到障碍物A时,顾客向上提扶把,这时支点是 点。
16.停车场入口处常用横杆来控制车辆的进出,如图甲所示。我们可以把该装置简化成如图乙所示的杠杆,若横杆AB粗细相同,质量分布均匀,重120 N,AB=2.8 m,AO=0.3 m。要使横杆AB保持水平平衡,则在A端施加最小动力的方向是竖直向 ,这个力的大小是 N,此杠杆是一个 杠杆(选填“省力”、“费力”或“等臂”)。
17.如图所示,在杠杆AOB的A端挂一重物G,要使杠杆在如图所示的位置平衡,请画出在杠杆上施加的最小动力F1及阻力F2的示意图。
18.如图,杠杆在水平位置保持静止,L1为动力F1的力臂,请在图中作出动力F1及阻力臂L2的示意图。
19.如图所示是探究“杠杆平衡的条件”的实验,实验所用的杠杆刻度和质量分布均匀,每个钩码相同。
(1)实验时,先把杠杆放在水平桌面上(如图甲所示),此时应将杠杆左、右两端的平衡螺母向 (选填“左”或“右”)移,直至杠杆在水平位置平衡。
(2)杠杆调节平衡后,在杠杆A处挂两个钩码(如图乙所示),要使杠杆重新平衡,此时应在B处挂 个钩码。
(3)若用弹簧测力计在C处沿竖直方向向上拉杠杆(如图丙所示),使杠杆在水平位置重新平衡,此时弹簧测力计的示数为 N;若将弹簧测力计逐渐向左斜拉(如图丁所示),使杠杆在水平位置仍然平衡,则拉力的力臂将 (选填“变大”、“不变”或“变小”)。杠杆平衡后,在整个实验过程中, (选填“可以”或“不可以”)再调节杠杆两端的平衡螺母。
(4)在实验中,多次改变力和力臂的大小主要是为了
A.减小摩擦
B.使实验数据更准确
C.多次测量求平均值可以减小误差
D.获取多组实验数据归纳出物理规律
能力提升
20.如图所示,用一根自重可忽略不计的撬棒撬石块,若撬棒C点受到石块的压力是1500 N,且AB=1 m,AD=0.5 m,CD=0.3 m,则要撬动该石块所用的最小的力是( )
A.900 N B.750 N C.300 N D.150 N
21.看漫画图,小猴和小兔在分萝卜,他们用一个三角形支点支起萝卜,当萝卜平衡时,小兔选择了长的那段萝卜,小猴选择了短的那段,请你分析一下小猴和小兔谁分的萝卜重?( )
A.小兔 B.小猴 C.一样重 D.无法判断
22.一个重为400 N的物体Q,底面积300 cm2,将其放在水平地面上,如图所示,现将物体Q挂在杠杆的B端,在A端悬挂一个重为200 N的物体P,使杠杆在水平位置平衡,忽略杠杆自重的影响,若OA:OB=1:2,那么( )
A.绳子对物体Q的拉力为150 N
B.地面对物体Q的支持力为200 N
C.绳子对物体P的拉力为250 N
D.物体Q对地面的压强是1×104 Pa
23.如图所示,将体积相同的甲、乙两球分别挂在轻质杠杆的AB两端,杠杆处于平衡状态,已知OB>OA;现将两球同时浸没在水中,下列说法正确的是( )
A.杠杆不能平衡,A端下沉
B.杠杆不能平衡,B端下沉
C.由于两球所受浮力大小相等,杠杆仍然不能平衡,B端下沉
D.两球质量未知,无法确定杠杆的平衡状态
24.如图是单塔双索斜拉大桥,索塔两侧对称的拉索承受了桥梁的重力,现仅有一辆载重汽车从桥梁左端速匀速驶向索塔的过程中,左侧拉索拉力大小( )
A.一直减小 B.一直增大
C.先减小后增大 D.保持不变
25.如图所示,有一根均匀铁棒,长为L,OA=,重力G=900 N,为了不使这根铁棒的B端下沉,所需外力F至少应为 N,若F的方向不变,微微抬起这根铁棒的B端,所需外力F′应为 N。
26.甲、乙两个身高相同的人抬着一个木箱沿斜坡上山,木箱的悬点恰好在抬杠的中央,如图1所示,则甲、乙两人所用的力F甲 F乙;如图2所示,甲、乙两人将一木箱从一楼抬上三楼,则甲、乙两人所用的力F甲 F乙(都选填大于、等于或小于)。
参考答案与试题解析
知识梳理
固定点;支点;动力;动力臂;阻力;阻力臂;F1L1=F2L2;>;<;费距离;独轮车、铡刀等;<;>;省距离;镊子、筷子等;=;=;不省距离;天平、定滑轮等。
基础知识
1.【解答】解:A.力臂不一定是杠杆的长度,力臂可能在杠杆上也可能不在杠杆上,故A错误;
B.力臂是从支点到力的作用线的距离,简单地说,就是“点到线”的距离,故B正确;
C.使用任何机械都不能省功,故C错误;
D.根据杠杆的平衡条件,杠杆平衡时,动力×动力臂与阻力×阻力臂总是相等的,故D错误。
故选:B。
2.【解答】解:
AB.因为动力的力臂的做法是过支点作动力作用线的垂线段,而A B选项中线段与动力作用线不垂直,故A.B都错;
C.图中,表示力臂的不是支点到动力作用线的垂线段,故C错;
D.图中表示的是支点到动力作用线的垂线段,故D正确。
故选:D。
3.【解答】解:设一个钩码重为G,杠杆一个小格是L,若将杠杆两侧所挂的钩码各取下一个,则左侧力与力臂的乘积为:1G×4L=4GL,右侧力与力臂的乘积为:3G×2L=6GL,因为4GL<6GL,根据杠杆平衡条件可知,杠杆不能平衡,且右端下沉,故B正确。
故选:B。
4.【解答】解:ABC.开瓶器、羊角锤、钳子在使用时,动力臂大于阻力臂,属于省力杠杆,省力费距离,故ABC错误;
D.筷子在使用时,动力臂小于阻力臂,属于费力杠杆,费力省距离,故D正确。
故选:D。
5.【解答】解:(1)把铁锨看作费力杠杆,杠杆是绕着C点转动,所以C点即为费力杠杆的支点;
(2)跷跷板在水平位置平衡时,设小明的重力为G1,力臂为L1,妈妈的重力为G2,力臂为L2,
因为G1L1=G2L2、G1<G2,所以L1>L2,即妈妈比小明离转轴近;
若小明远离转轴一小段距离,即力臂为L1变大,为了保持跷跷板水平平衡,由G1L1=G2L2知,在G1和G2不变时,L1变大,L2也变大,妈妈应适当远离转轴。
故答案为:C;近;远。
6.【解答】解:
①撬棒在使用过程中,动力臂大于阻力臂,是省力杠杆;
②天平在使用过程中,动力臂等于阻力臂,是等臂杠杆
③筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;
④铡刀在使用过程中,动力臂大于阻力臂,是省力杠杆;
⑤镊子在使用过程中,动力臂小于阻力臂,是费力杠杆;
⑥瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;
⑦钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;
所以省力的杠杆有①④⑥;费力的杠杆有③⑤⑦。
故答案为:①④⑥;③⑤⑦。
7.【解答】解:由图示可知,O为支点,地面对手的支持力的力臂:
L=0.4 m+0.8 m=1.2 m;
由杠杆平衡条件得:FL=GLG,即:F×1.2 m =600 N×0.8 m,
解得:F=400 N。
故答案为:1.2;400。
8.【解答】解:如图所示,O为支点,延长拉力F1的作用线,从点O到F1的作用线作垂线,即为F1的力臂l1;由题可知,重物对杠杆的拉力为阻力F2,方向为竖直向下;如下图所示:
9.【解答】解:取碗夹子在使用过程中,动力臂小于阻力臂,是费力杠杆;核桃夹子、羊角锤、修枝剪刀在使用过程中,动力臂大于阻力臂,是省力杠杆;故A与其他三个不同。
故选:A。
10.【解答】解:苹果和桔子对杠杆的拉力分别为动力和阻力,由图知,动力臂小于阻力臂,根据杠杆平衡条件知,动力大于阻力,因此使杠杆逆时针转动的力是杠杆左端苹果对杆的拉力。
故选:C。
11.【解答】解:两次抬起水泥板时,动力克服的都是水泥板的重力,对于形状规则质地均匀的物体,其重心都在其几何中心上,所以阻力臂都等于动力臂的二分之一,即动力臂都是阻力臂的2倍。
根据杠杆的平衡条件可得:F==G,所以前后两次所用的力相同,故ABC错误,D正确。
故选:D。
12.【解答】解:由图可知车厢绕着点C转动,所以C点为支点;
当物体A放在车厢的后部时,动力臂大于阻力臂,因此省力,所以选项A、B、C都不正确。
故选:D。
13.【解答】解:由题知,杠杆的支点在O处,绳的拉力沿绳方向画,从支点向力的作用线引垂线,如图所示:
故选:C。
14.【解答】解:
由图可知,O为支点,阻力为物体的重力G,由于F始终垂直于杠杆,所以动力臂不变;将杠杆缓慢地由最初位置拉到水平位置时,动力臂不变,阻力不变,阻力臂变大,根据杠杆平衡条件F1L1=F2L2可知,动力变大;
将杠杆从水平位置拉到最终位置时,动力臂不变,阻力不变,阻力臂变小,根据杠杆平衡条件F1L1=F2L2可知,动力变小;所以,在整个过程中,F先变大后变小。
故选:B。
15.【解答】解:支点是杠杆绕着转动的固定点,由图可知,当前轮遇障碍物A时,顾客向下按扶把,这时手推车可绕C点转动,故支点是C点;
当后轮遇到障碍物A时,顾客向上提把,这时手推车可绕B点转动,故支点是B点。
故答案为:C;B。
16.【解答】解:(1)要使横杆AB保持水平平衡,则在A端施加最小力的方向应该竖直向下的;
横杆AB粗细相同、质量分布均匀,所以其重心C在几何中心上,支点为O,则OA就是动力臂,OC就是阻力臂,如下图所示:
已知AB=2.8 m,AO=0.3 m,则阻力臂OC=AB﹣OA=×2.8 m﹣0.3 m=1.1 m,
由杠杆的平衡条件可得:F×OA=G×OC,
则F===440 N。
(3)由题意可知,动力臂AO小于阻力臂OC,为费力杠杆。
故答案为:下;440;费力。
17.【解答】解:杠杆在图示位置平衡,阻力G与阻力臂OA一定,由杠杆平衡条件可知,在阻力与阻力臂一定时,动力臂越大,动力越小,由图示可知,OB为最大动力臂,此时动力最小,过B点作垂直于OB向下的动力F1即可;
重物对杠杆的拉力即为阻力,过A点作竖直向下的力即为阻力F2,如图所示:
18.【解答】解:过L1的上端作力臂L1的垂线即力F1的作用线,与杠杆的交点就是动力的作用点,动力和阻力使杠杆转动的效果相反,则动力F1的方向向上;
由图可知,O为支点,物体对杠杆的拉力是阻力F2,由O向力F2的作用线引垂线,支点到垂足的距离就是力臂L2。如下图所示:
19.【解答】解:(1)因为图甲中杠杆的右端下倾,所以应将两侧的平衡螺母向左移动,使杠杆在水平位置平衡;
(2)设杠杆每一个小格为L,每个钩码的重力为G,
根据杠杆平衡条件F1L1=F2L2得,2G×2L=nG×4L,所以n=1,所以在B处挂1个钩码;
(3)由图丙可知,弹簧测力计的分度值为0.1 N,所以此时弹簧测力计的示数为1.9 N;
当弹簧测力计倾斜拉杠杆时,拉力的力臂小于OC,拉力的力臂变小;
实验过程中,螺母再调节会改变杠杆重心的位置,使杠杆重力对杠杆平衡又产生影响,因此不能再调节平衡螺母;
(4)探究杠杆平衡的条件时,多次改变力和力臂的大小主要是为了获取多组实验数据,排除偶然性,得到普遍规律;故ABC错误,D正确。
故答案为:(1)左;(2)1;(3)1.9;变小;不可以;(4)D。
20.【解答】解:
①若以D点为支点,则作用在A点的最小力应垂直于杠杆斜向下,此时AD为动力臂,CD为阻力臂,如图:
②若以B点为支点,则作用在A点的最小力应垂直于杠杆斜向上,此时AB为动力臂,BC为阻力臂,如图:
由图知,AD<AB,CD>BC,所以②更省力;
如上图,以B为支点,动力臂AB=1 m,阻力臂BC=AB﹣AD﹣CD=1 m﹣0.5 m﹣0.3 m=0.2 m,
由杠杆的平衡条件得:F1×AB=F2×BC,
即:F1×1 m=1500 N×0.2 m,
解得F1=300 N,故C正确。
故选:C。
21.【解答】解:萝卜处于平衡状态,如图所示:
右侧部分重心离支点O较远,故力臂OB较大,左侧部分重心离支点O较近,故力臂OA较小;
根据杠杆平衡条件G1×OA=G2×OB,因为OB>OA,所以G1>G2,
所以小兔选择的那段长萝卜的重力比另一段小些,故B正确。
故选:B。
22.【解答】解:在A端悬挂一个重为200 N的物体P,P处于静止状态,则绳子对物体P的拉力为200 N,故C错误;
杠杆水平位置平衡,由杠杆平衡条件可得:GP OA=FB OB,
杠杆B点受到的拉力:FB=GP=×200 N=100 N,
因相互作用力大小相等,所以,绳子对物体Q的拉力F拉=FB=100 N,故A错误;
因物体Q受到竖直向上绳子的拉力和地面的支持力、竖直向下重力的作用下处于平衡状态,
所以,由力的平衡条件可得:F支持=GQ﹣F拉=400 N﹣100 N=300 N,故B错误;
因地面对Q的支持力和物体Q对地面的压力是一对相互作用力,
所以,物体Q对地面的压力:F压=F支持=300 N,
物体Q对地面的压强:p===1×104 Pa,故D正确。
故选:D。
23.【解答】解:物体没有浸入水中时,根据杠杆平衡条件有G甲×OA=G乙×OB,由图可见OA<OB,则G甲>G乙。物体浸入水中时,对杠杆的拉力F=G﹣F浮,因为两个物体的体积相等,都同时浸没在水中,所以它们受到的浮力相等,即F浮甲=F浮乙;
杠杆A端:(G甲﹣F浮甲)×OA=G甲×OA﹣F浮甲×OA,
杠杆B端:(G乙﹣F浮乙)×OB=G乙×OB﹣F浮乙×OB,
因OA<OB,则F浮甲×OA<F浮乙×OB;又G甲×OA=G乙×OB,
则(G甲×OA﹣F浮甲×OA)>(G乙×OB﹣F浮乙×OB),
因此杠杆的左(A)端下降。
故选:A。
24.【解答】解:以索塔与桥面的交点为支点,左侧拉索的拉力为动力,汽车对桥的压力为阻力,当载重汽车从桥梁左端匀速驶向索塔的过程中,阻力臂逐渐减小,在阻力和动力臂不变时,根据杠杆的平衡条件知左侧拉索拉力大小一直减小,故A正确。
故选:A。
25.【解答】解:
(1)为了不使这根铁棒的B端下沉,此时杠杆的支点是A,动力臂为AB=L+L=L,阻力臂为AO=L,
根据杠杆的平衡条件可得:F×L=G L,所以F=G=×900 N=400 N;
(2)微微抬起这根铁棒的B端,此时支点是C,动力臂为CB=L,阻力臂为CO=L,
根据杠杆的平衡条件可得:F′ L=G×;所以F′===450 N;
故答案为:400;450。
26.【解答】解:(1)如图所示:
LAE为阻力臂,LAF为动力臂;因为:F乙LAF=GLAE,所以:F乙==G,
同理,可求F甲=G,则甲、乙两人所用的力F甲=F乙;
(2)为了方便分析,以木箱的重心为支点(也可以以任何一个人的手为支点),两人施加的力都是竖直向上的,力和力臂的情况如下图所示:
由图可知,L甲<L乙,根据杠杆平衡条件可得:F甲L甲=F乙L乙,
所以可知F甲>F乙。
故答案为:等于;大于。
1
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
