人教版九年级数学下册 29.2 三视图(3) 教学课件(共19张PPT)
文档属性
| 名称 | 人教版九年级数学下册 29.2 三视图(3) 教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 324.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 17:51:21 | ||
图片预览




文档简介
(共19张PPT)
第二十九章投影与视图
29.2三视图
第3课时
由三视图抽象出立体图形、由立体图形的展开图计算表面积、体积等,进一步发展空间想象能力.
学习目标
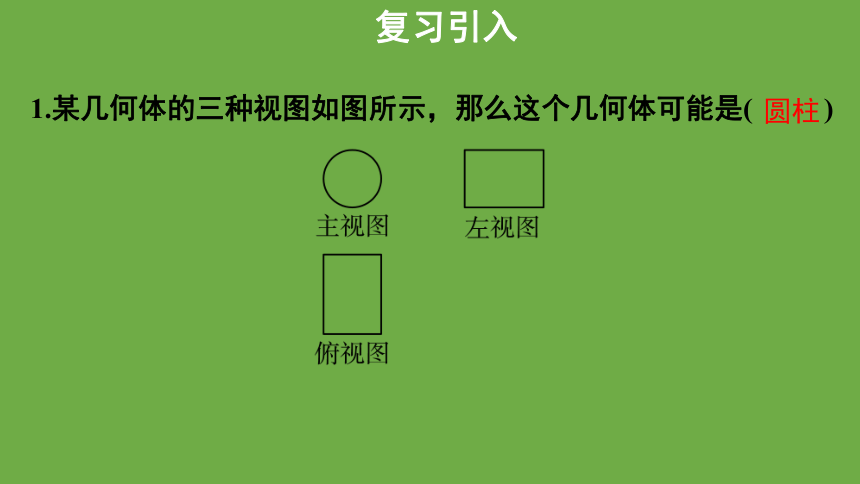
1.某几何体的三种视图如图所示,那么这个几何体可能是( )
圆柱
复习引入
2.如图是某个几何体的三视图,则该几何体是( )
三棱柱
复习引入
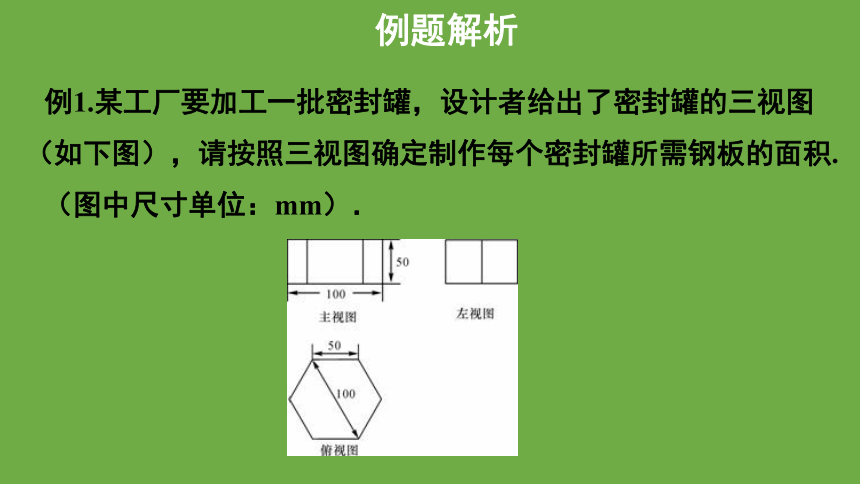
例1.某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积.
(图中尺寸单位:mm).
例题解析
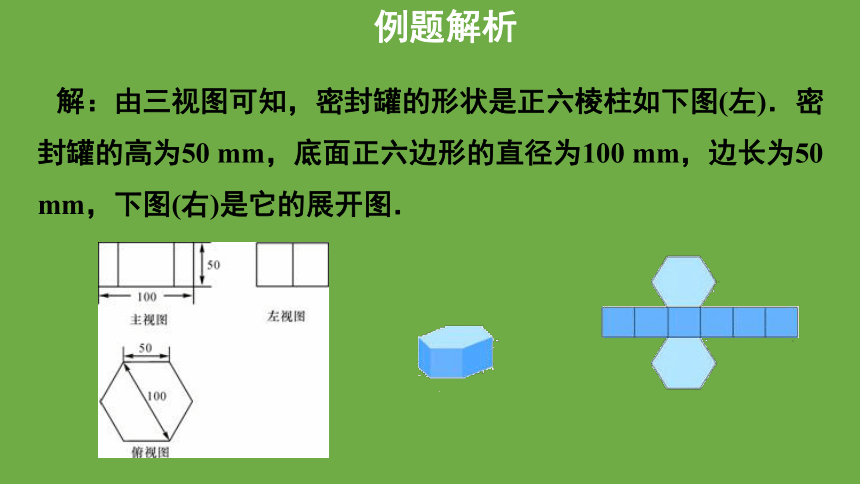
解:由三视图可知,密封罐的形状是正六棱柱如下图(左).密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,下图(右)是它的展开图.
例题解析
由展开图可知,制作一个密封罐所需钢板的面积为
.
例题解析
例2. 某游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图,已知正方体的棱长与圆柱的直径及高
相等,都是0.8 m.
(1)请画出它的主视图、左视图、俯视图;
(2)为了美观,需要在这个立体图形的表
面刷一层油漆,已知油漆每平方米40元,
那么一共需要花费多少元 (结果精确到0.1)
例题解析
分析:该几何体是一个组合体,
下边是正方体,上边是圆柱体,
可以较容易地画出三视图,已知
圆柱的和底面直径等于正方体的
棱长,即可求出组合体的表面积,
就可以求出总费用.
解:三视图如右图所示:
例题解析
(2)根据题意得,这个立体图形的表面积为0.8×0.8×5+0.8π×0.8=(0.64π+3.2)m2,
则一共需要花费40×(0.64π+3.2)≈208.4(元).
答:一共需要花费约208.4元.
例题解析
1. 一个空心圆柱体,其主视图正确的是( )
B
课堂练习
2.已知某几何体的三视图如图所示,其中俯视图为等边三角形,
则该几何体的左视图的面积为 .
课堂练习
3.一个几何体的三视图如图所示,根据图中的数据计算
该几何体的体积为 .(结果保留π)
12π
课堂练习
4.一个几何体的三视图如图所示,求这个这个几何体的表面积.
分析:由三视图可知该几何体为
组合体:主视图是长为10、宽为60
的长方形和长为20、高为50的长方形
组合;俯视图是长为60、宽为40的
长方形;左视图是长为40、高为60的
长方形,将这些图形的面积求和即可.
解:主视图的面积=10×60+50×20=1 600,
左视图的面积=40×(50+10)=2 400
俯视图的面积=40×(20+20+20)=2 400,
∴这个几何体的表面积=2×(1 600+2 400+2 400)=12 800.
课堂练习
5.如图所示的是某种型号的正六角螺母毛坯的三视图,求它的表面积.
解:侧面积=6×3×2=36(cm2),底面可以看成
由2个等腰梯形组成的,它们的高是
所以两个底面积是2×2×
表面积=
课堂练习
6.一个几何体的三视图如图所示,它的俯视图为菱形,
请写出该几何体的形状,并根据图中数据计算它的侧面积.
解:该几何体的形状是四棱柱,由三视图
知棱柱底面菱形的对角线长分别
为4 cm,3 cm.根据菱形的对角线互相
垂直平分,得菱形的边长为
所以该几何体的侧面积为:
课堂练习
根据三视图求几何体的侧面积、体积的一般步骤:
(1)根据三视图推断出几何体的形状 “由图到物”.
(2)结合图中给出的数据,正确求出相关元素的值.
(3)根据计算公式和已求出的数据,从而求得表面积、体积等.
课堂小结
再见
第二十九章投影与视图
29.2三视图
第3课时
由三视图抽象出立体图形、由立体图形的展开图计算表面积、体积等,进一步发展空间想象能力.
学习目标
1.某几何体的三种视图如图所示,那么这个几何体可能是( )
圆柱
复习引入
2.如图是某个几何体的三视图,则该几何体是( )
三棱柱
复习引入
例1.某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积.
(图中尺寸单位:mm).
例题解析
解:由三视图可知,密封罐的形状是正六棱柱如下图(左).密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,下图(右)是它的展开图.
例题解析
由展开图可知,制作一个密封罐所需钢板的面积为
.
例题解析
例2. 某游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图,已知正方体的棱长与圆柱的直径及高
相等,都是0.8 m.
(1)请画出它的主视图、左视图、俯视图;
(2)为了美观,需要在这个立体图形的表
面刷一层油漆,已知油漆每平方米40元,
那么一共需要花费多少元 (结果精确到0.1)
例题解析
分析:该几何体是一个组合体,
下边是正方体,上边是圆柱体,
可以较容易地画出三视图,已知
圆柱的和底面直径等于正方体的
棱长,即可求出组合体的表面积,
就可以求出总费用.
解:三视图如右图所示:
例题解析
(2)根据题意得,这个立体图形的表面积为0.8×0.8×5+0.8π×0.8=(0.64π+3.2)m2,
则一共需要花费40×(0.64π+3.2)≈208.4(元).
答:一共需要花费约208.4元.
例题解析
1. 一个空心圆柱体,其主视图正确的是( )
B
课堂练习
2.已知某几何体的三视图如图所示,其中俯视图为等边三角形,
则该几何体的左视图的面积为 .
课堂练习
3.一个几何体的三视图如图所示,根据图中的数据计算
该几何体的体积为 .(结果保留π)
12π
课堂练习
4.一个几何体的三视图如图所示,求这个这个几何体的表面积.
分析:由三视图可知该几何体为
组合体:主视图是长为10、宽为60
的长方形和长为20、高为50的长方形
组合;俯视图是长为60、宽为40的
长方形;左视图是长为40、高为60的
长方形,将这些图形的面积求和即可.
解:主视图的面积=10×60+50×20=1 600,
左视图的面积=40×(50+10)=2 400
俯视图的面积=40×(20+20+20)=2 400,
∴这个几何体的表面积=2×(1 600+2 400+2 400)=12 800.
课堂练习
5.如图所示的是某种型号的正六角螺母毛坯的三视图,求它的表面积.
解:侧面积=6×3×2=36(cm2),底面可以看成
由2个等腰梯形组成的,它们的高是
所以两个底面积是2×2×
表面积=
课堂练习
6.一个几何体的三视图如图所示,它的俯视图为菱形,
请写出该几何体的形状,并根据图中数据计算它的侧面积.
解:该几何体的形状是四棱柱,由三视图
知棱柱底面菱形的对角线长分别
为4 cm,3 cm.根据菱形的对角线互相
垂直平分,得菱形的边长为
所以该几何体的侧面积为:
课堂练习
根据三视图求几何体的侧面积、体积的一般步骤:
(1)根据三视图推断出几何体的形状 “由图到物”.
(2)结合图中给出的数据,正确求出相关元素的值.
(3)根据计算公式和已求出的数据,从而求得表面积、体积等.
课堂小结
再见
