人教版九年级数学下册 反比例函数综合提升(共17张PPT)
文档属性
| 名称 | 人教版九年级数学下册 反比例函数综合提升(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 833.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
《反比例函数》章综合
综合提升
综合提升
解:∵k 0,
反比例函数y= (k 0)的图象有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),
若x1 x2 0 x3 ,则下列结论正确的是( )
A. y1 y2 y3 B. y3 y1 y2 C. y3 y2 y1 D. y1 y3 y2
例1
∴y= 图象在第二、四象限,且在每个象限内,y随x的增大而增大.
∵x1 x2 0,
∴P1(x1,y1),P2(x2,y2)都在第二象限内,
∴0 y1 y2.
∵x3 0,
∴P3(x3,y3)在第四象限内,
∴y3 0.
∴y3 y1 y2.
函数性质
特殊值
设y=
y3 y1 y2
取x1 2,x2 1,x3 1
得y1 1,y2 2,y3 2
B
综合提升 反比例函数的图象与性质
综合提升
综合提升 反比例函数的图象与性质
解:反比例函数y= (k 0)的大致图象如右图,
P2
∵x1 x2 0 x3,
∴P1,P2,P3的位置大致如图.
结合图象可得:y3 y1 y2.
P1
x2
y2
x1
y1
x
y
O
x3
y3
P3
数形结合
要点概括
知识本质 以形助数,以数解形
反比例函数y= (k 0)的图象有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),
若x1 x2 0 x3 ,则下列结论正确的是( )
A. y1 y2 y3 B. y3 y1 y2 C. y3 y2 y1 D. y1 y3 y2
例1
B
综合提升
解:由反比例函数k的几何意义可得:
x
y
O
A4
A2
A5
A3
A1
如图,在x轴的正半轴上依次截取OA1 A1A2 A2A3 A3A4 A4A5…,过A1,A2,A3,A4,A5…分别作x轴的垂线与反比例函数y 的图象交于点P1,P2,P3,P4,P5…,设△OA1P1、△A1A2P2、△A2A3P3…的面积分别为S1,S2,S3… Sn ,则Sn的值为 (n为正整数).
例2
P4
P2
P5
P3
P1
又因为OA1 A1A2 A2A3 A3A4 A4A5…
以此类推, .
综合提升 反比例函数k的几何意义
推理能力
综合提升
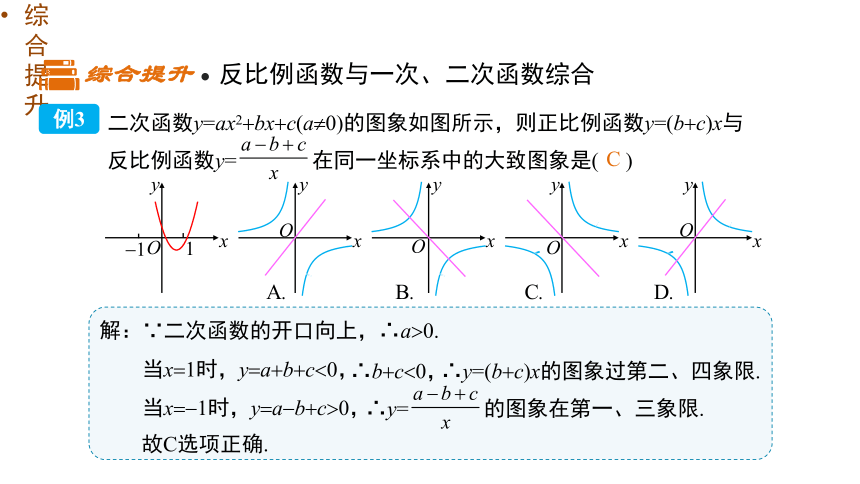
综合提升 反比例函数与一次、二次函数综合
二次函数y=ax2 bx c(a 0)的图象如图所示,则正比例函数y=(b c)x与反比例函数y= 在同一坐标系中的大致图象是( )
解:∵二次函数的开口向上,∴a 0.
当x 1时,y a b c 0,
当x 1时,y a b c 0,
故C选项正确.
x
y
O
x
y
O
x
y
O
1
1
x
y
O
x
y
O
A.
B.
C.
D.
∴b c 0,
∴y=(b c)x的图象过第二、四象限.
∴y= 的图象在第一、三象限.
C
例3
综合提升
解:
(1)由 解得 或
y
y x 2
y1 3
x1 1
y2 1
x2 3
如图,已知一次函数y x 2与反比例函数y 的图象交于A、B两点.
(1)求A、B两点的坐标;(2)求△AOB的面积.
例4
x
y
O
B
A
C
即A的坐标是(3,1),B的坐标是( 1, 3).
(2)设函数y x 2与y轴的交点是C,
当x 0时,y 2,
∴C(0, 2).
∴S△AOB S△AOC S△BOC OC (xA |xB|) 2 (3 1) 4.
综合提升 反比例函数与一次函数综合
综合提升
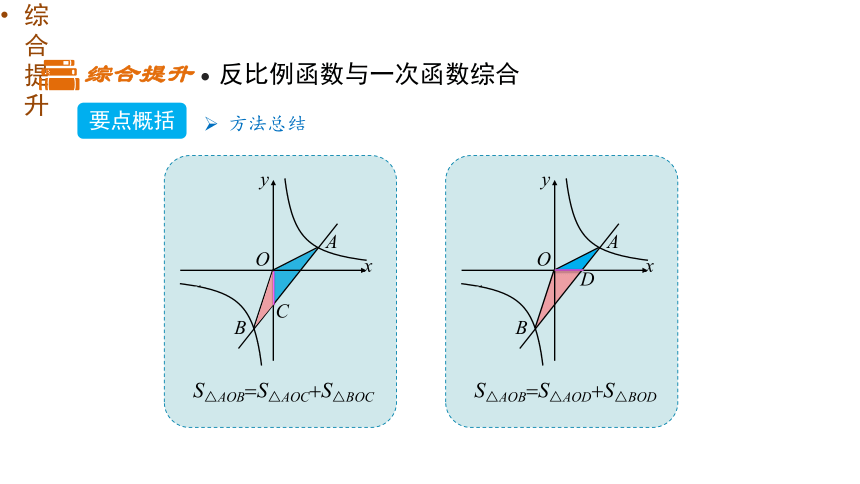
要点概括
方法总结
综合提升 反比例函数与一次函数综合
x
y
O
B
A
C
S△AOB S△AOC S△BOC
D
S△AOB S△AOD S△BOD
x
y
O
B
A
综合提升
要点概括
方法总结
x
y
O
B
A
C
D
E
x
y
O
B
A
x
y
O
B
A
S△AOB S矩形OCDE S△OEA
S△OBC S△ABD
S△AOB S梯形ABDC
S△AOB S△AOC S△BOC
S△BOD S△AOD
D
C
D
C
综合提升 反比例函数与一次函数综合
综合提升
综合提升 实际问题与反比例函数
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(1)分别求该化工厂治污期间及治污改造工程完工后y与x之间的函数关系式;
例5
解:(1)当1≤x≤5时,设y ,
把(1,200)代入,得k 200,即y .
当x 5时,y 40 20(x 5) 20x 60.
综上, y与x之间的函数关系式为
x/月
y/万元
O
1
5
200
160
120
80
40
y (1≤x≤5),
y 20x 60(x≥5).
推理能力
综合提升
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2019年1月的水平?
例5
解:(2)当y 200时,20x 60 200,解得x 13.
因为13 5 8,所以治污改造工程完工后经过8个月,该厂月利润才能达到2019年1月的水平.
x/月
y/万元
O
1
5
200
160
120
80
40
综合提升 实际问题与反比例函数
综合提升
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(3)当月利润少于100万元时为该厂资金紧张期,该厂资金紧张期共有几个月?
例5
解:(3)对于y ,当y 100时,x 2.
对于y 20x 60,当y 100时,x 8.
所以该厂资金紧张期共有5个月.
x/月
y/万元
O
1
5
200
160
120
80
40
综合提升 实际问题与反比例函数
综合提升
要点概括
解题步骤
实际问题
建立反比例函
数模型求解
实际问题的解
审
设
列
写
解
审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系.
根据常量与变量之间的关系,设出函数解析式,待定的系数用字母表示.
由题目中的已知条件列出方程,求出待定系数.
写出函数解析式,并注意解析式中变量的取值范围.
用反比例函数的图象与性质解决实际问题.
综合提升 实际问题与反比例函数
综合提升
解:(1)∵反比例函数y= 的图象经过点D(3,1),
∴k 3 1 3.
∴反比例函数的解析式为y= .
综合提升 反比例函数与特殊四边形结合
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的解析式;
例6
G
E
B
D
F
x
y
O
A
C
综合提升
解:(2)①∵D为BC的中点,∴BC 2.
∵△ABC与△EFG成中心对称,∴△ABC与≌△EFG,
∴GF BC 2,GE AC 1.
∵点E在反比例函数的图象上,∴E(1,3),即OG 3,
∴OF OG GF 1.
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.①求OF的长;
G
E
B
D
F
x
y
O
A
C
例6
综合提升 反比例函数与特殊四边形结合
综合提升
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
例6
②连接AF,BE,证明四边形ABEF是正方形.
解:(2)②∵AC 1,OC 3,∴OA 2 GF.
在△AOF和△FGE中,
OA GF, AOF FGE,OF GE.
∴△AOF≌△FGE(SAS),
∴ GFE FAO, BAC GEF AFO,AF EF AB.
G
E
B
D
F
x
y
O
A
C
综合提升 反比例函数与特殊四边形结合
综合提升
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
例6
②连接AF,BE,证明四边形ABEF是正方形.
解:∴ GFE AFO FAO BAC FAO AFO 90°.
∴ EFA BAF 90°.
又∵EF AB,
又∵EF AF,且 EFA 90°.
∴四边形ABEF为正方形.
G
E
B
D
F
x
y
O
A
C
∴EF//AB.
∴四边形ABEF为平行四边形.
综合提升 反比例函数与特殊四边形结合
再 见
《反比例函数》章综合
综合提升
综合提升
解:∵k 0,
反比例函数y= (k 0)的图象有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),
若x1 x2 0 x3 ,则下列结论正确的是( )
A. y1 y2 y3 B. y3 y1 y2 C. y3 y2 y1 D. y1 y3 y2
例1
∴y= 图象在第二、四象限,且在每个象限内,y随x的增大而增大.
∵x1 x2 0,
∴P1(x1,y1),P2(x2,y2)都在第二象限内,
∴0 y1 y2.
∵x3 0,
∴P3(x3,y3)在第四象限内,
∴y3 0.
∴y3 y1 y2.
函数性质
特殊值
设y=
y3 y1 y2
取x1 2,x2 1,x3 1
得y1 1,y2 2,y3 2
B
综合提升 反比例函数的图象与性质
综合提升
综合提升 反比例函数的图象与性质
解:反比例函数y= (k 0)的大致图象如右图,
P2
∵x1 x2 0 x3,
∴P1,P2,P3的位置大致如图.
结合图象可得:y3 y1 y2.
P1
x2
y2
x1
y1
x
y
O
x3
y3
P3
数形结合
要点概括
知识本质 以形助数,以数解形
反比例函数y= (k 0)的图象有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),
若x1 x2 0 x3 ,则下列结论正确的是( )
A. y1 y2 y3 B. y3 y1 y2 C. y3 y2 y1 D. y1 y3 y2
例1
B
综合提升
解:由反比例函数k的几何意义可得:
x
y
O
A4
A2
A5
A3
A1
如图,在x轴的正半轴上依次截取OA1 A1A2 A2A3 A3A4 A4A5…,过A1,A2,A3,A4,A5…分别作x轴的垂线与反比例函数y 的图象交于点P1,P2,P3,P4,P5…,设△OA1P1、△A1A2P2、△A2A3P3…的面积分别为S1,S2,S3… Sn ,则Sn的值为 (n为正整数).
例2
P4
P2
P5
P3
P1
又因为OA1 A1A2 A2A3 A3A4 A4A5…
以此类推, .
综合提升 反比例函数k的几何意义
推理能力
综合提升
综合提升 反比例函数与一次、二次函数综合
二次函数y=ax2 bx c(a 0)的图象如图所示,则正比例函数y=(b c)x与反比例函数y= 在同一坐标系中的大致图象是( )
解:∵二次函数的开口向上,∴a 0.
当x 1时,y a b c 0,
当x 1时,y a b c 0,
故C选项正确.
x
y
O
x
y
O
x
y
O
1
1
x
y
O
x
y
O
A.
B.
C.
D.
∴b c 0,
∴y=(b c)x的图象过第二、四象限.
∴y= 的图象在第一、三象限.
C
例3
综合提升
解:
(1)由 解得 或
y
y x 2
y1 3
x1 1
y2 1
x2 3
如图,已知一次函数y x 2与反比例函数y 的图象交于A、B两点.
(1)求A、B两点的坐标;(2)求△AOB的面积.
例4
x
y
O
B
A
C
即A的坐标是(3,1),B的坐标是( 1, 3).
(2)设函数y x 2与y轴的交点是C,
当x 0时,y 2,
∴C(0, 2).
∴S△AOB S△AOC S△BOC OC (xA |xB|) 2 (3 1) 4.
综合提升 反比例函数与一次函数综合
综合提升
要点概括
方法总结
综合提升 反比例函数与一次函数综合
x
y
O
B
A
C
S△AOB S△AOC S△BOC
D
S△AOB S△AOD S△BOD
x
y
O
B
A
综合提升
要点概括
方法总结
x
y
O
B
A
C
D
E
x
y
O
B
A
x
y
O
B
A
S△AOB S矩形OCDE S△OEA
S△OBC S△ABD
S△AOB S梯形ABDC
S△AOB S△AOC S△BOC
S△BOD S△AOD
D
C
D
C
综合提升 反比例函数与一次函数综合
综合提升
综合提升 实际问题与反比例函数
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(1)分别求该化工厂治污期间及治污改造工程完工后y与x之间的函数关系式;
例5
解:(1)当1≤x≤5时,设y ,
把(1,200)代入,得k 200,即y .
当x 5时,y 40 20(x 5) 20x 60.
综上, y与x之间的函数关系式为
x/月
y/万元
O
1
5
200
160
120
80
40
y (1≤x≤5),
y 20x 60(x≥5).
推理能力
综合提升
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2019年1月的水平?
例5
解:(2)当y 200时,20x 60 200,解得x 13.
因为13 5 8,所以治污改造工程完工后经过8个月,该厂月利润才能达到2019年1月的水平.
x/月
y/万元
O
1
5
200
160
120
80
40
综合提升 实际问题与反比例函数
综合提升
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2019年1月的利润为200万元,设2019年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2019年1月起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元.
(3)当月利润少于100万元时为该厂资金紧张期,该厂资金紧张期共有几个月?
例5
解:(3)对于y ,当y 100时,x 2.
对于y 20x 60,当y 100时,x 8.
所以该厂资金紧张期共有5个月.
x/月
y/万元
O
1
5
200
160
120
80
40
综合提升 实际问题与反比例函数
综合提升
要点概括
解题步骤
实际问题
建立反比例函
数模型求解
实际问题的解
审
设
列
写
解
审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系.
根据常量与变量之间的关系,设出函数解析式,待定的系数用字母表示.
由题目中的已知条件列出方程,求出待定系数.
写出函数解析式,并注意解析式中变量的取值范围.
用反比例函数的图象与性质解决实际问题.
综合提升 实际问题与反比例函数
综合提升
解:(1)∵反比例函数y= 的图象经过点D(3,1),
∴k 3 1 3.
∴反比例函数的解析式为y= .
综合提升 反比例函数与特殊四边形结合
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的解析式;
例6
G
E
B
D
F
x
y
O
A
C
综合提升
解:(2)①∵D为BC的中点,∴BC 2.
∵△ABC与△EFG成中心对称,∴△ABC与≌△EFG,
∴GF BC 2,GE AC 1.
∵点E在反比例函数的图象上,∴E(1,3),即OG 3,
∴OF OG GF 1.
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.①求OF的长;
G
E
B
D
F
x
y
O
A
C
例6
综合提升 反比例函数与特殊四边形结合
综合提升
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
例6
②连接AF,BE,证明四边形ABEF是正方形.
解:(2)②∵AC 1,OC 3,∴OA 2 GF.
在△AOF和△FGE中,
OA GF, AOF FGE,OF GE.
∴△AOF≌△FGE(SAS),
∴ GFE FAO, BAC GEF AFO,AF EF AB.
G
E
B
D
F
x
y
O
A
C
综合提升 反比例函数与特殊四边形结合
综合提升
如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上, ACB 90°,AC 1.反比例函数y= (k 0)的图象经过BC边的中点D(3,1).
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
例6
②连接AF,BE,证明四边形ABEF是正方形.
解:∴ GFE AFO FAO BAC FAO AFO 90°.
∴ EFA BAF 90°.
又∵EF AB,
又∵EF AF,且 EFA 90°.
∴四边形ABEF为正方形.
G
E
B
D
F
x
y
O
A
C
∴EF//AB.
∴四边形ABEF为平行四边形.
综合提升 反比例函数与特殊四边形结合
再 见
