人教版九年级数学下册 27.3位似 教学课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.3位似 教学课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 20:36:30 | ||
图片预览




文档简介
(共17张PPT)
第二十七章 相似
27.3 位似
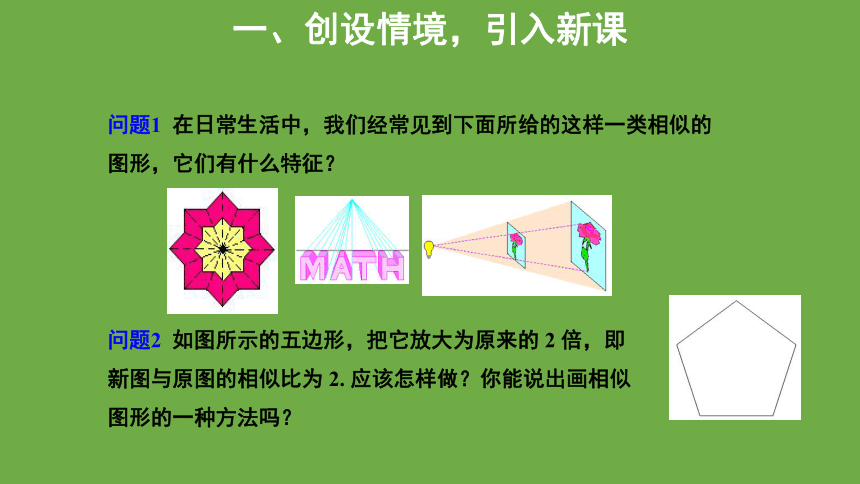
问题1 在日常生活中,我们经常见到下面所给的这样一类相似的图形,它们有什么特征?
问题2 如图所示的五边形,把它放大为原来的 2 倍,即新图与原图的相似比为 2. 应该怎样做?你能说出画相似图形的一种方法吗?
一、创设情境,引入新课
问题3 观察下图,图中有多边形相似吗?如果有,那么这种相似什么共同的特征?
位似图形的概念:每幅图的两个多边形不仅是相似图形,而且是每组对应点连线相交于一点,像这样的两个图形叫做位似图形.这个点叫做位似中心.这时我们说这两个图形关于这点位似.
二、合作交流,探究新知
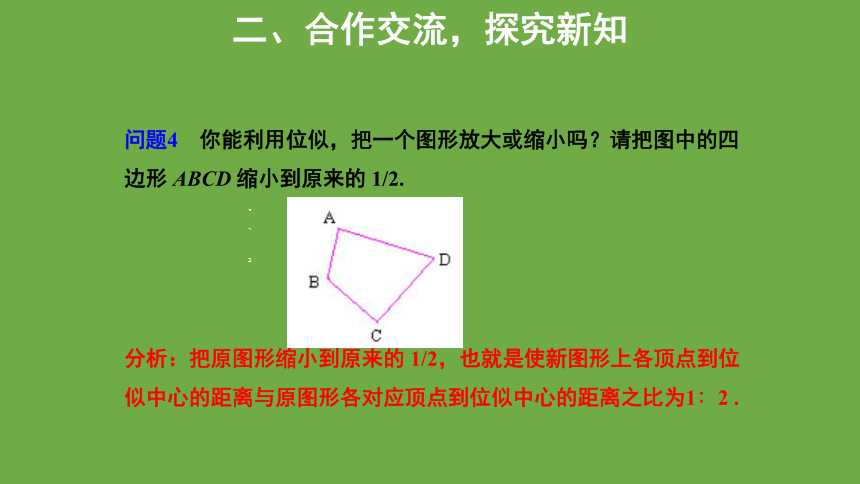
问题4 你能利用位似,把一个图形放大或缩小吗?请把图中的四边形 ABCD 缩小到原来的 1/2.
分析:把原图形缩小到原来的 1/2,也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2 .
二、合作交流,探究新知
作法一:(1)在四边形 ABCD 外任取一点O;
(2)过点 O 分别作射线OA,OB,OC,OD;
(3)分别在射线 OA,OB,OC,OD上取点A′、B′、C′、D′,
使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
追问:你还有其它方法作出符合条件的图形吗?
二、合作交流,探究新知
作法二:(1)在四边形 ABCD 外任取一点 O;
(2)过点 O 分别作射线 OA, OB, OC,OD;
(3)分别在射线 OA, OB, OC, OD 的反向延长线上取点A′、B′、C′、D′,使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
二、合作交流,探究新知
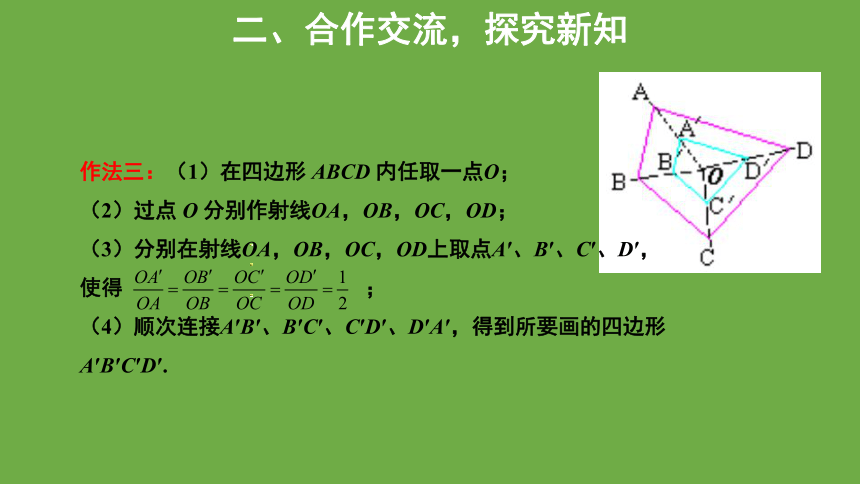
作法三:(1)在四边形 ABCD 内任取一点O;
(2)过点 O 分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,
使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
二、合作交流,探究新知
二、合作交流,探究新知
问题6 至此,我们已经学移、轴对称、旋转和位似等图形的变化方式.在下面的图案中,你能找出平移、轴对称、旋转和位似这些变换吗?
二、合作交流,探究新知
追问:还可以得到其它图形吗?自己试一试.
三、运用新知
三、运用新知
1. 下列说法正确的是( )
A. 相似的两个五边形一定是位似图形
B. 两个大小不同的正三角形一定是位似图形
C. 两个位似图形一定是相似图形
D. 所有的正方形都是位似图形
解析:位似图形是相似图形的特例,相似图形不一定是位似图形,故答案应选择 C.
C
四、巩固新知
2. 两个位似多边形一对对应顶点到位似中心的距离比为1∶2,且它们面积和为80,则较小的多边形的面积是( )
A. 16 B. 32 C. 48 D. 64
解析:位似图形必定相似,具备相似形的性质,其相似比等于一对对应顶点到位似中心的距离比.相似比为1∶2,则面积比为1∶4,由面积和为80,得到它们的面积分别为16,64. 故答案应选择 A.
A
四、巩固新知
四、巩固新知
3. 如图, △ABC 三个顶点坐标分别为A(2 , 3), B(2, 1), C(6, 2).
(1)将△ABC 向左平移三个单位得到△A1B1C1 ,写出A1、B1、C1三点的坐标;
(2)写出△ABC 关于 x 轴对称的△A2B2C2 三个顶点A2、B2、C2的坐标;
(3)将△ABC 绕点 O 旋转180°得到△A3B3C3 ,写出A3、B3、 C3三点的坐标.
4. 利用位似的方法把下图缩小到原来的一半,要求所作的图形在原图内部.
答案:
四、巩固新知
回顾本节课的学习,回答下列问题:
1. 什么样的图形叫做位似图形?位似中心是什么?
2. 利用位似如何给一个多边形放大或缩小?
3. 在直角坐标系中,如何研究两个位似图形对应点的坐标之间的关系?
4. 我们以前学过的平移、对称、旋转变换,它们的特点是什么?位似变换的特点是什么?
五、归纳小结
再 见
第二十七章 相似
27.3 位似
问题1 在日常生活中,我们经常见到下面所给的这样一类相似的图形,它们有什么特征?
问题2 如图所示的五边形,把它放大为原来的 2 倍,即新图与原图的相似比为 2. 应该怎样做?你能说出画相似图形的一种方法吗?
一、创设情境,引入新课
问题3 观察下图,图中有多边形相似吗?如果有,那么这种相似什么共同的特征?
位似图形的概念:每幅图的两个多边形不仅是相似图形,而且是每组对应点连线相交于一点,像这样的两个图形叫做位似图形.这个点叫做位似中心.这时我们说这两个图形关于这点位似.
二、合作交流,探究新知
问题4 你能利用位似,把一个图形放大或缩小吗?请把图中的四边形 ABCD 缩小到原来的 1/2.
分析:把原图形缩小到原来的 1/2,也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2 .
二、合作交流,探究新知
作法一:(1)在四边形 ABCD 外任取一点O;
(2)过点 O 分别作射线OA,OB,OC,OD;
(3)分别在射线 OA,OB,OC,OD上取点A′、B′、C′、D′,
使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
追问:你还有其它方法作出符合条件的图形吗?
二、合作交流,探究新知
作法二:(1)在四边形 ABCD 外任取一点 O;
(2)过点 O 分别作射线 OA, OB, OC,OD;
(3)分别在射线 OA, OB, OC, OD 的反向延长线上取点A′、B′、C′、D′,使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
二、合作交流,探究新知
作法三:(1)在四边形 ABCD 内任取一点O;
(2)过点 O 分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,
使得 ;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′.
二、合作交流,探究新知
二、合作交流,探究新知
问题6 至此,我们已经学移、轴对称、旋转和位似等图形的变化方式.在下面的图案中,你能找出平移、轴对称、旋转和位似这些变换吗?
二、合作交流,探究新知
追问:还可以得到其它图形吗?自己试一试.
三、运用新知
三、运用新知
1. 下列说法正确的是( )
A. 相似的两个五边形一定是位似图形
B. 两个大小不同的正三角形一定是位似图形
C. 两个位似图形一定是相似图形
D. 所有的正方形都是位似图形
解析:位似图形是相似图形的特例,相似图形不一定是位似图形,故答案应选择 C.
C
四、巩固新知
2. 两个位似多边形一对对应顶点到位似中心的距离比为1∶2,且它们面积和为80,则较小的多边形的面积是( )
A. 16 B. 32 C. 48 D. 64
解析:位似图形必定相似,具备相似形的性质,其相似比等于一对对应顶点到位似中心的距离比.相似比为1∶2,则面积比为1∶4,由面积和为80,得到它们的面积分别为16,64. 故答案应选择 A.
A
四、巩固新知
四、巩固新知
3. 如图, △ABC 三个顶点坐标分别为A(2 , 3), B(2, 1), C(6, 2).
(1)将△ABC 向左平移三个单位得到△A1B1C1 ,写出A1、B1、C1三点的坐标;
(2)写出△ABC 关于 x 轴对称的△A2B2C2 三个顶点A2、B2、C2的坐标;
(3)将△ABC 绕点 O 旋转180°得到△A3B3C3 ,写出A3、B3、 C3三点的坐标.
4. 利用位似的方法把下图缩小到原来的一半,要求所作的图形在原图内部.
答案:
四、巩固新知
回顾本节课的学习,回答下列问题:
1. 什么样的图形叫做位似图形?位似中心是什么?
2. 利用位似如何给一个多边形放大或缩小?
3. 在直角坐标系中,如何研究两个位似图形对应点的坐标之间的关系?
4. 我们以前学过的平移、对称、旋转变换,它们的特点是什么?位似变换的特点是什么?
五、归纳小结
再 见
