第6章 平面图形的认识(一) 单元精选精练卷(含解析)
文档属性
| 名称 | 第6章 平面图形的认识(一) 单元精选精练卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 900.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 17:24:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第6章 平面图形的认识(一) 单元精选精练卷 2023-2024学年苏科版(2012)七年级数学上册
一、单选题
1.下列说法正确的是( )
A.直线比射线长 B.线段的长度就是,两点之间的距离
C.延长射线至点 D.两点之间,直线最短
2.下面说法与几何图形相符的是( )
A.点在直线上 B.直线与都经过点
C.可以表示成 D.直线和直线表示同一条直线
3.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长2017厘米的线段,则线段盖住的整点共有( )个
A.2018或2019 B.2017或2018 C.2016或2017 D.2015或2016
4.如图,已知线段,,,求作一条线段,使它等于.作法:①画射线;②在射线上顺次截取,;④在线段上截取.那么所求作的线段是( )
A. B. C. D.
5.如图,下列表示角的方法正确的是( )
A. B. C. D.
6.如图,在灯塔O处观测到轮船A位于北偏西的方向,同时观测到轮船C在东南方向,轮船B在的反向延长线的方向上,则的大小为( )
A. B. C. D.
7.如图,将直角三角尺与的直角顶点叠放在一起,若,则的度数为( )
A. B. C. D.
8.如图,点O在直线上,,若,则的补角的大小为( )
A. B. C. D.
9.如图,一把张开的剪刀,给我们两条直线相交的形象,则图中之间的关系不一定成立的是( )
A. B. C. D.
10.如图,在同一平面内,经过直线m外一点O的四条直线中,与直线m相交的直线最少有( )
A.1条 B.2条 C.3条 D.4条
11.如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m平行,请借助直尺判断该线段是( )
A.a B.b C.c D.d
12.如图,,点在上,,则的度数是( )
A. B. C. D.
13.如图,点在直线上,点,在直线上,设,且无论取何值,均有,则下列说法正确的是( )
A.点到直线的距离是的长度 B.点到直线的距离是的长度
C.点到直线的距离是的长度 D.点到直线的距离是的长度
二、填空题
14.已知线段,点在直线上,,点是线段的中点,则线段 .
15.将图中的角用不同的方法表示出来,并填写下表:
万杰朝阳学校上午第二节课的下课时间是9:40,此时时针与分针的夹角是 .
16.如图,直线与相交于点,且,则的度数为 .
17.如图是利用直尺移动三角板过直线外一点作直线的平行线的方法,小明经过多次实践后发现只能作一条平行线,这反映了 .
18.在中,、过作,垂足为,已知,,,点到的距离为 ,这个长度是 .
三、解答题
19.如图,点在线段上,点是线段的中点,.
(1)尺规作图:延长线段,并在延长线上作一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求线段的长度.
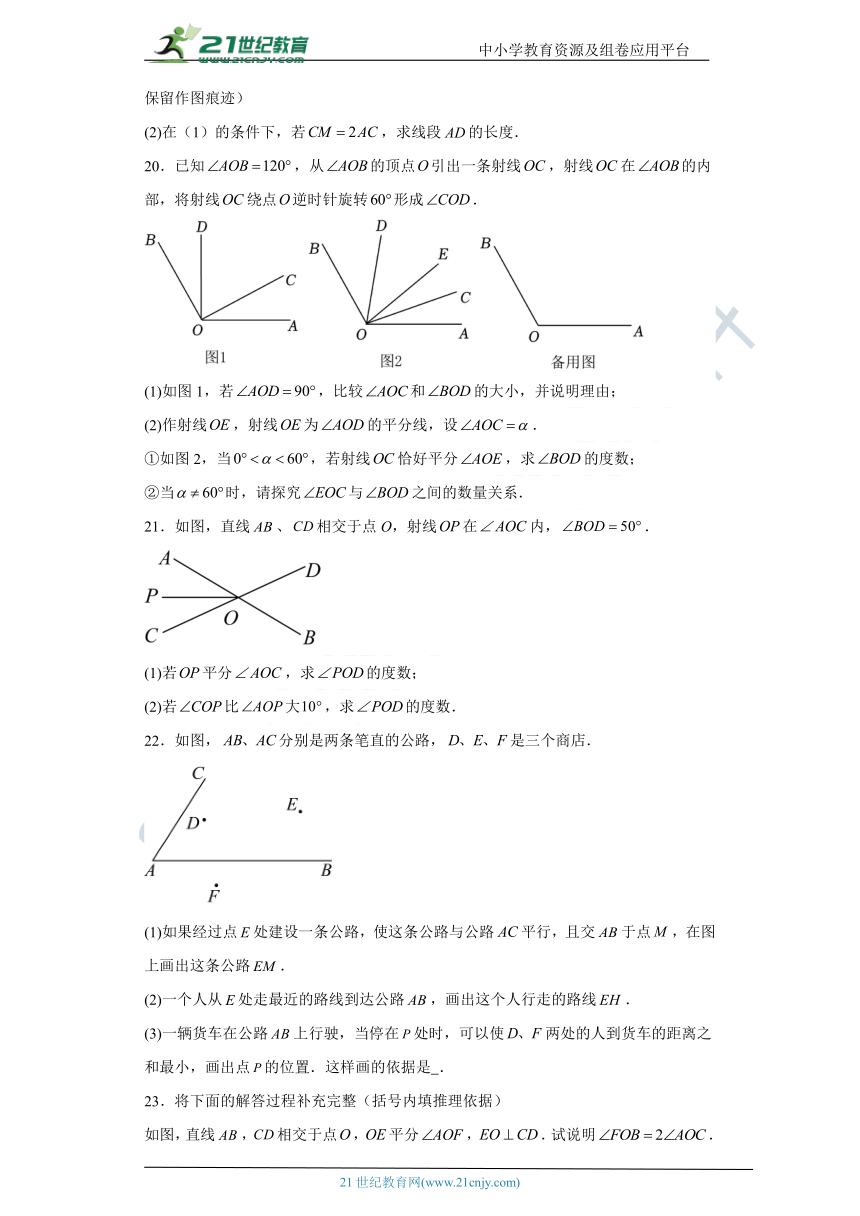
20.已知,从的顶点引出一条射线,射线在的内部,将射线绕点逆时针旋转形成.
(1)如图1,若,比较和的大小,并说明理由;
(2)作射线,射线为的平分线,设.
①如图2,当,若射线恰好平分,求的度数;
②当时,请探究与之间的数量关系.
21.如图,直线、相交于点O,射线在内,.
(1)若平分,求的度数;
(2)若比大,求的度数.
22.如图,分别是两条笔直的公路,是三个商店.
(1)如果经过点处建设一条公路,使这条公路与公路平行,且交于点,在图上画出这条公路.
(2)一个人从处走最近的路线到达公路,画出这个人行走的路线.
(3)一辆货车在公路上行驶,当停在处时,可以使两处的人到货车的距离之和最小,画出点的位置.这样画的依据是 .
23.将下面的解答过程补充完整(括号内填推理依据)
如图,直线,相交于点,平分,.试说明.
解:因为平分,所以______,
因为,所以,
所以,,
所以________,(________)
因为直线,相交于点,所以,(______)
所以.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据直线,射线,线段的相关概念逐项判断即可.
【详解】解:A、射线,直线都是可以无限延长的,无法测量长度,原说法错误;
B、线段的长度就是,两点之间的距离,正确;
C、射线本身就是向一端无限延伸,原说法错误;
D、两点之间,线段最短,原说法错误;
故选:B.
【点睛】本题考查了两点间的距离的定义,直线、射线、线段,直线和线段的性质,是基础题,熟记相关概念与性质是解题的关键.
2.B
【分析】利用点和直线的关系,结合图形,对选项一一分析,选出正确答案.
【详解】解:A、点不在直线上,故错误,不合题意;
B、直线与都经过点,故正确,符合题意;
C、不能表示成,故原说法错误,不合题意;
D、直线和直线表示同一条直线,故原说法错误,不合题意;
故选:B.
【点睛】本题考查了点和直线的关系,直线的性质,注意仔细观察图形.
3.B
【分析】分线段的端点与整点重合和不重合两种情况考虑,重合时盖住的整点是线段的长度+1,不重合时盖住的整点是线段的长度,由此即可得出结论.
【详解】解:若线段的端点恰好与整点重合,则2017厘米长的线段盖住个整点,个整点,
若线段的端点不与整点重合,则2017厘米的线段盖住2017个整点.
∴2017厘米的线段盖住2017或2018个整点.
故选:B.
【点睛】本题考查了数轴,解题的关键是找出长度为n(n为正整数)的线段盖住n或个整点.本题属于基础题,难度不大,解决该题型题目时,分端点是否与整点重合两种情况来考虑是关键.
4.C
【分析】根据线段的和差即可得.
【详解】解:,,,
,
故选:C.
【点睛】本题考查了作线段,熟练掌握线段的和差是解题关键.
5.C
【分析】根据角的定义进行判断即可得.
【详解】解:根据图得,表示角的方法正确的是,
故选:C.
【点睛】本题考查了角,解题的关键是掌握角的定义.
6.B
【分析】根据对顶角相等,求出轮船B在灯塔O的南偏东的方向,然后减去即可.
【详解】解:根据对顶角相等,得:
轮船B在灯塔O的南偏东的方向,
由题意得:,
故选:B.
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
7.D
【分析】因为是和的重叠部分,因此由
即可求出的度数.
【详解】,
,
即,
即,
.
故选:D.
【点睛】本题主要考查了角的和差的计算.熟练掌握角的和差的计算,发现是和的重叠部分是解题的关键.
8.B
【分析】根据垂直定义可得,从而利用角的和差关系可得,然后利用同角(等角)的补角相等,即可解答.
【详解】解:∵,
∴,
∵,
∴,
∵和互为邻补角,
∴的补角的大小为,
故选:B.
【点睛】本题考查了垂线以及余角和补角,根据题目的已知条件并结合图形进行分析是解题的关键.
9.B
【分析】根据邻补角的定义和对顶角的性质分别判断即可.
【详解】解:由图可知:
和为邻补角,和为邻补角,和为对顶角,
∴,,,
∴选项A,C,D成立,选项B不一定成立,
故选:B.
【点睛】本题考查了邻补角和对顶角,解题的关键是掌握相应的定义和性质.
10.C
【分析】根据经过直线外一点有且只有一条直线和已知直线平行进行求解即可.
【详解】解:根据经过直线外一点有且只有一条直线和已知直线平行,得出过点的条直线中至多只有一条直线与直线平行
即与直线相交的直线至少有条.
故选:C.
【点睛】本题考查了平行线的性质,熟练掌握经过直线外一点有且只有一条直线和已知直线平行性质是解题的关键.
11.C
【分析】利用直尺画出遮挡的部分即可得出结论.
【详解】解:利用直尺画出图形如下:
可以看出线段与平行.
故选:C.
【点睛】本题主要考查了平行线,熟记平行线的画法是解题的关键.
12.A
【分析】延长交于点,由垂线的定义可得,由对顶角相等可得,最后进行计算即可求出的度数.
【详解】解:如图,延长交于点,
,
,
,
,
,
故选:A.
【点睛】本题主要考查了垂线的定义、对顶角相等、求一个角的余角,熟练掌握垂线的定义、对顶角相等,添加适当的辅助线,是解题的关键.
13.B
【分析】根据点到直线的距离,垂线段最短即可求解.
【详解】解:∵,且无论取何值,均有,
∴点到直线的距离是的长度,
故选:B.
【点睛】本题考查了点到直线的距离,垂线段最短,熟练掌握点到直线的距离,垂线段最短是解题的关键.
14.9或6/6或9
【分析】分两种情况,可分别画出图形,结合线段中点定义求解即可.
【详解】解:根据题意,分两种情况:
①如图,
∵,,
∴,
∵点是线段的中点,
∴;
②如图,
∵,,
∴,
∵点是线段的中点,
∴,
综上,9或6,
故答案为:9或6.
【点睛】本题考查线段中点有关的计算,分类讨论求解是解答的关键.
15. 50
【分析】根据角的表示方法结合图中角的位置可得到①-⑤;根据钟表上,一大格是求解⑥即可.
【详解】解:根据图形,填表如下:
万杰朝阳学校上午第二节课的下课时间是9:40,此时时针与分针的夹角是,
故答案为:,,,,,50.
【点睛】本题考查角的表示、钟面角,熟知角的表示方法和钟面上一大格是是解答的关键.
16./度
【分析】根据对顶角相等,结合已知条件,进而根据邻补角的定义即可求解.
【详解】解:,且,
,
,
.
故答案为:.
【点睛】本题考查了对顶角相等,邻补角,熟练掌握对顶角相等是解题的关键.
17.过直线外一点有且只有一条直线与已知直线平行
【分析】根据平行公理可得答案.
【详解】解:由图可得,过直线外一点,能且只能画出一条平行线,
这反映了:过直线外一点有且只有一条直线与已知直线平行.
故答案为:过直线外一点有且只有一条直线与已知直线平行.
【点睛】本题考查平行公里,熟练掌握平行线的判定与性质是解答本题的关键.
18. 线段的长度 12
【分析】根据点到直线的距离为过该点到直线的垂线段的距离,进行判断计算即可.
【详解】解:∵,
∴点到的距离为线段的长度,
∵,
∴这个长度是;
故答案为:线段的长度,12.
【点睛】本题考查点到直线的距离.熟练掌握点到直线的距离为点到直线的垂线段的长度,是解题的关键.
19.(1)见解析
(2)7
【分析】(1)延长线段,在延长线上截取即可;
(2)根据中点的定义求出,再根据求出,结合即可求解.
【详解】(1)解:,
若,则,
以点B为圆心,长为半径作弧,与线段的延长线的交点即为点D,如下图所示:
;
(2)解:点是线段的中点,,
,
,
,
由(1)知,
.
【点睛】本题考查尺规作图——作一线段等于已知线段,中点的定义,线段的和差关系等,难度一般,解题的关键是熟练掌握上述知识点.
20.(1),理由见解析
(2)①②
【分析】(1)根据,,即可确定两个角的大小;
(2)①根据角平分线的定义可得,,根据列方程,求出的值,再根据计算即可;
②分两种情况:当时,当时,分别根据角平分线的定义,角的和差计算即可.
【详解】(1)解:,理由如下:
,,
,
又
,
;
(2)①恰好平分,
,
,
为的平分线,
,
,
,
,
,
;
②分情况讨论:
当时,
,
,为的平分线,
,
,
;
当时,
,
,为的平分线,
,
,
;
综上所述,.
【点睛】本题考查了角平分线的定义,角的计算,熟练掌握角平分线的定义是解题的关键.
21.(1)
(2)
【分析】(1)根据对顶角性质得到,根据角平分线定义得到,根据邻补角性质得到,即得;
(2)根据,,得到,根据,得到.
【详解】(1)∵,与为对顶角,
∴,
∴,
∵平分,
∴,
∴
(2)由(1)知:, ,
又∵比大,
∴,,
∴,
∴.
【点睛】本题主要考查了角平分线,邻补角等,解决问题的关键是熟练掌握角平分线定义,邻补角定义.
22.(1)图见解析;
(2)图见解析;
(3)图见解析,两点之间线段最短;
【分析】(1)根据尺规作平行线的方法即可解答;
(2)根据尺规作垂线的方法即可解答;
(3)根据两点之间线段最短即可解答.
【详解】(1)解:如图所示即为所求,
(2)解:如图所示即为所求,
(3)解:如图所示点即为所求
依据是:两点之间线段最短;
故答案为:两点之间线段最短.
【点睛】本题考查了尺规作平行线的方法,两点之间线段最短,尺规作垂线的方法,掌握尺规作图法是解题的关键.
23.,90,,,等角的余角相等,对顶角相等
【分析】根据角平分线的定义、垂直的定义、对顶角相等、等角的余角相等,分析解答即可.
【详解】解:因为平分,所以,
因为,所以,
所以,,
所以,(等角的余角相等)
因为直线,相交于点,所以,(对顶角相等)
所以.
【点睛】本题主要考查了对顶角、角平分线、垂线、余角等知识,熟练掌握对顶角相等、角平分线的定义是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第6章 平面图形的认识(一) 单元精选精练卷 2023-2024学年苏科版(2012)七年级数学上册
一、单选题
1.下列说法正确的是( )
A.直线比射线长 B.线段的长度就是,两点之间的距离
C.延长射线至点 D.两点之间,直线最短
2.下面说法与几何图形相符的是( )
A.点在直线上 B.直线与都经过点
C.可以表示成 D.直线和直线表示同一条直线
3.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长2017厘米的线段,则线段盖住的整点共有( )个
A.2018或2019 B.2017或2018 C.2016或2017 D.2015或2016
4.如图,已知线段,,,求作一条线段,使它等于.作法:①画射线;②在射线上顺次截取,;④在线段上截取.那么所求作的线段是( )
A. B. C. D.
5.如图,下列表示角的方法正确的是( )
A. B. C. D.
6.如图,在灯塔O处观测到轮船A位于北偏西的方向,同时观测到轮船C在东南方向,轮船B在的反向延长线的方向上,则的大小为( )
A. B. C. D.
7.如图,将直角三角尺与的直角顶点叠放在一起,若,则的度数为( )
A. B. C. D.
8.如图,点O在直线上,,若,则的补角的大小为( )
A. B. C. D.
9.如图,一把张开的剪刀,给我们两条直线相交的形象,则图中之间的关系不一定成立的是( )
A. B. C. D.
10.如图,在同一平面内,经过直线m外一点O的四条直线中,与直线m相交的直线最少有( )
A.1条 B.2条 C.3条 D.4条
11.如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m平行,请借助直尺判断该线段是( )
A.a B.b C.c D.d
12.如图,,点在上,,则的度数是( )
A. B. C. D.
13.如图,点在直线上,点,在直线上,设,且无论取何值,均有,则下列说法正确的是( )
A.点到直线的距离是的长度 B.点到直线的距离是的长度
C.点到直线的距离是的长度 D.点到直线的距离是的长度
二、填空题
14.已知线段,点在直线上,,点是线段的中点,则线段 .
15.将图中的角用不同的方法表示出来,并填写下表:
万杰朝阳学校上午第二节课的下课时间是9:40,此时时针与分针的夹角是 .
16.如图,直线与相交于点,且,则的度数为 .
17.如图是利用直尺移动三角板过直线外一点作直线的平行线的方法,小明经过多次实践后发现只能作一条平行线,这反映了 .
18.在中,、过作,垂足为,已知,,,点到的距离为 ,这个长度是 .
三、解答题
19.如图,点在线段上,点是线段的中点,.
(1)尺规作图:延长线段,并在延长线上作一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求线段的长度.
20.已知,从的顶点引出一条射线,射线在的内部,将射线绕点逆时针旋转形成.
(1)如图1,若,比较和的大小,并说明理由;
(2)作射线,射线为的平分线,设.
①如图2,当,若射线恰好平分,求的度数;
②当时,请探究与之间的数量关系.
21.如图,直线、相交于点O,射线在内,.
(1)若平分,求的度数;
(2)若比大,求的度数.
22.如图,分别是两条笔直的公路,是三个商店.
(1)如果经过点处建设一条公路,使这条公路与公路平行,且交于点,在图上画出这条公路.
(2)一个人从处走最近的路线到达公路,画出这个人行走的路线.
(3)一辆货车在公路上行驶,当停在处时,可以使两处的人到货车的距离之和最小,画出点的位置.这样画的依据是 .
23.将下面的解答过程补充完整(括号内填推理依据)
如图,直线,相交于点,平分,.试说明.
解:因为平分,所以______,
因为,所以,
所以,,
所以________,(________)
因为直线,相交于点,所以,(______)
所以.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据直线,射线,线段的相关概念逐项判断即可.
【详解】解:A、射线,直线都是可以无限延长的,无法测量长度,原说法错误;
B、线段的长度就是,两点之间的距离,正确;
C、射线本身就是向一端无限延伸,原说法错误;
D、两点之间,线段最短,原说法错误;
故选:B.
【点睛】本题考查了两点间的距离的定义,直线、射线、线段,直线和线段的性质,是基础题,熟记相关概念与性质是解题的关键.
2.B
【分析】利用点和直线的关系,结合图形,对选项一一分析,选出正确答案.
【详解】解:A、点不在直线上,故错误,不合题意;
B、直线与都经过点,故正确,符合题意;
C、不能表示成,故原说法错误,不合题意;
D、直线和直线表示同一条直线,故原说法错误,不合题意;
故选:B.
【点睛】本题考查了点和直线的关系,直线的性质,注意仔细观察图形.
3.B
【分析】分线段的端点与整点重合和不重合两种情况考虑,重合时盖住的整点是线段的长度+1,不重合时盖住的整点是线段的长度,由此即可得出结论.
【详解】解:若线段的端点恰好与整点重合,则2017厘米长的线段盖住个整点,个整点,
若线段的端点不与整点重合,则2017厘米的线段盖住2017个整点.
∴2017厘米的线段盖住2017或2018个整点.
故选:B.
【点睛】本题考查了数轴,解题的关键是找出长度为n(n为正整数)的线段盖住n或个整点.本题属于基础题,难度不大,解决该题型题目时,分端点是否与整点重合两种情况来考虑是关键.
4.C
【分析】根据线段的和差即可得.
【详解】解:,,,
,
故选:C.
【点睛】本题考查了作线段,熟练掌握线段的和差是解题关键.
5.C
【分析】根据角的定义进行判断即可得.
【详解】解:根据图得,表示角的方法正确的是,
故选:C.
【点睛】本题考查了角,解题的关键是掌握角的定义.
6.B
【分析】根据对顶角相等,求出轮船B在灯塔O的南偏东的方向,然后减去即可.
【详解】解:根据对顶角相等,得:
轮船B在灯塔O的南偏东的方向,
由题意得:,
故选:B.
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
7.D
【分析】因为是和的重叠部分,因此由
即可求出的度数.
【详解】,
,
即,
即,
.
故选:D.
【点睛】本题主要考查了角的和差的计算.熟练掌握角的和差的计算,发现是和的重叠部分是解题的关键.
8.B
【分析】根据垂直定义可得,从而利用角的和差关系可得,然后利用同角(等角)的补角相等,即可解答.
【详解】解:∵,
∴,
∵,
∴,
∵和互为邻补角,
∴的补角的大小为,
故选:B.
【点睛】本题考查了垂线以及余角和补角,根据题目的已知条件并结合图形进行分析是解题的关键.
9.B
【分析】根据邻补角的定义和对顶角的性质分别判断即可.
【详解】解:由图可知:
和为邻补角,和为邻补角,和为对顶角,
∴,,,
∴选项A,C,D成立,选项B不一定成立,
故选:B.
【点睛】本题考查了邻补角和对顶角,解题的关键是掌握相应的定义和性质.
10.C
【分析】根据经过直线外一点有且只有一条直线和已知直线平行进行求解即可.
【详解】解:根据经过直线外一点有且只有一条直线和已知直线平行,得出过点的条直线中至多只有一条直线与直线平行
即与直线相交的直线至少有条.
故选:C.
【点睛】本题考查了平行线的性质,熟练掌握经过直线外一点有且只有一条直线和已知直线平行性质是解题的关键.
11.C
【分析】利用直尺画出遮挡的部分即可得出结论.
【详解】解:利用直尺画出图形如下:
可以看出线段与平行.
故选:C.
【点睛】本题主要考查了平行线,熟记平行线的画法是解题的关键.
12.A
【分析】延长交于点,由垂线的定义可得,由对顶角相等可得,最后进行计算即可求出的度数.
【详解】解:如图,延长交于点,
,
,
,
,
,
故选:A.
【点睛】本题主要考查了垂线的定义、对顶角相等、求一个角的余角,熟练掌握垂线的定义、对顶角相等,添加适当的辅助线,是解题的关键.
13.B
【分析】根据点到直线的距离,垂线段最短即可求解.
【详解】解:∵,且无论取何值,均有,
∴点到直线的距离是的长度,
故选:B.
【点睛】本题考查了点到直线的距离,垂线段最短,熟练掌握点到直线的距离,垂线段最短是解题的关键.
14.9或6/6或9
【分析】分两种情况,可分别画出图形,结合线段中点定义求解即可.
【详解】解:根据题意,分两种情况:
①如图,
∵,,
∴,
∵点是线段的中点,
∴;
②如图,
∵,,
∴,
∵点是线段的中点,
∴,
综上,9或6,
故答案为:9或6.
【点睛】本题考查线段中点有关的计算,分类讨论求解是解答的关键.
15. 50
【分析】根据角的表示方法结合图中角的位置可得到①-⑤;根据钟表上,一大格是求解⑥即可.
【详解】解:根据图形,填表如下:
万杰朝阳学校上午第二节课的下课时间是9:40,此时时针与分针的夹角是,
故答案为:,,,,,50.
【点睛】本题考查角的表示、钟面角,熟知角的表示方法和钟面上一大格是是解答的关键.
16./度
【分析】根据对顶角相等,结合已知条件,进而根据邻补角的定义即可求解.
【详解】解:,且,
,
,
.
故答案为:.
【点睛】本题考查了对顶角相等,邻补角,熟练掌握对顶角相等是解题的关键.
17.过直线外一点有且只有一条直线与已知直线平行
【分析】根据平行公理可得答案.
【详解】解:由图可得,过直线外一点,能且只能画出一条平行线,
这反映了:过直线外一点有且只有一条直线与已知直线平行.
故答案为:过直线外一点有且只有一条直线与已知直线平行.
【点睛】本题考查平行公里,熟练掌握平行线的判定与性质是解答本题的关键.
18. 线段的长度 12
【分析】根据点到直线的距离为过该点到直线的垂线段的距离,进行判断计算即可.
【详解】解:∵,
∴点到的距离为线段的长度,
∵,
∴这个长度是;
故答案为:线段的长度,12.
【点睛】本题考查点到直线的距离.熟练掌握点到直线的距离为点到直线的垂线段的长度,是解题的关键.
19.(1)见解析
(2)7
【分析】(1)延长线段,在延长线上截取即可;
(2)根据中点的定义求出,再根据求出,结合即可求解.
【详解】(1)解:,
若,则,
以点B为圆心,长为半径作弧,与线段的延长线的交点即为点D,如下图所示:
;
(2)解:点是线段的中点,,
,
,
,
由(1)知,
.
【点睛】本题考查尺规作图——作一线段等于已知线段,中点的定义,线段的和差关系等,难度一般,解题的关键是熟练掌握上述知识点.
20.(1),理由见解析
(2)①②
【分析】(1)根据,,即可确定两个角的大小;
(2)①根据角平分线的定义可得,,根据列方程,求出的值,再根据计算即可;
②分两种情况:当时,当时,分别根据角平分线的定义,角的和差计算即可.
【详解】(1)解:,理由如下:
,,
,
又
,
;
(2)①恰好平分,
,
,
为的平分线,
,
,
,
,
,
;
②分情况讨论:
当时,
,
,为的平分线,
,
,
;
当时,
,
,为的平分线,
,
,
;
综上所述,.
【点睛】本题考查了角平分线的定义,角的计算,熟练掌握角平分线的定义是解题的关键.
21.(1)
(2)
【分析】(1)根据对顶角性质得到,根据角平分线定义得到,根据邻补角性质得到,即得;
(2)根据,,得到,根据,得到.
【详解】(1)∵,与为对顶角,
∴,
∴,
∵平分,
∴,
∴
(2)由(1)知:, ,
又∵比大,
∴,,
∴,
∴.
【点睛】本题主要考查了角平分线,邻补角等,解决问题的关键是熟练掌握角平分线定义,邻补角定义.
22.(1)图见解析;
(2)图见解析;
(3)图见解析,两点之间线段最短;
【分析】(1)根据尺规作平行线的方法即可解答;
(2)根据尺规作垂线的方法即可解答;
(3)根据两点之间线段最短即可解答.
【详解】(1)解:如图所示即为所求,
(2)解:如图所示即为所求,
(3)解:如图所示点即为所求
依据是:两点之间线段最短;
故答案为:两点之间线段最短.
【点睛】本题考查了尺规作平行线的方法,两点之间线段最短,尺规作垂线的方法,掌握尺规作图法是解题的关键.
23.,90,,,等角的余角相等,对顶角相等
【分析】根据角平分线的定义、垂直的定义、对顶角相等、等角的余角相等,分析解答即可.
【详解】解:因为平分,所以,
因为,所以,
所以,,
所以,(等角的余角相等)
因为直线,相交于点,所以,(对顶角相等)
所以.
【点睛】本题主要考查了对顶角、角平分线、垂线、余角等知识,熟练掌握对顶角相等、角平分线的定义是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
