角平分线的性质
图片预览


文档简介
(共32张PPT)
学习数学并不难,
学习数学就像交朋友一样,
朋友是越交越熟的,
天天见面,
朋友之间就亲密无间了。
让我们一起扬帆启航吧!
角平分线的性质
复习提问
2、角平分线的概念
1、点到直线距离的意义。
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离。
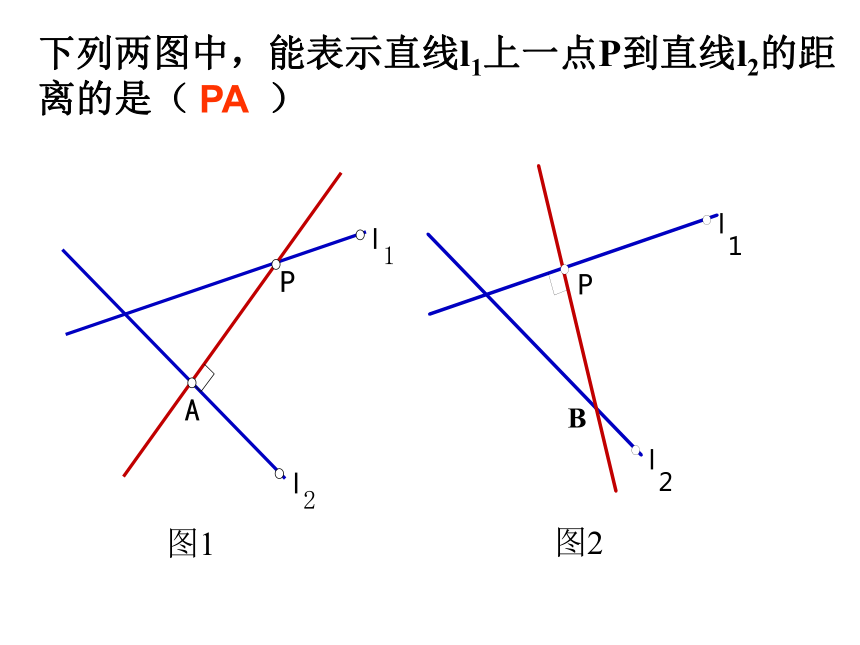
下列两图中,能表示直线l1上一点P到直线l2的距离的是( )
图1
图2
B
P
A
l
1
l
2
PA
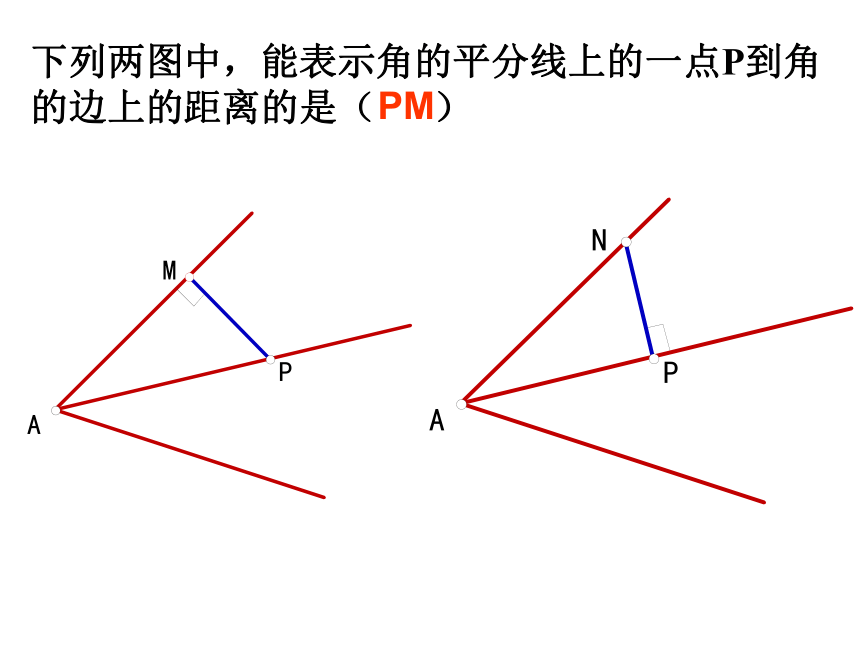
下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
PM
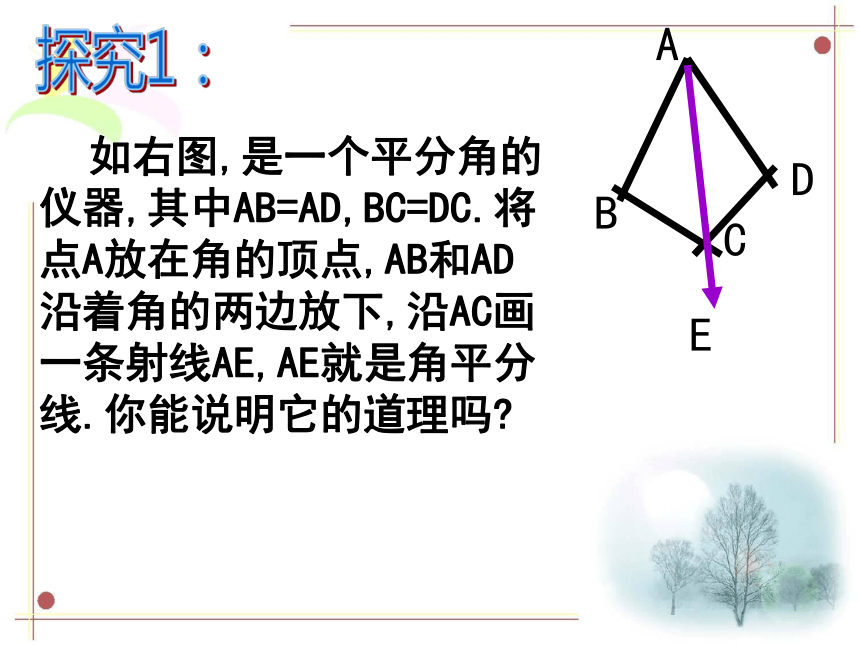
如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗
A
C
D
B
E
A
B
M
N
C
.
O
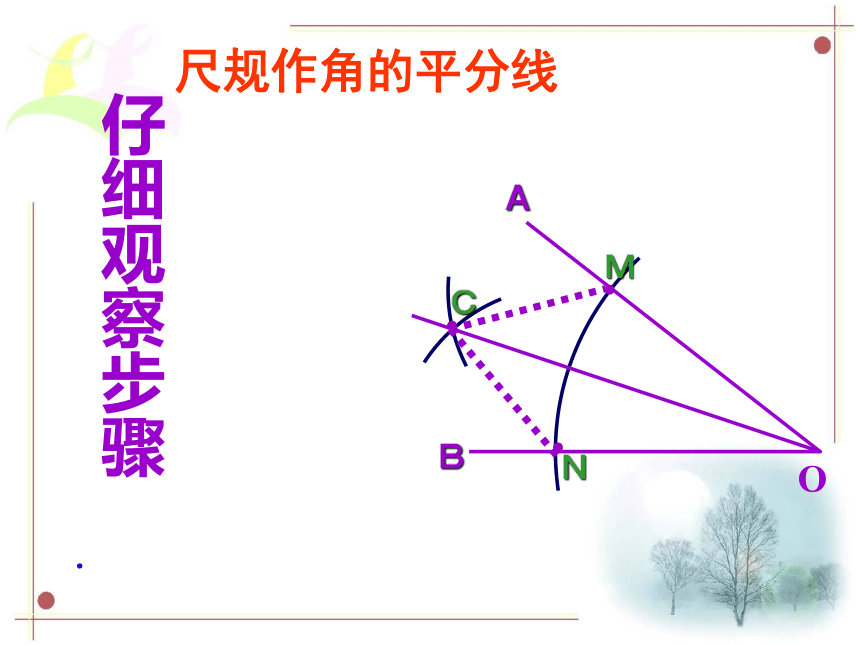
仔细观察步骤
尺规作角的平分线
A
B
M
N
C
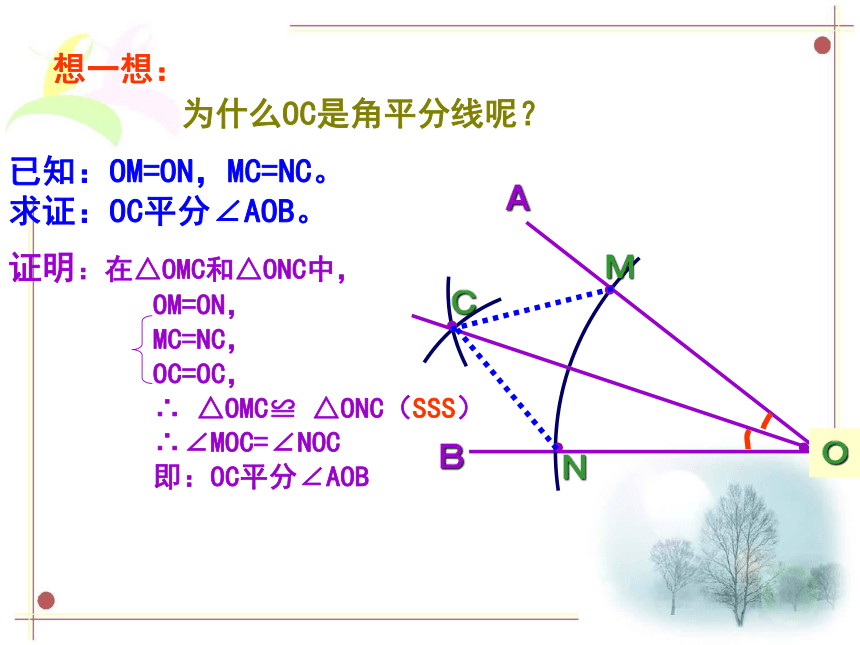
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
O
A
O
E
B
C
P
D
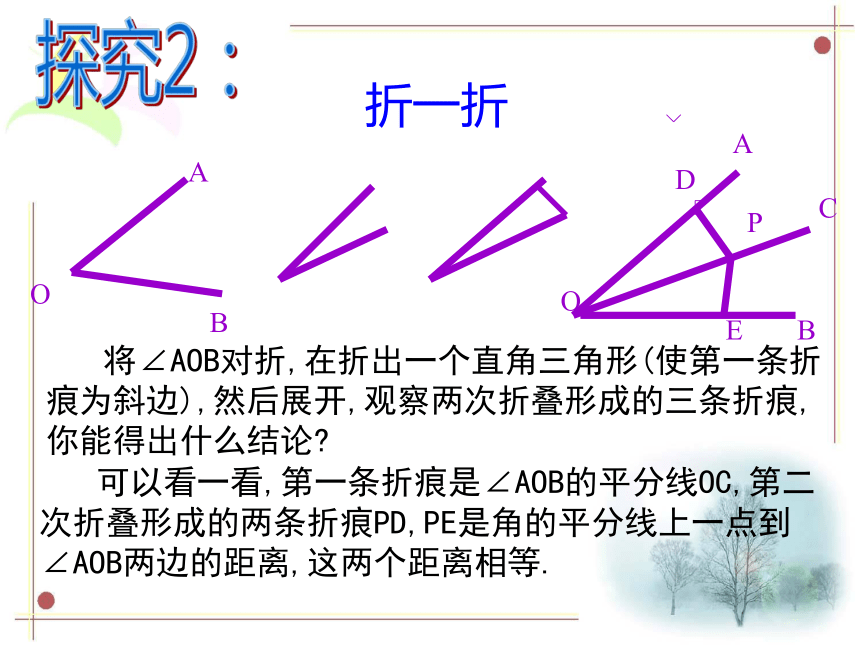
将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论
可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.
折一折
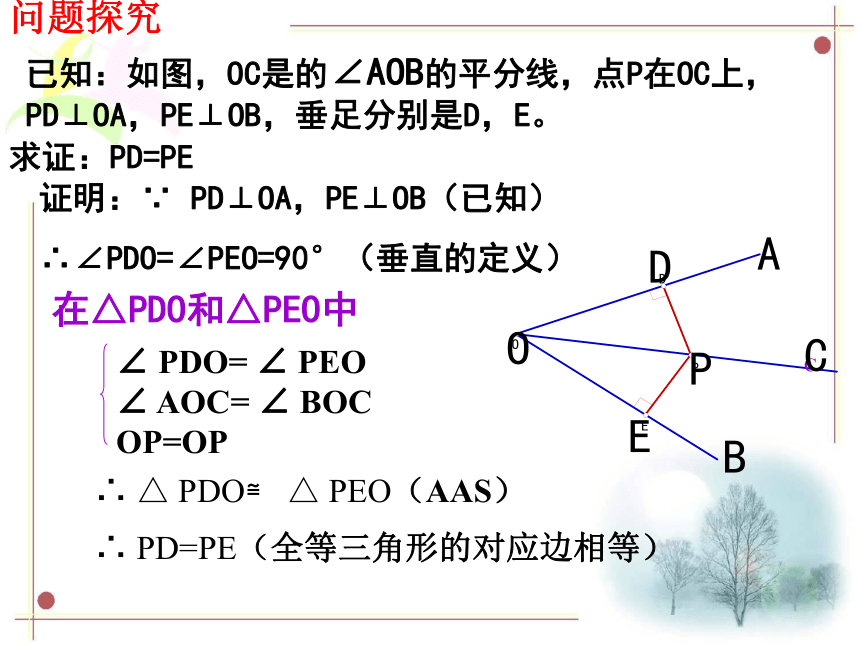
已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
C
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
问题探究
A
B
O
D
E
P
C
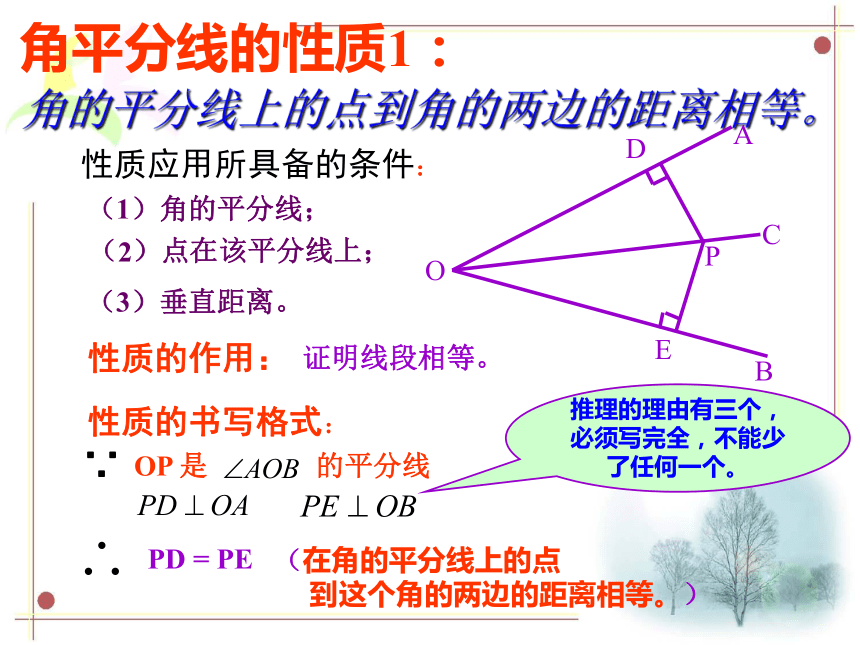
角平分线的性质1:
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
性质应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
性质的作用:
证明线段相等。
性质的书写格式:
OP 是 的平分线
\
PD = PE
(在角的平分线上的点
到这个角的两边的距离相等。)
∵
推理的理由有三个,必须写完全,不能少了任何一个。
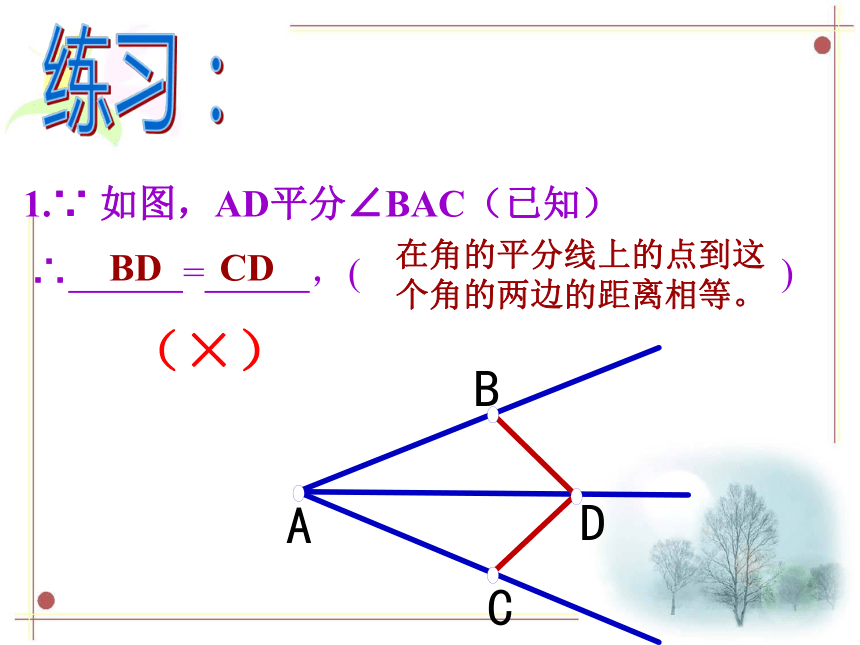
1.∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
2.∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
3.∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,要在S区建一个集贸市场,使它到公路、河流的距离相等,并且离公路与河流交叉处300米,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000 )?
北
比例尺1:20000
S
△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
连接OP并延长OP
即点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
性质 2
B
A
D
O
P
E
∵
∴OP平分∠AOB
性质 2的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
性质 1 在角的平分线上的点到这个角的两边的距离相等。
性质 2 到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
∴ _________ ____
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
AD平分∠BAC
A
N
B
C
P
M
知识应用
1.如图,△ABC的角的平分线BM,
CN相交于点P.求证:点P到三边AB,BC,
CA的距离相等.
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
例:已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 垂直AB于D,PE垂直BC于E,PF垂直CA于F
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
∵BM是△ABC的角平分线,点P在BM上
2..直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有: ( )
A.一处 B. 两处
C.三处 D.四处
2 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
3.如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
6cm
课堂练习
如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且CD:DB=1:2,则点D到AB的距离为_________。
已知:如图, ∠ C= ∠ D=90° , BC=BD 。
求证:(1)∠BAC= ∠BAD
(2) AC=AD
A
D
C
B
5.如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。
求证:MD=ME。
AD是∠BAC的平分线,DE⊥AB于E点,DF⊥AC于F点,且DB=DC
求证: ∠EBD= ∠FCD 。
E
A
c
F
B
D
3.如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。
求证: ∠BDP= ∠CDP
小 结:
3 角的平分线的性质定理1,定理2是证明角相等,线段相等的新途径。定理1多用于证明线段相等,定理2多用于证明角相等或点在角平分线上。
1 在角的平分线上的点到这个角的两边的距离相等。
2 到一个角的两边距离相等的点,在这个角的平分线上。
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
学习数学并不难,
学习数学就像交朋友一样,
朋友是越交越熟的,
天天见面,
朋友之间就亲密无间了。
让我们一起扬帆启航吧!
角平分线的性质
复习提问
2、角平分线的概念
1、点到直线距离的意义。
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离。
下列两图中,能表示直线l1上一点P到直线l2的距离的是( )
图1
图2
B
P
A
l
1
l
2
PA
下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
PM
如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗
A
C
D
B
E
A
B
M
N
C
.
O
仔细观察步骤
尺规作角的平分线
A
B
M
N
C
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
O
A
O
E
B
C
P
D
将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论
可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.
折一折
已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
C
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
问题探究
A
B
O
D
E
P
C
角平分线的性质1:
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
性质应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
性质的作用:
证明线段相等。
性质的书写格式:
OP 是 的平分线
\
PD = PE
(在角的平分线上的点
到这个角的两边的距离相等。)
∵
推理的理由有三个,必须写完全,不能少了任何一个。
1.∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
2.∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
3.∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,要在S区建一个集贸市场,使它到公路、河流的距离相等,并且离公路与河流交叉处300米,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000 )?
北
比例尺1:20000
S
△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
连接OP并延长OP
即点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
性质 2
B
A
D
O
P
E
∵
∴OP平分∠AOB
性质 2的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
性质 1 在角的平分线上的点到这个角的两边的距离相等。
性质 2 到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
∴ _________ ____
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
AD平分∠BAC
A
N
B
C
P
M
知识应用
1.如图,△ABC的角的平分线BM,
CN相交于点P.求证:点P到三边AB,BC,
CA的距离相等.
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
例:已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 垂直AB于D,PE垂直BC于E,PF垂直CA于F
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
∵BM是△ABC的角平分线,点P在BM上
2..直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有: ( )
A.一处 B. 两处
C.三处 D.四处
2 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
3.如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么AE+DE= 。
6cm
课堂练习
如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且CD:DB=1:2,则点D到AB的距离为_________。
已知:如图, ∠ C= ∠ D=90° , BC=BD 。
求证:(1)∠BAC= ∠BAD
(2) AC=AD
A
D
C
B
5.如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。
求证:MD=ME。
AD是∠BAC的平分线,DE⊥AB于E点,DF⊥AC于F点,且DB=DC
求证: ∠EBD= ∠FCD 。
E
A
c
F
B
D
3.如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。
求证: ∠BDP= ∠CDP
小 结:
3 角的平分线的性质定理1,定理2是证明角相等,线段相等的新途径。定理1多用于证明线段相等,定理2多用于证明角相等或点在角平分线上。
1 在角的平分线上的点到这个角的两边的距离相等。
2 到一个角的两边距离相等的点,在这个角的平分线上。
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
