第4章等可能条件下的概率 单元精选精练卷(含解析)
文档属性
| 名称 | 第4章等可能条件下的概率 单元精选精练卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第4章等可能条件下的概率 单元精选精练卷 2023-2024学年苏科版(2012)九年级数学上册
一、单选题
1.如左图的天平架是平衡的,其中同一种物体的质量都相等,如右图,现将不同质量的一“○”和一个“”从通道的顶端同时放下,两个物体等可能的向左或向右落在下面的托盘中,此时两个托盘上物体的质量分别为和,则下列关系可能出现的是( )
A. B. C. D.
2.如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )
A.掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B.掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C.用计算器产生1和2两个随机整数,1代表正面,2代表反面
D.转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面
3.下列说法中正确的是( )
A.为了了解我国中学生的课外阅读情况,应采取全面调查方式
B.某彩票的中奖机会是,买100张一定会中奖
C.若a是实数,则是必然事件
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定
4.下列说法正确的是( )
A.小明投篮投中的概率是0.6,说明他投10次篮球一定能中6次
B.为了解全国中学生的节水意识,应采用普查的方式
C.为了解某校300名九年级学生的睡眠时间,从中抽取50名九年级学生进行调查,在这个事件中,样本容量是300
D.一个不透明口袋中装有3个红球2个白球,除颜色外都相同,从中任意摸出一个球,摸到红球的可能性比白球大
5.李明用6个球设计了一个摸球游戏,共有四种方案,肯定不能成功的是( )
A.摸到黄球、红球的概率均为
B.摸到黄球的概率是,摸到红球、白球的概率均为
C.摸到黄球、红球、白球的概率分别为、、
D.摸到黄球、红球、白球的概率都是
6.合肥市某校九年级(1)、(2)班共有2名女生和3名男生分别被评为“智慧之星”,要从这5位学生中随机抽取一男一女两位学生做获奖感言,女同学杨玲和男同学张军恰好来自同一班级,则他俩同时被抽中的概率为( )
A. B. C. D.
7.四张背面完全相同的卡片上分别写有1、2、3、4四个数字,把卡片背面朝上洗匀后,王明从这四张卡片中随机选两张,则王明选中的卡片中有偶数的概率是( )
A. B. C. D.
8.在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为( ).
A. B. C. D.
二、填空题
9.在一个不透明的袋子中装有个红球、个白球和个黑球,这些球除颜色外都相同.从中任意摸出个球,摸到 色的球的可能性最大.(填“红”、“白”或“黑”)
10.下列事件:
①如果、都是实数,那么;
②打开电视,正在播放新闻;
③抛掷一枚硬币,正面向上;
④张相同的小标签分别标有数字,从中任意抽取张,抽到号签.
属于确定事件的是 (填序号)
11.某航班每次约有200名乘客,一次飞行中飞机失事的概率,某保险公司为乘客提供保险,承诺飞机一旦失事,向每位乘客赔偿60万人民币.平均来说,保险公司应该至少向每位乘客收取 元保险费才不亏本.
12.在一个不透明的口袋中,装有3个球,它们分别写有数字1,2,3,这些球除上面数字外,其余都相同.先将这些球摇匀后,随机摸出一球,记下数字后,放回:再摇匀,再摸出一球.则摸出的两球的数字之和是4的概率是 .
三、解答题
13.求解下列问题:
(1)在1~10这10个自然数中,每次取两个数,使得所取两数之和大于10,共有多少种取法?
(2)在1~100这100个自然数中,每次取两个数,使得所取两数之和大于100,共有多少种取法?
(3)你还能提出什么问题?
(4)各边长度都是整数、最大边长为11的三角形有多少个?本题与上述哪个问题有联系?它们的区别是什么?
14.甲、乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做游戏.游戏规则是:将4张牌的正面全部朝下,洗匀,先从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下,洗匀,再从中随机抽取一张,抽得的数字作为个位上的数字,这样就得到一个两位数.
(1)用列表或画树状图的方法表示出所有可能出现的结果;
(2)若这个两位数小于50,则甲获胜,否则乙获胜,你认为这个游戏公平吗?为什么?
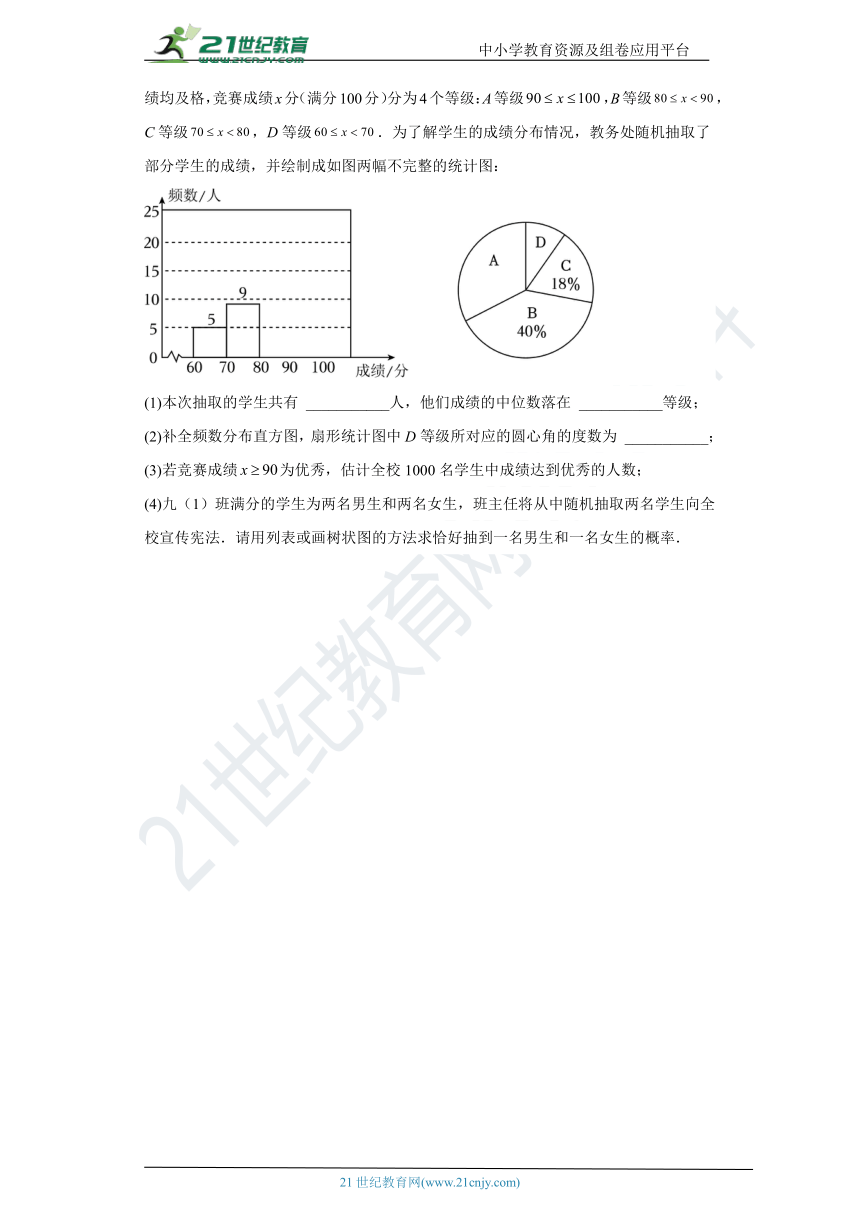
15.宪法是国家的根本法,是治国安邦的总章程.学法辨是非、知法明荣辱、守法正社风、用法止纷争,弘扬并践行宪法精神是当代青少年的义务与担当.某校举行以“学宪法,讲宪法”为主题的宣传教育活动,并举办了宪法知识竞赛.据统计:所有学生的成绩均及格,竞赛成绩x分(满分100分)分为4个等级:A等级,B等级,C等级,D等级.为了解学生的成绩分布情况,教务处随机抽取了部分学生的成绩,并绘制成如图两幅不完整的统计图:
(1)本次抽取的学生共有 ___________人,他们成绩的中位数落在 ___________等级;
(2)补全频数分布直方图,扇形统计图中D等级所对应的圆心角的度数为 ___________;
(3)若竞赛成绩为优秀,估计全校1000名学生中成绩达到优秀的人数;
(4)九(1)班满分的学生为两名男生和两名女生,班主任将从中随机抽取两名学生向全校宣传宪法.请用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】分析左图可知,1个“ ”的质量等于2个“○”的质量.两个物体等可能的向左或向右落时,共有4种情况,分别计算出左边托盘和右边托盘的质量,即可得出和的关系.
【详解】解:由左图可知2个“○”与1个“ ”的质量等于2个“ ”的质量,
1个“ ”的质量等于2个“○”的质量.
右图中,两个物体等可能的向左或向右落在下面的托盘中,
共有4种情况:
(1)“○”和“ ”都落到左边的托盘时:
左边有3个“○”2个“ ”,相当于7个“○”,右边有2个“ ”,相当于4个“○”,此时;
(2)“○”和“ ”都落到右边的托盘时:
左边有2个“○”1个“ ”,相当于4个“○”,右边有3个“ ” 1个“○”,相当于7个“○”,此时;
(3)“○”落到左边的托盘,“ ” 落到右边的托盘时:
左边有3个“○”1个“ ”,相当于5个“○”,右边有3个“ ”,相当于6个“○”,此时;
(4)“○”落到右边的托盘,“ ” 落到左边的托盘时:
左边有2个“○”2个“ ”,相当于6个“○”,右边有2个“ ” 1个“○”,相当于5个“○”,此时;
观察四个选项可知,只有选项C符合题意,
故选C.
【点睛】本题考查等可能事件、等式的性质,解题的关键是读懂题意,计算所有等可能情况下和的比值.
2.A
【详解】A选项中,一个瓶盖可用盖面朝上表示硬币的正面,盖面朝下表示硬币的反面,两者出现的概率一样,可作实验替代物,所以本选项正确;
B选项中,图钉尖朝上的概率大于面朝上的概率,不可做实验替代物,所以本选项错误;
C选项中,用计算器产生1和2两个随机整数,1代表正面,2代表反面,两数产生的概率不同,不能代替抛掷硬币的实验,所以本选项错误;
D选项中,转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面,由于还有一个“黄色区域”,本实验中有三种等可能结果,与抛掷硬币实验情况不一样,所以本选项错误;
故选A.
3.D
【分析】直接利用概率的意义以及必然事件、全面调查的意义分别分析得出答案.
【详解】解:A.为了了解我国中学生的课外阅读情况,应采取抽样调查方式,原说法错误,故此选项不合题意;
B.某彩票的中奖机会是,买100张也不一定会中奖,原说法错误,故此选项不合题意;
C.若a是实数,则是随机事件,原说法错误,故此选项不合题意;
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定,故此选项符合题意,
故选:D.
【点睛】此题主要考查了概率的意义以及方差,正确掌握概率的意义是解题关键.
4.D
【分析】根据概率的意义、全面调查和抽样调查的概念以及实现的可能性、样本容量的概念逐项判断即可.
【详解】解:A. 小明投篮投中的概率是0.6,说明他投10次篮球不一定能中6次,A错误;
B. 为了解全国中学生的节水意识,应采用抽样调查的方式,B错误;
C. 为了解某校300名九年级学生的睡眠时间,从中抽取50名九年级学生进行调查,在这个事件中,样本容量是50,C错误;
D. 一个不透明口袋中装有3个红球2个白球,除颜色外都相同,从中任意摸出一个球,摸到红球的可能性比白球大,D正确.
故答案为D.
【点睛】本题主要考查了根据概率的意义、全面调查和抽样调查的概念以及实现的可能性、样本容量等知识点,灵活理解相关概念成为解答本题的关键.
5.B
【分析】分析各个选项中的概率之和即可选出不成功的选项.
【详解】A.;
B.,不成立;
C.;
D.;
故选:B.
【点睛】本题考查简单事件的概率.一次试验中有n种等可能的结果,每种结果出现的概率之和为1.
6.D
【分析】列出表格,共有12种等可能的结果,其中女同学杨玲和男同学张军恰好来自同一班级,被同时抽中的结果有2种,再由概率公式求解即可.
【详解】解:根据题意,列出表格如下:
男1 男2 男张军 女1 女杨玲
男1 男1,女1 男1,女杨玲
男2 男2,女1 男2,女杨玲
男张军 男张军,女1 男张军,女杨玲
女1 女1,男1 女1,男2 女1,男张军
女杨玲 女杨玲,男1 女杨玲,男2 女杨玲,男张军
共有12种等可能的结果,其中女同学杨玲和男同学张军恰好来自同一班级,被同时抽中的结果有2种,
女同学杨玲和男同学张军恰好来自同一班级,他俩同时被抽中的概率为:,
故选:D.
【点睛】本题主要考查了列表法求概率,根据题意正确的列出所有可能的结果是解题的关键.
7.A
【分析】画树状图得出所有等可能的结果数,再从中找到符合条件的结果数,然后再用概率公式求解即可.
【详解】解:树状图如图所示,
一共有12种等可能性,其中王明选中的卡片中有偶数的可能性有10种可能性,
故王明选中的卡片中有偶数的概率为:,
故选:A.
【点睛】本题主要考查的是用列表法或树状图法求概率,列表法可以重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,用到的知识点为:概率等于所求情况数与总情况数之比.
8.C
【分析】按照题意分别找出点C所在的位置的个数,再找出其中满足的面积为1的C点个数,再根据概率公式求出概率即可.
【详解】解:如图所示,
点C所放在格点上的位置共有16种可能,而能使△ABC的面积为1的点共有如图4种可能,
故恰好使△ABC的面积为1的概率为:.
故本题正确答案为C.
【点睛】熟练掌握三角形的基本概念和求随机事件的概率是解本题的关键.
9.白
【分析】分别计算出摸到红、白、黑球的可能性,比较大小后即可得到答案.
【详解】∵袋子中装有个红球、个白球和个黑球,
∴摸出红球的可能性是:2÷(2+5+3)=,
摸出白球的可能性是:5÷(2+5+3)=,
摸出黑球的可能性是:3÷(2+5+3)=,
∵>>,
∴白球出现的可能性大.
故答案为:白
【点睛】本题主要考查了求简单事件发生的可能性,用到的知识点为:可能性等于所求情况数与总情况数之比.
10.①④
【分析】根据确定事件的定义(必然事件和不可能事件统称为确定事件),一一判断即可得到答案;
【详解】解:①如果、都是实数,那么,是必然事件;
②打开电视,正在播放新闻,是随机事件;
③抛掷一枚硬币,正面向上,是随机事件;
④张相同的小标签分别标有数字,从中任意抽取张,抽到号签,是不可能事件;
故确定事件有①④,
故答案为:①④;
【点睛】本题主要考查了确定事件的定义,即必然事件和不可能事件统称为相对条件S的确定事件,掌握确定事件的定义是解题的关键;
11.30
【分析】先求出飞机失事时保险公司应赔偿的金额,再根据飞机失事的概率求出赔偿的钱数即可解答.
【详解】解:每次约有200名乘客,如飞机一旦失事,每位乘客赔偿60万人民币,共计12000万元,
一次飞行中飞机失事的概率为,
故赔偿的钱数为元,
故至少应该收取保险费每人元,
故答案为:30.
【点睛】本题考查的是概率在现实生活中的运用,部分数目=总体数目乘以相应概率.
12.
【分析】利用列表表或画树状图求概率即可.
【详解】解:列表如下:
1 2 3
1 1,1 1,2 1,3
2 2,1 2,2 2,3
3 3,1 3,2 3,3
由表知,所有等可能的结果数有9种,其中和为4的结果数有3种,则摸出的两球的数字之和是4的概率是;
故答案为:.
【点睛】本题考查了用列表法或画树状图求较复杂事件的概率,正确列表或画出树状图是关键.
13.(1);(2);(3)见解析;(4)36,见解析
【分析】(1)仔细分析题意,可先取出一个数,根据取出的这个数来确定另一个数的可能取值,取第一个数为10,则第二个数可以为1,2,……,9,同理第一个数取9,可以发现若第一个数为10,则可能的取法有9种,若第一个数取9,则可能的取法有7种,若第一个数取8,可能的取法有5种,……,将所有类别的取法相加,即可求得结果;
(2)利用类似于(1)的方法进行分析即可解答;
(3)提一个类似于(1)(2)的问题即可;
(4)结合(1)、(2)的方法,注意要考虑两边相等的情况
【详解】(1)根据题意每次取的两个数之和大于10,可能取法为:
10+1、10+2、10+3、…10+9,共9种
9+2、 9+3、 9+4、 …9+8,共7种
8+3、8+4、8+5、8+6、8+7,共5种
7+4、7+5、7+6,共3种
6+5,共1种
所以可能的取法共有9+7+5+3+1=(种)
(2)同理可得可能的取法的种数为=2500(种)
(3)(答案不唯一)在1到21这21个自然数中,每次取两个不同的数,使得所取的两个数之和大于21,有多少种不同的取法?
(4)根据题意得:①每次取两个不同的数,使得所取的两个数之和大于11,有10+8+6+4+2=30种不同的取法;
②若另两个数相同,则6+6,7+7,…,11+11,共6种不同的取法;所以各边长都是整数,最大边长为11的三角形有:30+6=36(个).
它与上述两个问题都类似,区别这个问题要考虑两个数相同时的情况.
【点睛】此题考查分类加法计数原理的运用.分类加法计数原理:完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有m1+m2+……+mn种不同的方法.注意分类后,寻找规律,避免大量运算,其次注意分类讨论要不重不漏.
14.(1)见解析
(2)这个游戏公平,理由见解析
【分析】(1)列表格表示出所有可能出现的结果即可;
(2)游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】(1)解:所有可能出现的结果列表如下:
两位数 3 4 5 6
3 33 34 35 36
4 43 44 45 46
5 53 54 55 56
6 63 64 65 66
由表格可知,共有16种等可能出现的结果;
(2)由(1)可知这个两位数小于50的有8种,
,
这个游戏公平.
【点睛】本题考查了概率,解题的关键是掌握判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
15.(1)50,B
(2)见解析,36°
(3)320
(4)
【分析】(1)由C等级人数及其所占百分比可得总人数,再求出B等级人数,依据中位数的定义可得答案;
(2)根据(1)中所求结果即可补全图形,用360°乘以D等级人数所占比例即可得出答案;
(3)用总人数乘以样本中A等级人数所占比例即可;
(4)画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)本次抽取的学生人数为(人),
则B等级人数为(人),A等级人数为(人),
成绩的中位数是第25、26个数据的平均数,而这两个数据落在B等级,所以他们成绩的中位数落在B等级,
故答案为:50、B;
(2)补全直方图如下:
扇形统计图中D等级所对应的圆心角的度数为,
故答案为:;
(3)(人),
答:估计全校1000名学生中成绩达到优秀的人数为320人;
(4)画树状图为:
共有12种等可能的结果,其中一名男生和一名女生的结果数为8,所以恰好抽到一名男生和一名女生的概率为.
【点睛】本题考查了统计图,样本估计总体,中位数,列表法与树状图法求概率:利用列表法或树状图法展示所有可能的结果是解题的关键,总体结果数为n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第4章等可能条件下的概率 单元精选精练卷 2023-2024学年苏科版(2012)九年级数学上册
一、单选题
1.如左图的天平架是平衡的,其中同一种物体的质量都相等,如右图,现将不同质量的一“○”和一个“”从通道的顶端同时放下,两个物体等可能的向左或向右落在下面的托盘中,此时两个托盘上物体的质量分别为和,则下列关系可能出现的是( )
A. B. C. D.
2.如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )
A.掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B.掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C.用计算器产生1和2两个随机整数,1代表正面,2代表反面
D.转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面
3.下列说法中正确的是( )
A.为了了解我国中学生的课外阅读情况,应采取全面调查方式
B.某彩票的中奖机会是,买100张一定会中奖
C.若a是实数,则是必然事件
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定
4.下列说法正确的是( )
A.小明投篮投中的概率是0.6,说明他投10次篮球一定能中6次
B.为了解全国中学生的节水意识,应采用普查的方式
C.为了解某校300名九年级学生的睡眠时间,从中抽取50名九年级学生进行调查,在这个事件中,样本容量是300
D.一个不透明口袋中装有3个红球2个白球,除颜色外都相同,从中任意摸出一个球,摸到红球的可能性比白球大
5.李明用6个球设计了一个摸球游戏,共有四种方案,肯定不能成功的是( )
A.摸到黄球、红球的概率均为
B.摸到黄球的概率是,摸到红球、白球的概率均为
C.摸到黄球、红球、白球的概率分别为、、
D.摸到黄球、红球、白球的概率都是
6.合肥市某校九年级(1)、(2)班共有2名女生和3名男生分别被评为“智慧之星”,要从这5位学生中随机抽取一男一女两位学生做获奖感言,女同学杨玲和男同学张军恰好来自同一班级,则他俩同时被抽中的概率为( )
A. B. C. D.
7.四张背面完全相同的卡片上分别写有1、2、3、4四个数字,把卡片背面朝上洗匀后,王明从这四张卡片中随机选两张,则王明选中的卡片中有偶数的概率是( )
A. B. C. D.
8.在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为( ).
A. B. C. D.
二、填空题
9.在一个不透明的袋子中装有个红球、个白球和个黑球,这些球除颜色外都相同.从中任意摸出个球,摸到 色的球的可能性最大.(填“红”、“白”或“黑”)
10.下列事件:
①如果、都是实数,那么;
②打开电视,正在播放新闻;
③抛掷一枚硬币,正面向上;
④张相同的小标签分别标有数字,从中任意抽取张,抽到号签.
属于确定事件的是 (填序号)
11.某航班每次约有200名乘客,一次飞行中飞机失事的概率,某保险公司为乘客提供保险,承诺飞机一旦失事,向每位乘客赔偿60万人民币.平均来说,保险公司应该至少向每位乘客收取 元保险费才不亏本.
12.在一个不透明的口袋中,装有3个球,它们分别写有数字1,2,3,这些球除上面数字外,其余都相同.先将这些球摇匀后,随机摸出一球,记下数字后,放回:再摇匀,再摸出一球.则摸出的两球的数字之和是4的概率是 .
三、解答题
13.求解下列问题:
(1)在1~10这10个自然数中,每次取两个数,使得所取两数之和大于10,共有多少种取法?
(2)在1~100这100个自然数中,每次取两个数,使得所取两数之和大于100,共有多少种取法?
(3)你还能提出什么问题?
(4)各边长度都是整数、最大边长为11的三角形有多少个?本题与上述哪个问题有联系?它们的区别是什么?
14.甲、乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做游戏.游戏规则是:将4张牌的正面全部朝下,洗匀,先从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下,洗匀,再从中随机抽取一张,抽得的数字作为个位上的数字,这样就得到一个两位数.
(1)用列表或画树状图的方法表示出所有可能出现的结果;
(2)若这个两位数小于50,则甲获胜,否则乙获胜,你认为这个游戏公平吗?为什么?
15.宪法是国家的根本法,是治国安邦的总章程.学法辨是非、知法明荣辱、守法正社风、用法止纷争,弘扬并践行宪法精神是当代青少年的义务与担当.某校举行以“学宪法,讲宪法”为主题的宣传教育活动,并举办了宪法知识竞赛.据统计:所有学生的成绩均及格,竞赛成绩x分(满分100分)分为4个等级:A等级,B等级,C等级,D等级.为了解学生的成绩分布情况,教务处随机抽取了部分学生的成绩,并绘制成如图两幅不完整的统计图:
(1)本次抽取的学生共有 ___________人,他们成绩的中位数落在 ___________等级;
(2)补全频数分布直方图,扇形统计图中D等级所对应的圆心角的度数为 ___________;
(3)若竞赛成绩为优秀,估计全校1000名学生中成绩达到优秀的人数;
(4)九(1)班满分的学生为两名男生和两名女生,班主任将从中随机抽取两名学生向全校宣传宪法.请用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】分析左图可知,1个“ ”的质量等于2个“○”的质量.两个物体等可能的向左或向右落时,共有4种情况,分别计算出左边托盘和右边托盘的质量,即可得出和的关系.
【详解】解:由左图可知2个“○”与1个“ ”的质量等于2个“ ”的质量,
1个“ ”的质量等于2个“○”的质量.
右图中,两个物体等可能的向左或向右落在下面的托盘中,
共有4种情况:
(1)“○”和“ ”都落到左边的托盘时:
左边有3个“○”2个“ ”,相当于7个“○”,右边有2个“ ”,相当于4个“○”,此时;
(2)“○”和“ ”都落到右边的托盘时:
左边有2个“○”1个“ ”,相当于4个“○”,右边有3个“ ” 1个“○”,相当于7个“○”,此时;
(3)“○”落到左边的托盘,“ ” 落到右边的托盘时:
左边有3个“○”1个“ ”,相当于5个“○”,右边有3个“ ”,相当于6个“○”,此时;
(4)“○”落到右边的托盘,“ ” 落到左边的托盘时:
左边有2个“○”2个“ ”,相当于6个“○”,右边有2个“ ” 1个“○”,相当于5个“○”,此时;
观察四个选项可知,只有选项C符合题意,
故选C.
【点睛】本题考查等可能事件、等式的性质,解题的关键是读懂题意,计算所有等可能情况下和的比值.
2.A
【详解】A选项中,一个瓶盖可用盖面朝上表示硬币的正面,盖面朝下表示硬币的反面,两者出现的概率一样,可作实验替代物,所以本选项正确;
B选项中,图钉尖朝上的概率大于面朝上的概率,不可做实验替代物,所以本选项错误;
C选项中,用计算器产生1和2两个随机整数,1代表正面,2代表反面,两数产生的概率不同,不能代替抛掷硬币的实验,所以本选项错误;
D选项中,转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面,由于还有一个“黄色区域”,本实验中有三种等可能结果,与抛掷硬币实验情况不一样,所以本选项错误;
故选A.
3.D
【分析】直接利用概率的意义以及必然事件、全面调查的意义分别分析得出答案.
【详解】解:A.为了了解我国中学生的课外阅读情况,应采取抽样调查方式,原说法错误,故此选项不合题意;
B.某彩票的中奖机会是,买100张也不一定会中奖,原说法错误,故此选项不合题意;
C.若a是实数,则是随机事件,原说法错误,故此选项不合题意;
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定,故此选项符合题意,
故选:D.
【点睛】此题主要考查了概率的意义以及方差,正确掌握概率的意义是解题关键.
4.D
【分析】根据概率的意义、全面调查和抽样调查的概念以及实现的可能性、样本容量的概念逐项判断即可.
【详解】解:A. 小明投篮投中的概率是0.6,说明他投10次篮球不一定能中6次,A错误;
B. 为了解全国中学生的节水意识,应采用抽样调查的方式,B错误;
C. 为了解某校300名九年级学生的睡眠时间,从中抽取50名九年级学生进行调查,在这个事件中,样本容量是50,C错误;
D. 一个不透明口袋中装有3个红球2个白球,除颜色外都相同,从中任意摸出一个球,摸到红球的可能性比白球大,D正确.
故答案为D.
【点睛】本题主要考查了根据概率的意义、全面调查和抽样调查的概念以及实现的可能性、样本容量等知识点,灵活理解相关概念成为解答本题的关键.
5.B
【分析】分析各个选项中的概率之和即可选出不成功的选项.
【详解】A.;
B.,不成立;
C.;
D.;
故选:B.
【点睛】本题考查简单事件的概率.一次试验中有n种等可能的结果,每种结果出现的概率之和为1.
6.D
【分析】列出表格,共有12种等可能的结果,其中女同学杨玲和男同学张军恰好来自同一班级,被同时抽中的结果有2种,再由概率公式求解即可.
【详解】解:根据题意,列出表格如下:
男1 男2 男张军 女1 女杨玲
男1 男1,女1 男1,女杨玲
男2 男2,女1 男2,女杨玲
男张军 男张军,女1 男张军,女杨玲
女1 女1,男1 女1,男2 女1,男张军
女杨玲 女杨玲,男1 女杨玲,男2 女杨玲,男张军
共有12种等可能的结果,其中女同学杨玲和男同学张军恰好来自同一班级,被同时抽中的结果有2种,
女同学杨玲和男同学张军恰好来自同一班级,他俩同时被抽中的概率为:,
故选:D.
【点睛】本题主要考查了列表法求概率,根据题意正确的列出所有可能的结果是解题的关键.
7.A
【分析】画树状图得出所有等可能的结果数,再从中找到符合条件的结果数,然后再用概率公式求解即可.
【详解】解:树状图如图所示,
一共有12种等可能性,其中王明选中的卡片中有偶数的可能性有10种可能性,
故王明选中的卡片中有偶数的概率为:,
故选:A.
【点睛】本题主要考查的是用列表法或树状图法求概率,列表法可以重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,用到的知识点为:概率等于所求情况数与总情况数之比.
8.C
【分析】按照题意分别找出点C所在的位置的个数,再找出其中满足的面积为1的C点个数,再根据概率公式求出概率即可.
【详解】解:如图所示,
点C所放在格点上的位置共有16种可能,而能使△ABC的面积为1的点共有如图4种可能,
故恰好使△ABC的面积为1的概率为:.
故本题正确答案为C.
【点睛】熟练掌握三角形的基本概念和求随机事件的概率是解本题的关键.
9.白
【分析】分别计算出摸到红、白、黑球的可能性,比较大小后即可得到答案.
【详解】∵袋子中装有个红球、个白球和个黑球,
∴摸出红球的可能性是:2÷(2+5+3)=,
摸出白球的可能性是:5÷(2+5+3)=,
摸出黑球的可能性是:3÷(2+5+3)=,
∵>>,
∴白球出现的可能性大.
故答案为:白
【点睛】本题主要考查了求简单事件发生的可能性,用到的知识点为:可能性等于所求情况数与总情况数之比.
10.①④
【分析】根据确定事件的定义(必然事件和不可能事件统称为确定事件),一一判断即可得到答案;
【详解】解:①如果、都是实数,那么,是必然事件;
②打开电视,正在播放新闻,是随机事件;
③抛掷一枚硬币,正面向上,是随机事件;
④张相同的小标签分别标有数字,从中任意抽取张,抽到号签,是不可能事件;
故确定事件有①④,
故答案为:①④;
【点睛】本题主要考查了确定事件的定义,即必然事件和不可能事件统称为相对条件S的确定事件,掌握确定事件的定义是解题的关键;
11.30
【分析】先求出飞机失事时保险公司应赔偿的金额,再根据飞机失事的概率求出赔偿的钱数即可解答.
【详解】解:每次约有200名乘客,如飞机一旦失事,每位乘客赔偿60万人民币,共计12000万元,
一次飞行中飞机失事的概率为,
故赔偿的钱数为元,
故至少应该收取保险费每人元,
故答案为:30.
【点睛】本题考查的是概率在现实生活中的运用,部分数目=总体数目乘以相应概率.
12.
【分析】利用列表表或画树状图求概率即可.
【详解】解:列表如下:
1 2 3
1 1,1 1,2 1,3
2 2,1 2,2 2,3
3 3,1 3,2 3,3
由表知,所有等可能的结果数有9种,其中和为4的结果数有3种,则摸出的两球的数字之和是4的概率是;
故答案为:.
【点睛】本题考查了用列表法或画树状图求较复杂事件的概率,正确列表或画出树状图是关键.
13.(1);(2);(3)见解析;(4)36,见解析
【分析】(1)仔细分析题意,可先取出一个数,根据取出的这个数来确定另一个数的可能取值,取第一个数为10,则第二个数可以为1,2,……,9,同理第一个数取9,可以发现若第一个数为10,则可能的取法有9种,若第一个数取9,则可能的取法有7种,若第一个数取8,可能的取法有5种,……,将所有类别的取法相加,即可求得结果;
(2)利用类似于(1)的方法进行分析即可解答;
(3)提一个类似于(1)(2)的问题即可;
(4)结合(1)、(2)的方法,注意要考虑两边相等的情况
【详解】(1)根据题意每次取的两个数之和大于10,可能取法为:
10+1、10+2、10+3、…10+9,共9种
9+2、 9+3、 9+4、 …9+8,共7种
8+3、8+4、8+5、8+6、8+7,共5种
7+4、7+5、7+6,共3种
6+5,共1种
所以可能的取法共有9+7+5+3+1=(种)
(2)同理可得可能的取法的种数为=2500(种)
(3)(答案不唯一)在1到21这21个自然数中,每次取两个不同的数,使得所取的两个数之和大于21,有多少种不同的取法?
(4)根据题意得:①每次取两个不同的数,使得所取的两个数之和大于11,有10+8+6+4+2=30种不同的取法;
②若另两个数相同,则6+6,7+7,…,11+11,共6种不同的取法;所以各边长都是整数,最大边长为11的三角形有:30+6=36(个).
它与上述两个问题都类似,区别这个问题要考虑两个数相同时的情况.
【点睛】此题考查分类加法计数原理的运用.分类加法计数原理:完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有m1+m2+……+mn种不同的方法.注意分类后,寻找规律,避免大量运算,其次注意分类讨论要不重不漏.
14.(1)见解析
(2)这个游戏公平,理由见解析
【分析】(1)列表格表示出所有可能出现的结果即可;
(2)游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】(1)解:所有可能出现的结果列表如下:
两位数 3 4 5 6
3 33 34 35 36
4 43 44 45 46
5 53 54 55 56
6 63 64 65 66
由表格可知,共有16种等可能出现的结果;
(2)由(1)可知这个两位数小于50的有8种,
,
这个游戏公平.
【点睛】本题考查了概率,解题的关键是掌握判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
15.(1)50,B
(2)见解析,36°
(3)320
(4)
【分析】(1)由C等级人数及其所占百分比可得总人数,再求出B等级人数,依据中位数的定义可得答案;
(2)根据(1)中所求结果即可补全图形,用360°乘以D等级人数所占比例即可得出答案;
(3)用总人数乘以样本中A等级人数所占比例即可;
(4)画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)本次抽取的学生人数为(人),
则B等级人数为(人),A等级人数为(人),
成绩的中位数是第25、26个数据的平均数,而这两个数据落在B等级,所以他们成绩的中位数落在B等级,
故答案为:50、B;
(2)补全直方图如下:
扇形统计图中D等级所对应的圆心角的度数为,
故答案为:;
(3)(人),
答:估计全校1000名学生中成绩达到优秀的人数为320人;
(4)画树状图为:
共有12种等可能的结果,其中一名男生和一名女生的结果数为8,所以恰好抽到一名男生和一名女生的概率为.
【点睛】本题考查了统计图,样本估计总体,中位数,列表法与树状图法求概率:利用列表法或树状图法展示所有可能的结果是解题的关键,总体结果数为n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
