12.2 三角形全等的判定 同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.2 三角形全等的判定 同步练习 2023-2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 19:02:13 | ||
图片预览


文档简介
12.2 三角形全等的判定 同步练习 2022-2023学年人教版数学八年级上册
一、单选题
1.下面的两个三角形一定全等的是( )
A.腰相等的两个等腰三角形
B.一个角对应相等的两个等腰三角形
C.斜边对应相等的两个直角三角形
D.底边相等的两个等腰直角三角形
2.如图,下列条件中,不能证明 ≌ 的条件是( )
A.AB DC,AC DB B.AB DC,
C.AB DC, D. ,
3.如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
A.120° B.125° C.130° D.155°
4.如图,和中,,,若,则等于( )
A.10° B.20° C.30° D.40°
5.如图是用尺规作一个角的角平分线的示意图,其根据是构造两个三角形全等.由作法知,能判定△MOC≌△NOC的依据是( )
A.SAS B.SSS C.ASA D.AAS
6.如图,点分别在线段上,与相交于点.若,且,,则的度数为( )
A. B. C. D.
7.如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
8.如图,点A,E,C在同一直线上,,,,则BC的长为( )
A.3 B.5 C.8 D.11
二、填空题
9.如图,已知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AED
10.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图7,则∠EAB是多少度?请你说出∠EAB= 度
11.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 .
12.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CF⊥AD,BE⊥AD.若CF=8,BE=6,AD=10,则EF的长为 .
13.如图,Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于E,BD⊥CF,AF⊥CF,则下列结论:①∠ACF=∠CBD②BD=FC③FC=FD+AF④AE=DC中,正确的结论是 (填正确结论的编号)
三、解答题
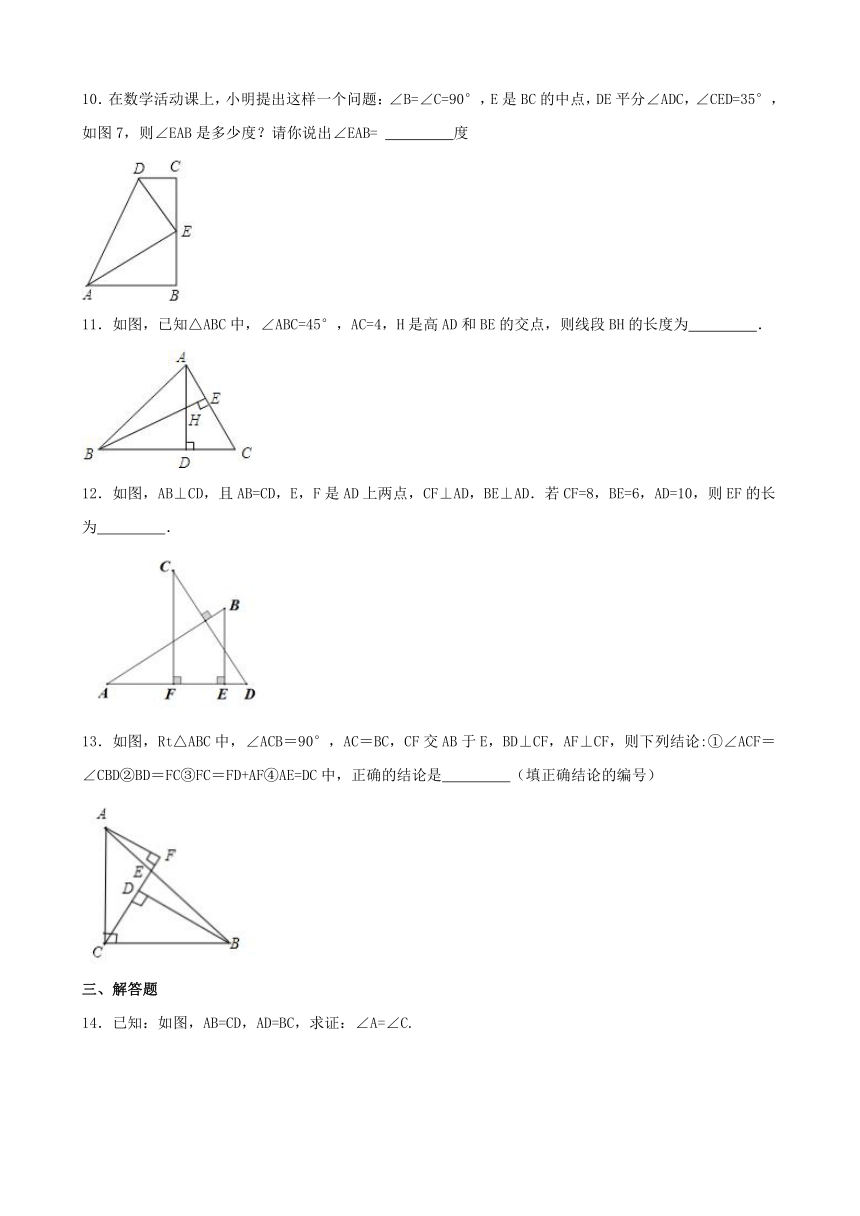
14.已知:如图,AB=CD,AD=BC,求证:∠A=∠C.
15.已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
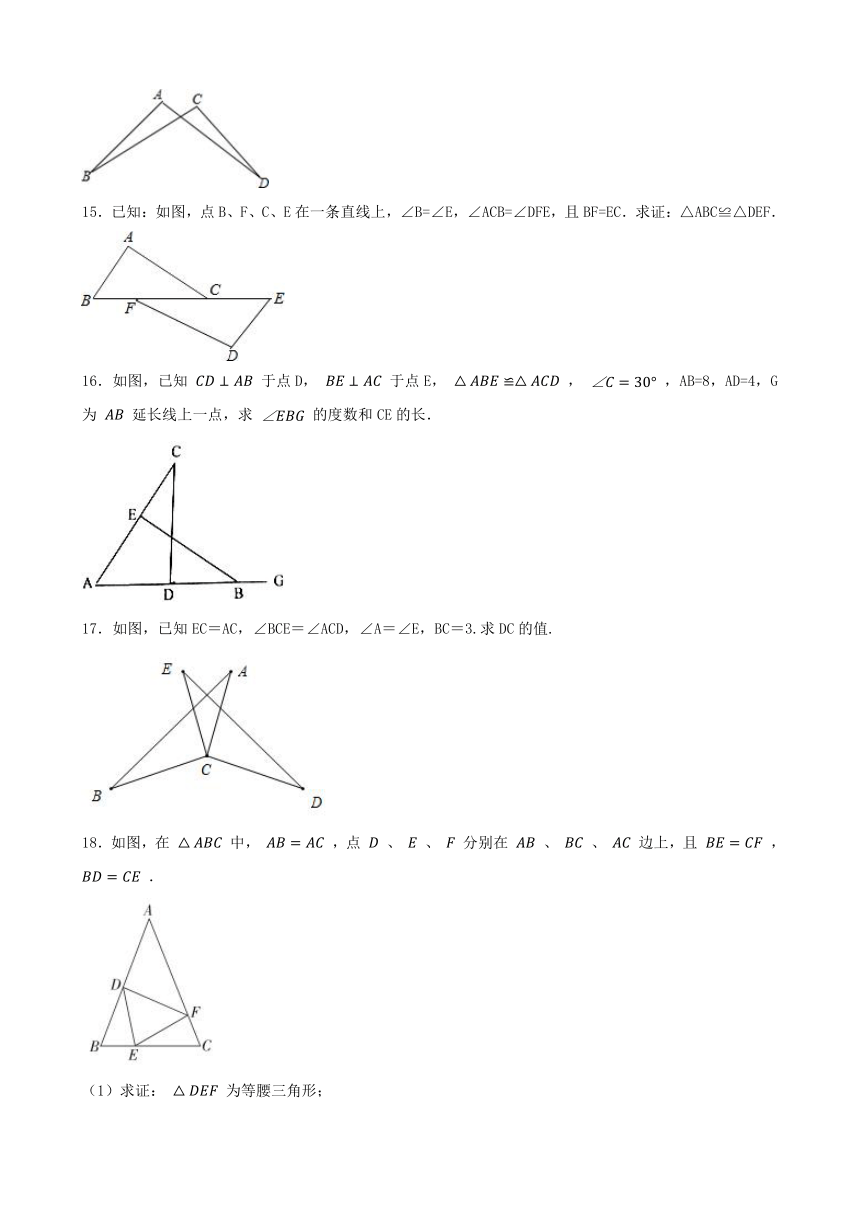
16.如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长.
17.如图,已知EC=AC,∠BCE=∠ACD,∠A=∠E,BC=3.求DC的值.
18.如图,在 中, ,点 、 、 分别在 、 、 边上,且 , .
(1)求证: 为等腰三角形;
(2)当 时,求 的度数.
19.在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,
求AD的取值范围.小明给出了一种方法,步骤如下:
①过点C作一条与AB平行的线;
②延长AD交这条平行线于点E;
③通过证明得到AD=DE,AB=CE;
④利用△ACE三边的数量关系得到AD的取值范围.
根据这个方法,请你完成下面两个问题:
(1)求证:AD=DE,AB=CE;
(2)求AD的取值范围.
参考答案
1.D
2.C
3.C
4.B
5.B
6.C
7.C
8.B
9.AB=AE
10.35
11.4
12.4
13.①②③
14.证明:连接BD,
在 ABD和 CDB中,
∴ ABD≌ CDB(SSS),
∴∠A=∠C
15.证明:∵BF=EC
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA)
16.解:∵△ABE≌△ACD,∠C=30°,AB=8,AD=4,
∴∠ABE=∠C=30°,
∴∠EBG=180°-∠ABE=180°-30°=150°,
∴AE=AD=4,AC=AB=8,
∴CE=AC-AE=8-4=4.
17.解:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD +∠ACE,即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(ASA),
∴BC=DC=3.
18.(1)证明:∵ ,
∴ ,
在 和 中,
,
∴ ( ),
∴ ,
∴ 为等腰三角形
(2)解:∵ ,
∴ ,
∵ 是 的外角,
∴ ,
∴ ,
∴ ,
在 中 ,
∴ ,
∴
19.(1)证明:∵AB∥CD,
∴∠B=∠DCE,
在△ADB和△EDC中,
,
∴△ADB≌△EDC(ASA),
∴AD=DE,AB=CE.
(2)解:∵AC=9,EC=AB=5,
∴9﹣5<AE<5+9,
∴4<AE<14,
∵AD=DE,
∴AE=2AD,
∴4<2AD<14,
∴2<AD<7
一、单选题
1.下面的两个三角形一定全等的是( )
A.腰相等的两个等腰三角形
B.一个角对应相等的两个等腰三角形
C.斜边对应相等的两个直角三角形
D.底边相等的两个等腰直角三角形
2.如图,下列条件中,不能证明 ≌ 的条件是( )
A.AB DC,AC DB B.AB DC,
C.AB DC, D. ,
3.如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
A.120° B.125° C.130° D.155°
4.如图,和中,,,若,则等于( )
A.10° B.20° C.30° D.40°
5.如图是用尺规作一个角的角平分线的示意图,其根据是构造两个三角形全等.由作法知,能判定△MOC≌△NOC的依据是( )
A.SAS B.SSS C.ASA D.AAS
6.如图,点分别在线段上,与相交于点.若,且,,则的度数为( )
A. B. C. D.
7.如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
8.如图,点A,E,C在同一直线上,,,,则BC的长为( )
A.3 B.5 C.8 D.11
二、填空题
9.如图,已知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AED
10.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图7,则∠EAB是多少度?请你说出∠EAB= 度
11.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 .
12.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CF⊥AD,BE⊥AD.若CF=8,BE=6,AD=10,则EF的长为 .
13.如图,Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于E,BD⊥CF,AF⊥CF,则下列结论:①∠ACF=∠CBD②BD=FC③FC=FD+AF④AE=DC中,正确的结论是 (填正确结论的编号)
三、解答题
14.已知:如图,AB=CD,AD=BC,求证:∠A=∠C.
15.已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
16.如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长.
17.如图,已知EC=AC,∠BCE=∠ACD,∠A=∠E,BC=3.求DC的值.
18.如图,在 中, ,点 、 、 分别在 、 、 边上,且 , .
(1)求证: 为等腰三角形;
(2)当 时,求 的度数.
19.在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,
求AD的取值范围.小明给出了一种方法,步骤如下:
①过点C作一条与AB平行的线;
②延长AD交这条平行线于点E;
③通过证明得到AD=DE,AB=CE;
④利用△ACE三边的数量关系得到AD的取值范围.
根据这个方法,请你完成下面两个问题:
(1)求证:AD=DE,AB=CE;
(2)求AD的取值范围.
参考答案
1.D
2.C
3.C
4.B
5.B
6.C
7.C
8.B
9.AB=AE
10.35
11.4
12.4
13.①②③
14.证明:连接BD,
在 ABD和 CDB中,
∴ ABD≌ CDB(SSS),
∴∠A=∠C
15.证明:∵BF=EC
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA)
16.解:∵△ABE≌△ACD,∠C=30°,AB=8,AD=4,
∴∠ABE=∠C=30°,
∴∠EBG=180°-∠ABE=180°-30°=150°,
∴AE=AD=4,AC=AB=8,
∴CE=AC-AE=8-4=4.
17.解:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD +∠ACE,即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(ASA),
∴BC=DC=3.
18.(1)证明:∵ ,
∴ ,
在 和 中,
,
∴ ( ),
∴ ,
∴ 为等腰三角形
(2)解:∵ ,
∴ ,
∵ 是 的外角,
∴ ,
∴ ,
∴ ,
在 中 ,
∴ ,
∴
19.(1)证明:∵AB∥CD,
∴∠B=∠DCE,
在△ADB和△EDC中,
,
∴△ADB≌△EDC(ASA),
∴AD=DE,AB=CE.
(2)解:∵AC=9,EC=AB=5,
∴9﹣5<AE<5+9,
∴4<AE<14,
∵AD=DE,
∴AE=2AD,
∴4<2AD<14,
∴2<AD<7
