11.1 与三角形有关的线段 同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.1 与三角形有关的线段 同步练习 2023-2024学年人教版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览

文档简介
11.1 与三角形有关的线段 同步练习 2022-2023学年人教版数学八年级上册
一、单选题
1.下列长度的三条线段中,能围成三角形的是( )
A.5cm,6cm,12cm B.3cm,4cm,5cm
C.4cm,6cm,10cm D.3cm,4cm,8cm
2.若三条线段中a=3,b=5,为奇数,那么由a、b、c为边组成的三角形共有( )
A.个 B.个 C.无数多个 D.无法确定
3.如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( )
A.12米 B.10米 C.20米 D.8米
4.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,AD是△ABC的角平分线,则( )
A.∠1=∠BAC B.∠1=∠ABC C.∠1=∠BAC D.∠1=∠ABC
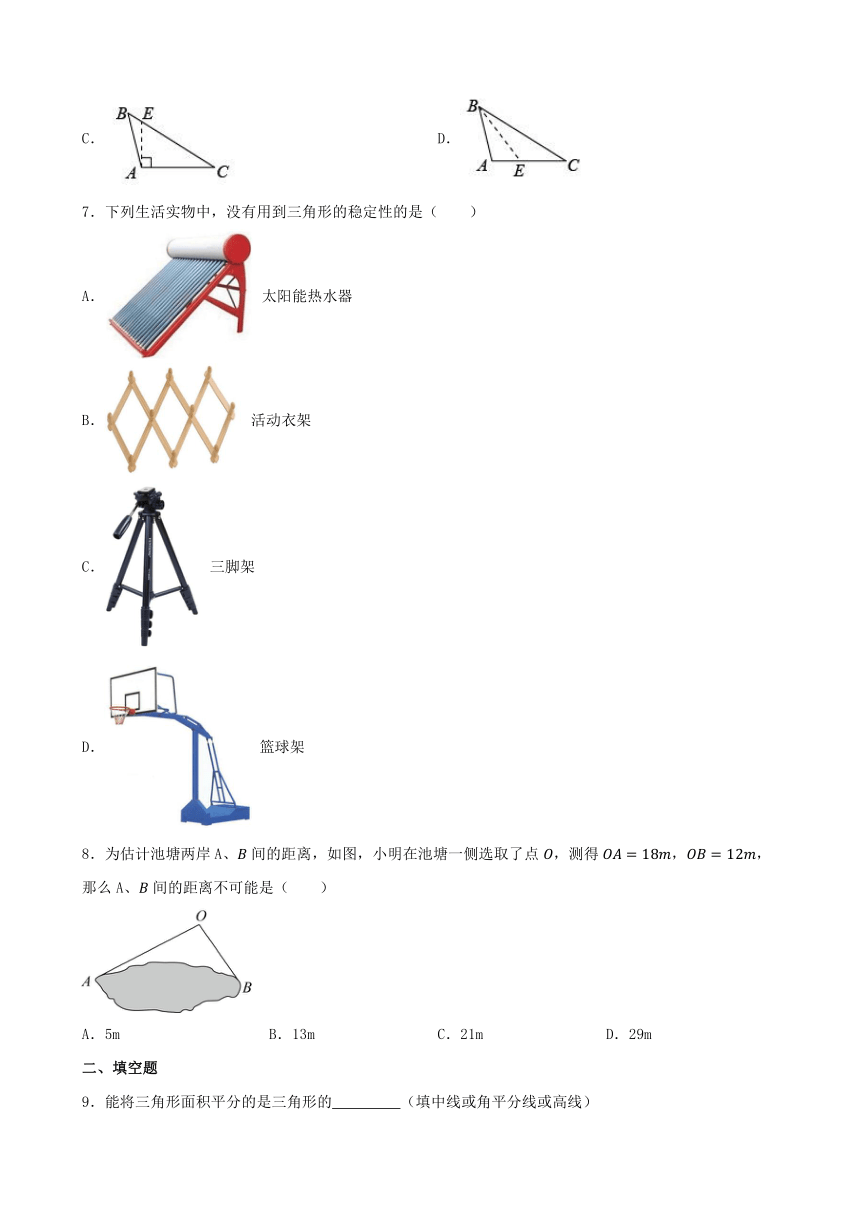
6.下列各图中,正确画出 边上的高的是( )
A. B.
C. D.
7.下列生活实物中,没有用到三角形的稳定性的是( )
A. 太阳能热水器
B. 活动衣架
C. 三脚架
D. 篮球架
8.为估计池塘两岸A、间的距离,如图,小明在池塘一侧选取了点,测得,,那么A、间的距离不可能是( )
A.5m B.13m C.21m D.29m
二、填空题
9.能将三角形面积平分的是三角形的 (填中线或角平分线或高线)
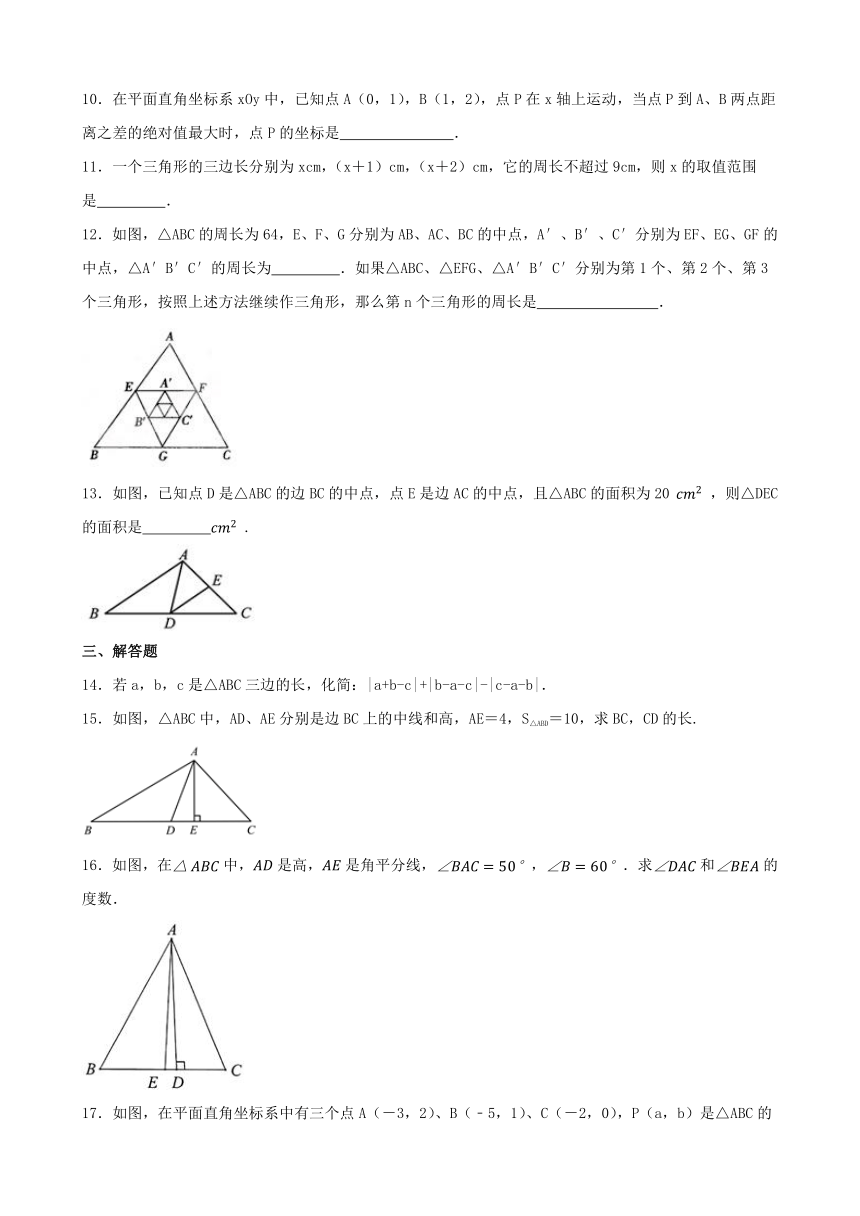
10.在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是 .
11.一个三角形的三边长分别为xcm,(x+1)cm,(x+2)cm,它的周长不超过9cm,则x的取值范围是 .
12.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
13.如图,已知点D是△ABC的边BC的中点,点E是边AC的中点,且△ABC的面积为20 ,则△DEC的面积是 .
三、解答题
14.若a,b,c是△ABC三边的长,化简:|a+b-c|+|b-a-c|-|c-a-b|.
15.如图,△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,求BC,CD的长.
16.如图,在中,是高,是角平分线,,.求和的度数.
17.如图,在平面直角坐标系中有三个点A(-3,2)、B(﹣5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
(1)画出平移后的△A1B1C1,
(2)写出点A1、B1 、C1、的坐标;.
(3)求四边形ACC1A1的面积.
18.如图,中,,为边上的高,平分,且分别交,于点,.求证:.
19.如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点E作EF⊥BC于点F,已知BC=8,△ABC的面积为24,求EF的长.
参考答案
1.B
2.B
3.C
4.D
5.A
6.A
7.B
8.A
9.中线
10.(﹣1,0)
11.112.16;
13.5
14.解:∵ 为△ABC的三边长,
∴ , , ,
∴原式=
= .
15.解:∵在△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,
∴S△ABD= BD AE,
∴BD=5,
∵BD=DC,
∴CD=5,BC=2BD=10.
16.解:
,
;
在中,
,
且是角平分线,
,
,
综上所述:.
17.(1)解:由P(a,b)的对应点P1(a+6,b+2),得到△ABC向右平移6个单位,再向上平移2个单位,得到△A1B1C1,如图,
(2)解:如图所示,A1(3,4)、B1(1,3)、C1(4,2)
(3)解:连接AA1、CC1,
∵ = ×7×2=7, = ×7×2=7,
∴ = + =7+7=14.
18.证明:,
,
为边上的高,
,
,
,
是的平分线,
,
,
,
,
.
19.解:∵AD是BC边上的中线,
∴BD=CD.
又∵△ABC的面积为24,
∴ =12,
又∵E是AD的中点,
∴ =6,
又∵BC=8,EF⊥BC于点F,
∴ BD=CD=4,
∴ ,
,
∴EF=3
一、单选题
1.下列长度的三条线段中,能围成三角形的是( )
A.5cm,6cm,12cm B.3cm,4cm,5cm
C.4cm,6cm,10cm D.3cm,4cm,8cm
2.若三条线段中a=3,b=5,为奇数,那么由a、b、c为边组成的三角形共有( )
A.个 B.个 C.无数多个 D.无法确定
3.如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( )
A.12米 B.10米 C.20米 D.8米
4.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,AD是△ABC的角平分线,则( )
A.∠1=∠BAC B.∠1=∠ABC C.∠1=∠BAC D.∠1=∠ABC
6.下列各图中,正确画出 边上的高的是( )
A. B.
C. D.
7.下列生活实物中,没有用到三角形的稳定性的是( )
A. 太阳能热水器
B. 活动衣架
C. 三脚架
D. 篮球架
8.为估计池塘两岸A、间的距离,如图,小明在池塘一侧选取了点,测得,,那么A、间的距离不可能是( )
A.5m B.13m C.21m D.29m
二、填空题
9.能将三角形面积平分的是三角形的 (填中线或角平分线或高线)
10.在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是 .
11.一个三角形的三边长分别为xcm,(x+1)cm,(x+2)cm,它的周长不超过9cm,则x的取值范围是 .
12.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
13.如图,已知点D是△ABC的边BC的中点,点E是边AC的中点,且△ABC的面积为20 ,则△DEC的面积是 .
三、解答题
14.若a,b,c是△ABC三边的长,化简:|a+b-c|+|b-a-c|-|c-a-b|.
15.如图,△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,求BC,CD的长.
16.如图,在中,是高,是角平分线,,.求和的度数.
17.如图,在平面直角坐标系中有三个点A(-3,2)、B(﹣5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
(1)画出平移后的△A1B1C1,
(2)写出点A1、B1 、C1、的坐标;.
(3)求四边形ACC1A1的面积.
18.如图,中,,为边上的高,平分,且分别交,于点,.求证:.
19.如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点E作EF⊥BC于点F,已知BC=8,△ABC的面积为24,求EF的长.
参考答案
1.B
2.B
3.C
4.D
5.A
6.A
7.B
8.A
9.中线
10.(﹣1,0)
11.1
13.5
14.解:∵ 为△ABC的三边长,
∴ , , ,
∴原式=
= .
15.解:∵在△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,
∴S△ABD= BD AE,
∴BD=5,
∵BD=DC,
∴CD=5,BC=2BD=10.
16.解:
,
;
在中,
,
且是角平分线,
,
,
综上所述:.
17.(1)解:由P(a,b)的对应点P1(a+6,b+2),得到△ABC向右平移6个单位,再向上平移2个单位,得到△A1B1C1,如图,
(2)解:如图所示,A1(3,4)、B1(1,3)、C1(4,2)
(3)解:连接AA1、CC1,
∵ = ×7×2=7, = ×7×2=7,
∴ = + =7+7=14.
18.证明:,
,
为边上的高,
,
,
,
是的平分线,
,
,
,
,
.
19.解:∵AD是BC边上的中线,
∴BD=CD.
又∵△ABC的面积为24,
∴ =12,
又∵E是AD的中点,
∴ =6,
又∵BC=8,EF⊥BC于点F,
∴ BD=CD=4,
∴ ,
,
∴EF=3
