12.3 角的平分线的性质 同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.3 角的平分线的性质 同步练习 2023-2024学年人教版数学八年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 164.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览




文档简介
12.3 角平分线的性质 同步练习 2022-2023学年人教版数学八年级上册
一、单选题
1.点P在∠A0B的平分线上,点P到OA边的距离等于5,点Q是0B边上的任意一点,则下列不符合题意的是( )
A.PQ≤5 B.PQ<5 C.PQ≥5 D.PQ>5
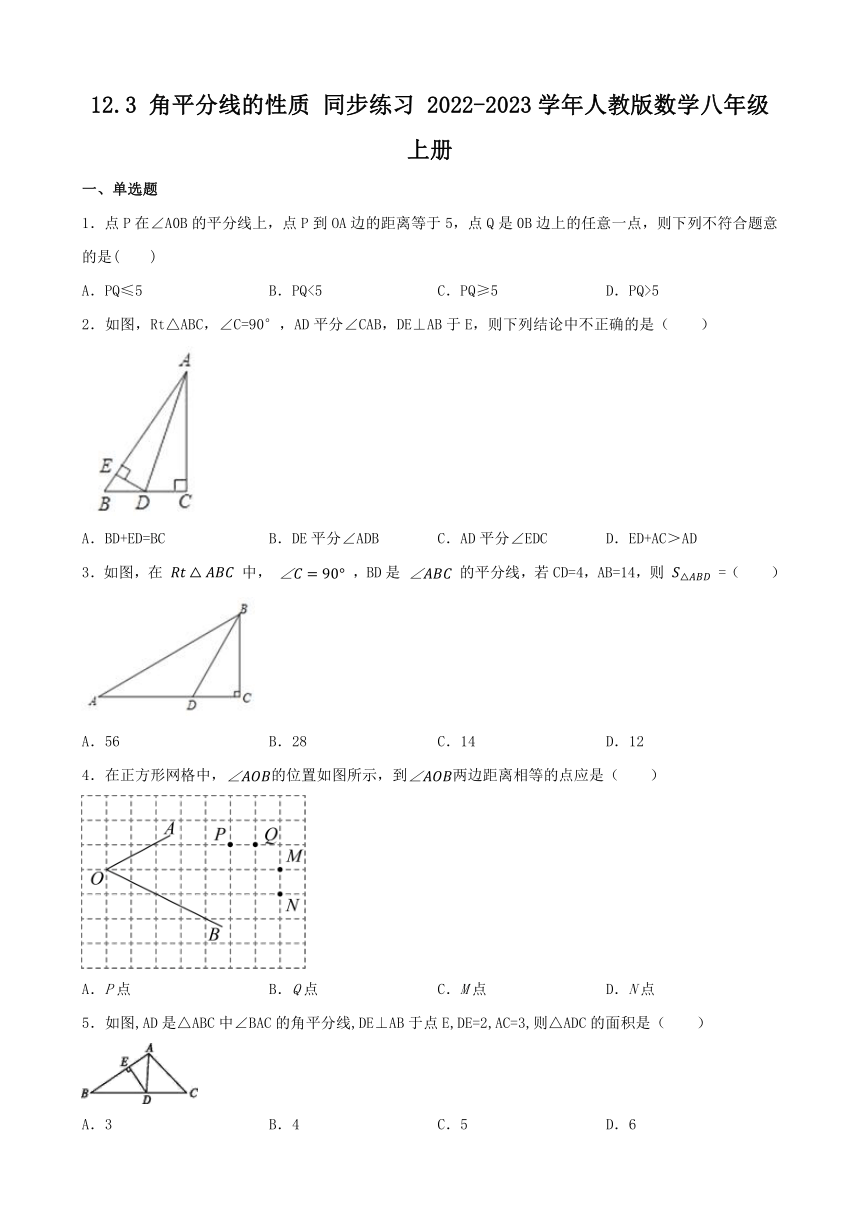
2.如图,Rt△ABC,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中不正确的是( )
A.BD+ED=BC B.DE平分∠ADB C.AD平分∠EDC D.ED+AC>AD
3.如图,在 中, ,BD是 的平分线,若CD=4,AB=14,则 =( )
A.56 B.28 C.14 D.12
4.在正方形网格中,的位置如图所示,到两边距离相等的点应是( )
A.P点 B.Q点 C.M点 D.N点
5.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是( )
A.3 B.4 C.5 D.6
6.如图,Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,连接AE,∠AEB的度数是( )
A.30° B.35° C.45° D.35°
7.如图所示, 为 外部一点, 、 分别在 、 的延长线上,若点 到 、 、 的距离都相等,则关于点 的说法最佳的是( )
A.在 的平分线上
B.在 的平分线上
C.在 的平分线上
D.在 、 、 的平分线上
8.如图,点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上②点P在∠CBE的平分线上③点P在∠BCD的平分线上 ④点P是 ∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A.①②③ B.①②③④ C.②③ D.④
二、填空题
9.如图,PM=PN,∠BOC=20°,则∠AOB= 度.
10.如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点.OE⊥AC于E,OE=2,则点O到AB与CD的距离之和为 .
11.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,CD=3cm,则点D到AB边的距离为 .
13.如图,BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,AB=12,BC=15,△ABC的面积是36,则DE的长是 .
三、解答题
14.如图,BD是△ABC中∠ABC的平分线,于点E ,于点F,若DE=3,AB=7,BC=9,求△ABC的面积.
15.如图,在△ABC中,CM⊥AB于点M,∠ACB的平分线CN交AB于点N,过点N作ND∥AC交BC于点D.若∠A=78°,∠B=50°.
求:①∠CND的度数;②∠MCN的度数.
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
17.如图,在Rt△ABC中,∠C=90°,∠A= ∠ABC,BD平分∠ABC,DE⊥AB,CD=4cm,求AB的长.
18.如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
19.如图,已知: , , 平分 ,
(1)若点 是 的中点,求证: 平分 ;
(2)若 平分 ,猜想 和 的数量关系,并说明理由.
参考答案
1.C
2.B
3.B
4.C
5.A
6.C
7.D
8.B
9.40°
10.4
11.33
12.3cm
13.
14.解:∵BD是△ABC中∠ABC的平分线,于点E ,于点F,
∴DE=DF=3,
∵AB=7,BC=9,
∴=24,
即△ABC的面积是24.
15.解:①∵∠A=78°,∠B=50°,
∴∠ACB=180°-∠A-∠B=52°,
∵CN平分∠ACB,
∴∠ACN=,
∵ND∥AC,
∴∠CND=∠CAN=26°;
②∵CM⊥AB,∠A=78°,
∴∠ACM=90°-∠A=12°,
∴∠MCN=∠ACN-∠ACM=14°.
16.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD= AB×DE+ AC×DF,
∴S△ABC= (AB+AC)×DE,
即 ×(16+12)×DE=28,
解得DE=2(cm).
17.解:∵∠C=90°,∠A= ∠ABC,
∴∠A=30°,∠ABC=60°,
∵BD平分∠ABC,
∴∠DBE=30°,
∴∠A=∠DBE,
∴BD=AD,
∵DE⊥AB,CD=4cm,
∴DE=CD=4cm,
∴AE=BE= DE=4 ,
∴AB=8
18.(1)解:如图所示:
(2)解:DE∥AC
∵DE平分∠BDC,
∴∠BDE= ∠BDC,
∵∠ACD=∠A,∠ACD+∠A=∠BDC,
∴∠A= ∠BDC,
∴∠A=∠BDE,
∴DE∥AC
19.(1)证明:过点 作 ,垂足为 ,如图,
∴ ,
∵ 平分 ,
∴ ,
∵ , ,
∴ ,
∵点 是 的中点,
∴ ,
∴点 在 的平分线上,
∴ 平分 .
(2)解: ,理由如下:
过点 作 ,垂足为 ,如(1)题图,
∵ 平分 , , 平分 ,
∴ , ,
∴
一、单选题
1.点P在∠A0B的平分线上,点P到OA边的距离等于5,点Q是0B边上的任意一点,则下列不符合题意的是( )
A.PQ≤5 B.PQ<5 C.PQ≥5 D.PQ>5
2.如图,Rt△ABC,∠C=90°,AD平分∠CAB,DE⊥AB于E,则下列结论中不正确的是( )
A.BD+ED=BC B.DE平分∠ADB C.AD平分∠EDC D.ED+AC>AD
3.如图,在 中, ,BD是 的平分线,若CD=4,AB=14,则 =( )
A.56 B.28 C.14 D.12
4.在正方形网格中,的位置如图所示,到两边距离相等的点应是( )
A.P点 B.Q点 C.M点 D.N点
5.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是( )
A.3 B.4 C.5 D.6
6.如图,Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,连接AE,∠AEB的度数是( )
A.30° B.35° C.45° D.35°
7.如图所示, 为 外部一点, 、 分别在 、 的延长线上,若点 到 、 、 的距离都相等,则关于点 的说法最佳的是( )
A.在 的平分线上
B.在 的平分线上
C.在 的平分线上
D.在 、 、 的平分线上
8.如图,点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上②点P在∠CBE的平分线上③点P在∠BCD的平分线上 ④点P是 ∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A.①②③ B.①②③④ C.②③ D.④
二、填空题
9.如图,PM=PN,∠BOC=20°,则∠AOB= 度.
10.如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点.OE⊥AC于E,OE=2,则点O到AB与CD的距离之和为 .
11.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,CD=3cm,则点D到AB边的距离为 .
13.如图,BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,AB=12,BC=15,△ABC的面积是36,则DE的长是 .
三、解答题
14.如图,BD是△ABC中∠ABC的平分线,于点E ,于点F,若DE=3,AB=7,BC=9,求△ABC的面积.
15.如图,在△ABC中,CM⊥AB于点M,∠ACB的平分线CN交AB于点N,过点N作ND∥AC交BC于点D.若∠A=78°,∠B=50°.
求:①∠CND的度数;②∠MCN的度数.
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
17.如图,在Rt△ABC中,∠C=90°,∠A= ∠ABC,BD平分∠ABC,DE⊥AB,CD=4cm,求AB的长.
18.如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
19.如图,已知: , , 平分 ,
(1)若点 是 的中点,求证: 平分 ;
(2)若 平分 ,猜想 和 的数量关系,并说明理由.
参考答案
1.C
2.B
3.B
4.C
5.A
6.C
7.D
8.B
9.40°
10.4
11.33
12.3cm
13.
14.解:∵BD是△ABC中∠ABC的平分线,于点E ,于点F,
∴DE=DF=3,
∵AB=7,BC=9,
∴=24,
即△ABC的面积是24.
15.解:①∵∠A=78°,∠B=50°,
∴∠ACB=180°-∠A-∠B=52°,
∵CN平分∠ACB,
∴∠ACN=,
∵ND∥AC,
∴∠CND=∠CAN=26°;
②∵CM⊥AB,∠A=78°,
∴∠ACM=90°-∠A=12°,
∴∠MCN=∠ACN-∠ACM=14°.
16.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD= AB×DE+ AC×DF,
∴S△ABC= (AB+AC)×DE,
即 ×(16+12)×DE=28,
解得DE=2(cm).
17.解:∵∠C=90°,∠A= ∠ABC,
∴∠A=30°,∠ABC=60°,
∵BD平分∠ABC,
∴∠DBE=30°,
∴∠A=∠DBE,
∴BD=AD,
∵DE⊥AB,CD=4cm,
∴DE=CD=4cm,
∴AE=BE= DE=4 ,
∴AB=8
18.(1)解:如图所示:
(2)解:DE∥AC
∵DE平分∠BDC,
∴∠BDE= ∠BDC,
∵∠ACD=∠A,∠ACD+∠A=∠BDC,
∴∠A= ∠BDC,
∴∠A=∠BDE,
∴DE∥AC
19.(1)证明:过点 作 ,垂足为 ,如图,
∴ ,
∵ 平分 ,
∴ ,
∵ , ,
∴ ,
∵点 是 的中点,
∴ ,
∴点 在 的平分线上,
∴ 平分 .
(2)解: ,理由如下:
过点 作 ,垂足为 ,如(1)题图,
∵ 平分 , , 平分 ,
∴ , ,
∴
