第四章 一次函数 检测卷 2023-2024学年北师大版数学八年级上册(无答案)
文档属性
| 名称 | 第四章 一次函数 检测卷 2023-2024学年北师大版数学八年级上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览

文档简介
第四章 一次函数 检测卷
(满分:120分 时间:90分钟)
班级____________ 姓名____________ 学号____________
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列函数中,属于正比例函数的是()
A.y=x2+2 B.y=-2x+1
C.y= D.y=
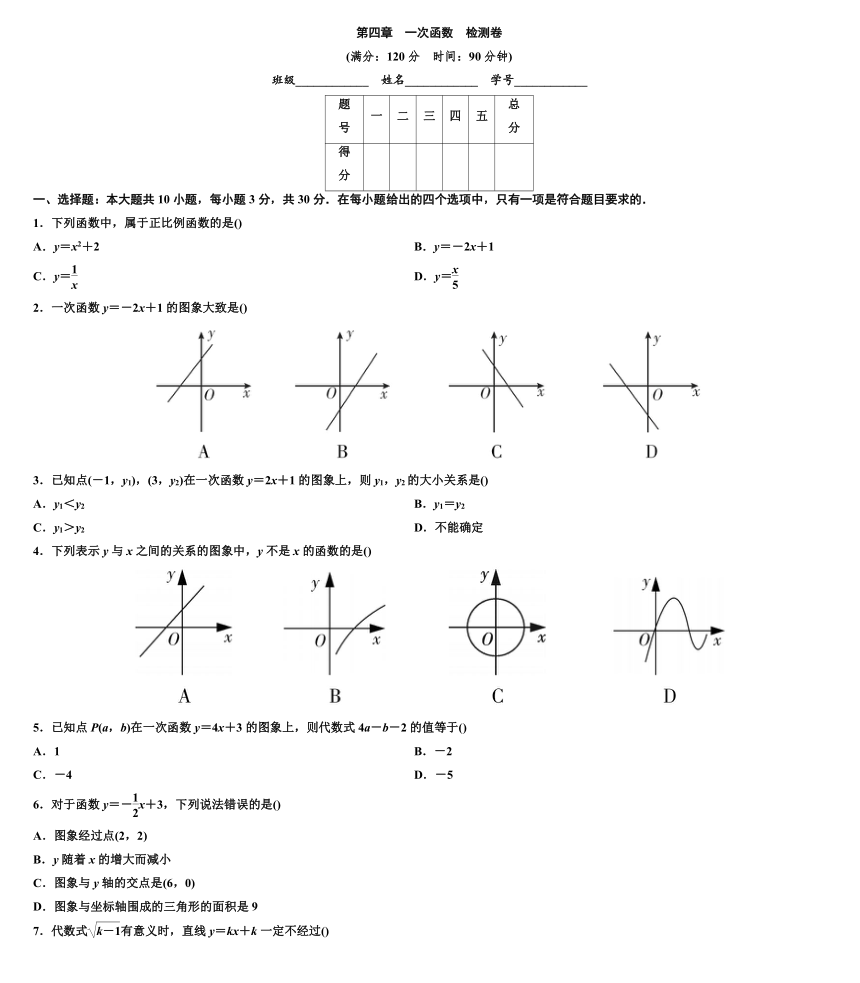
2.一次函数y=-2x+1的图象大致是()
3.已知点(-1,y1),(3,y2)在一次函数y=2x+1的图象上,则y1,y2的大小关系是()
A.y1<y2 B.y1=y2
C.y1>y2 D.不能确定
4.下列表示y与x之间的关系的图象中,y不是x的函数的是()
5.已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a-b-2的值等于()
A.1 B.-2
C.-4 D.-5
6.对于函数y=-x+3,下列说法错误的是()
A.图象经过点(2,2)
B.y随着x的增大而减小
C.图象与y轴的交点是(6,0)
D.图象与坐标轴围成的三角形的面积是9
7.代数式有意义时,直线y=kx+k一定不经过()
A.第一象限 B.第二象限
C.第三象限 D.第四象限
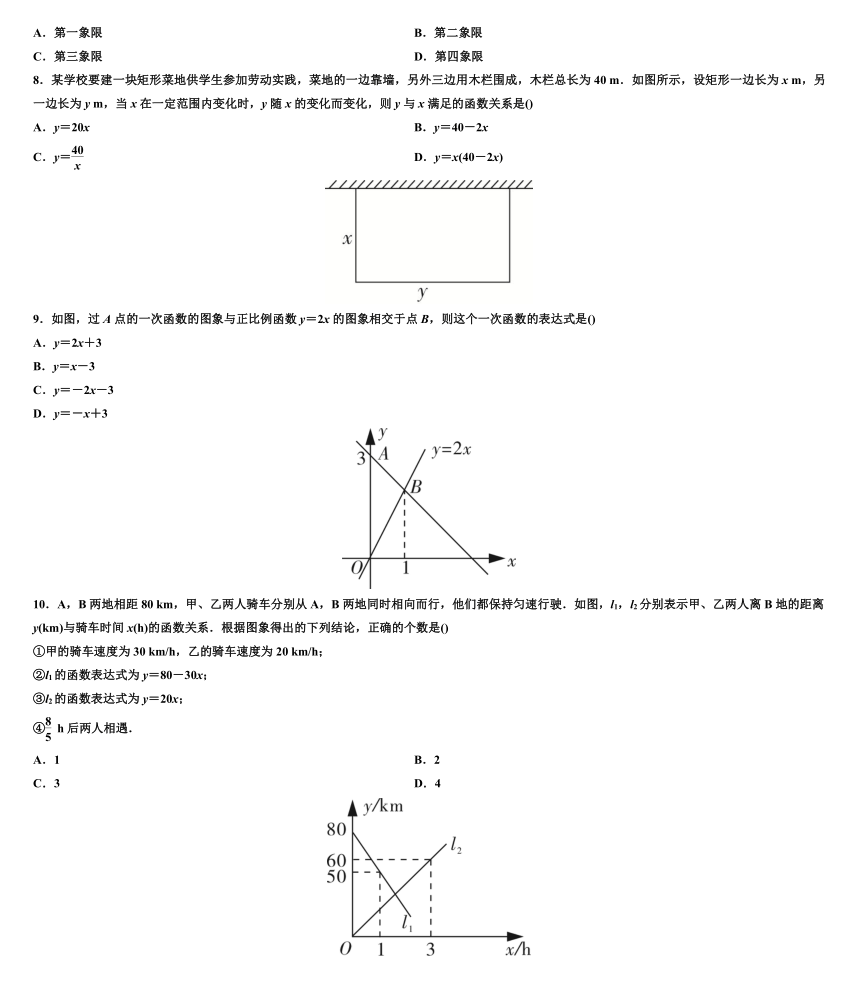
8.某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40 m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是()
A.y=20x B.y=40-2x
C.y= D.y=x(40-2x)
9.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是()
A.y=2x+3
B.y=x-3
C.y=-2x-3
D.y=-x+3
10.A,B两地相距80 km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是()
①甲的骑车速度为30 km/h,乙的骑车速度为20 km/h;
②l1的函数表达式为y=80-30x;
③l2的函数表达式为y=20x;
④ h后两人相遇.
A.1 B.2
C.3 D.4
二、填空题:本大题共5小题,每小题3分,共15分.
11.一次函数y=2x-4与y轴的交点的坐标是.
12.当m时,函数y=(m-3)x-2中y随x的增大而减小.
13. 若函数y=(m-3)x|m-2|+m-1是一次函数,则m的值为.
14.若将直线y=2x-1向上平移3个单位,则所得直线的函数表达式为.
15.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子质量x(kg)与售价y(元)之间的关系如下表:
质量x/kg 1 2 3 …
售价y/元 1.2+0.1 2.4+0.1 3.6+0.1 …
根据表中数据可知,若卖出柚子10 kg,则售价为元.
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.已知正比例函数y=kx的图象过点P(3,-3).
(1)写出这个正比例函数的表达式;
(2)已知点A(a,2)在这个正比例函数的图象上,求a的值.
17.若y-2与x+2成正比例,且x=0时,y=6.
(1)求出y与x之间的函数表达式;
(2)如果点P(m,3)在这个函数的图象上,求m的值.
18.如图,根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=-3的解.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.甲、乙两地打电话需付的电话费y(元)是随时间t(min)的变化而变化的,试根据下表列出的几组数据回答下列问题:
通话时间t/min 1 2 3 4 5 6 …
电话费y/元 0.15 0.30 0.45 0.6 0.75 0.9 …
(1)写出电话费y(元)与通话时间t(min)之间的关系式.
(2)若小明通话10 min,则需付话费多少元?
(3)若小明某次通话后,需付话费4.8元,则小明通话多少分钟?
20.如图,一次函数的图象分别与x轴,y轴交于点A(2,0),B(0,4).
(1)求函数的表达式;
(2)在该一次函数图象上有一点P,到x轴的距离为6,求点P的坐标.
21.探测气球甲从海拔6 m处出发,与此同时,探测气球乙从海拔12 m处出发,图中的l1,l2分别表示甲、乙两个气球所在位置的海拔s(单位:m)与上升时间t(单位:min)之间的关系.
(1)求l1,l2的函数表达式.
(2)探测气球甲从出发点上升到海拔20 m处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.春节临近,某网商紧急备货,但目前缺少大量礼品包装盒,该网商通过调研,发现这种礼品包装盒的来源有两种方案可供选择.
方案一:从纸箱厂订购,购买所需费用y1(单位:元)与礼品盒数x(单位:盒)满足如图所示的函数关系;
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包括租赁机器的费用和生产礼盒的费用)y2(单位:元)与礼品盒数x(单位:盒)满足如图所示的函数关系.
请回答问题:
(1)方案一中礼品盒的单价为元,方案二中礼品盒的单价为元.
(2)请分别求出y1,y2与x的函数关系式.
(3)如何选择方案,才能更省钱?请说明理由.
23.如图,直线y=kx-1与x轴、y轴分别交于点B,C,且OB=2.
(1)求k的值.
(2)若点A是直线y=kx-1上一动点,且点A在第一象限,当△AOB的面积为2时,求点A的坐标.
(3)在(2)的条件下,y轴上是否存在点P,使得△POA是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(满分:120分 时间:90分钟)
班级____________ 姓名____________ 学号____________
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列函数中,属于正比例函数的是()
A.y=x2+2 B.y=-2x+1
C.y= D.y=
2.一次函数y=-2x+1的图象大致是()
3.已知点(-1,y1),(3,y2)在一次函数y=2x+1的图象上,则y1,y2的大小关系是()
A.y1<y2 B.y1=y2
C.y1>y2 D.不能确定
4.下列表示y与x之间的关系的图象中,y不是x的函数的是()
5.已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a-b-2的值等于()
A.1 B.-2
C.-4 D.-5
6.对于函数y=-x+3,下列说法错误的是()
A.图象经过点(2,2)
B.y随着x的增大而减小
C.图象与y轴的交点是(6,0)
D.图象与坐标轴围成的三角形的面积是9
7.代数式有意义时,直线y=kx+k一定不经过()
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40 m.如图所示,设矩形一边长为x m,另一边长为y m,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是()
A.y=20x B.y=40-2x
C.y= D.y=x(40-2x)
9.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是()
A.y=2x+3
B.y=x-3
C.y=-2x-3
D.y=-x+3
10.A,B两地相距80 km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是()
①甲的骑车速度为30 km/h,乙的骑车速度为20 km/h;
②l1的函数表达式为y=80-30x;
③l2的函数表达式为y=20x;
④ h后两人相遇.
A.1 B.2
C.3 D.4
二、填空题:本大题共5小题,每小题3分,共15分.
11.一次函数y=2x-4与y轴的交点的坐标是.
12.当m时,函数y=(m-3)x-2中y随x的增大而减小.
13. 若函数y=(m-3)x|m-2|+m-1是一次函数,则m的值为.
14.若将直线y=2x-1向上平移3个单位,则所得直线的函数表达式为.
15.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子质量x(kg)与售价y(元)之间的关系如下表:
质量x/kg 1 2 3 …
售价y/元 1.2+0.1 2.4+0.1 3.6+0.1 …
根据表中数据可知,若卖出柚子10 kg,则售价为元.
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.已知正比例函数y=kx的图象过点P(3,-3).
(1)写出这个正比例函数的表达式;
(2)已知点A(a,2)在这个正比例函数的图象上,求a的值.
17.若y-2与x+2成正比例,且x=0时,y=6.
(1)求出y与x之间的函数表达式;
(2)如果点P(m,3)在这个函数的图象上,求m的值.
18.如图,根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=-3的解.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.甲、乙两地打电话需付的电话费y(元)是随时间t(min)的变化而变化的,试根据下表列出的几组数据回答下列问题:
通话时间t/min 1 2 3 4 5 6 …
电话费y/元 0.15 0.30 0.45 0.6 0.75 0.9 …
(1)写出电话费y(元)与通话时间t(min)之间的关系式.
(2)若小明通话10 min,则需付话费多少元?
(3)若小明某次通话后,需付话费4.8元,则小明通话多少分钟?
20.如图,一次函数的图象分别与x轴,y轴交于点A(2,0),B(0,4).
(1)求函数的表达式;
(2)在该一次函数图象上有一点P,到x轴的距离为6,求点P的坐标.
21.探测气球甲从海拔6 m处出发,与此同时,探测气球乙从海拔12 m处出发,图中的l1,l2分别表示甲、乙两个气球所在位置的海拔s(单位:m)与上升时间t(单位:min)之间的关系.
(1)求l1,l2的函数表达式.
(2)探测气球甲从出发点上升到海拔20 m处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.春节临近,某网商紧急备货,但目前缺少大量礼品包装盒,该网商通过调研,发现这种礼品包装盒的来源有两种方案可供选择.
方案一:从纸箱厂订购,购买所需费用y1(单位:元)与礼品盒数x(单位:盒)满足如图所示的函数关系;
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包括租赁机器的费用和生产礼盒的费用)y2(单位:元)与礼品盒数x(单位:盒)满足如图所示的函数关系.
请回答问题:
(1)方案一中礼品盒的单价为元,方案二中礼品盒的单价为元.
(2)请分别求出y1,y2与x的函数关系式.
(3)如何选择方案,才能更省钱?请说明理由.
23.如图,直线y=kx-1与x轴、y轴分别交于点B,C,且OB=2.
(1)求k的值.
(2)若点A是直线y=kx-1上一动点,且点A在第一象限,当△AOB的面积为2时,求点A的坐标.
(3)在(2)的条件下,y轴上是否存在点P,使得△POA是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
