北师版九上数学1.1菱形的性质与判定 同步训练(含解析)
文档属性
| 名称 | 北师版九上数学1.1菱形的性质与判定 同步训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 290.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 18:48:44 | ||
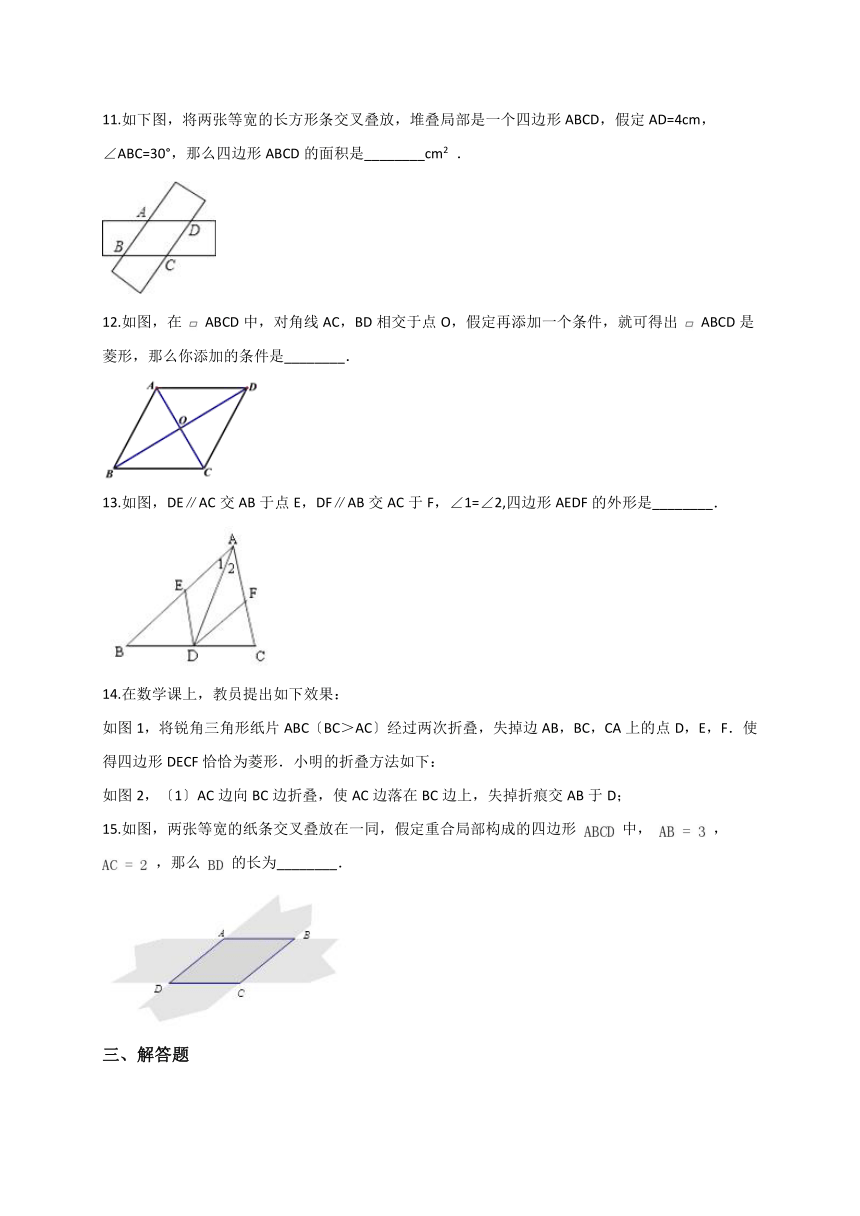
图片预览



文档简介
北师版九上数学1.1菱形的性质与判定同步训练
一、选择题
1.如图,在 ABCD中,对角线 相交于点O,添加以下条件不能判定 ABCD是菱形的只要〔 〕
A. B. C. D.
2.以下命题中正确的选项是〔 〕
A. 对角线相等的四边形是菱形 B. 对角线相互垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形 D. 对角线相互垂直的平行四边形是菱形
3.四边形ABCD是平行四边形,假设要使它成为菱形,那么需求添加的条件是〔 〕
A. ; B. ; C. ; D. .
4.四边形的四边长依次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,那么此四边形一定是〔 〕
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.在平面直角坐标系中,点A〔0,2〕,B〔﹣2 ,0〕,C〔0,﹣2〕,D〔2 ,0〕,那么以这四个点为顶点的四边形ABCD是〔 〕
A. 矩形 B. 菱形 C. 正方形 D. 梯形
6.红丝带是关注艾滋病防治效果的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如下图.红丝带堆叠局部构成的图形是〔 〕
A. 正方形 B. 等腰梯形 C. 菱形 D. 矩形
7.如图,在平面直角坐标系xOy中,点A〔 ,0〕,B〔1,1〕.假定平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,那么正确的平移方法是〔 〕
A. 向左平移1个单位,再向下平移1个单位 B. 向左平移〔 〕个单位,再向上平移1个单位
C. 向右平移 个单位,再向上平移1个单位 D. 向右平移1个单位,再向上平移1个单位
8.如图,是一张平行四边形纸片ABCD,要求应用所学知识将它变成一个菱形,甲、乙两位同窗的作法区分如下:关于甲、乙两人的作法,可判别〔 〕
A. 甲正确,乙错误 B. 甲错误,乙正确 C. 甲、乙均正确 D. 甲、乙均错误
9.如图,以A点为圆心,以相反的长为半径作弧,区分与射线AM,AN交于B,C两点,衔接BC,再区分以B,C为圆心,以相反长〔大于 BC〕为半径作弧,两弧相交于点D,衔接AD,BD,CD.那么以下结论错误的选项是〔 〕
A. AD平分∠MAN B. AD垂直平分BC C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
二、填空题
10.在四边形ABCD中,对角线AC、BD交于点O,从〔1〕AB=CD;〔2〕AB∥CD;〔3〕OA=OC;〔4〕OB=OD;〔5〕AC⊥BD;〔6〕AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形.如〔1〕〔2〕〔5〕 ABCD是菱形,再写出契合要求的两个:________ ABCD是菱形;________ ABCD是菱形.
11.如下图,将两张等宽的长方形条交叉叠放,堆叠局部是一个四边形ABCD,假定AD=4cm,∠ABC=30°,那么四边形ABCD的面积是________cm2 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,假定再添加一个条件,就可得出 ABCD是菱形,那么你添加的条件是________.
13.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的外形是________.
14.在数学课上,教员提出如下效果:
如图1,将锐角三角形纸片ABC〔BC>AC〕经过两次折叠,失掉边AB,BC,CA上的点D,E,F.使得四边形DECF恰恰为菱形.小明的折叠方法如下:
如图2,〔1〕AC边向BC边折叠,使AC边落在BC边上,失掉折痕交AB于D;
15.如图,两张等宽的纸条交叉叠放在一同,假定重合局部构成的四边形 中, , ,那么 的长为________.
三、解答题
16.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,衔接DE.
求证:四边形BCED是菱形.
17.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
18.如图,在 ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC区分相交于点E、F,求证:四边形AECF是菱形.
19.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,假定∠BAD=∠BCD,AM=AN.
求证:四边形ABCD是菱形.
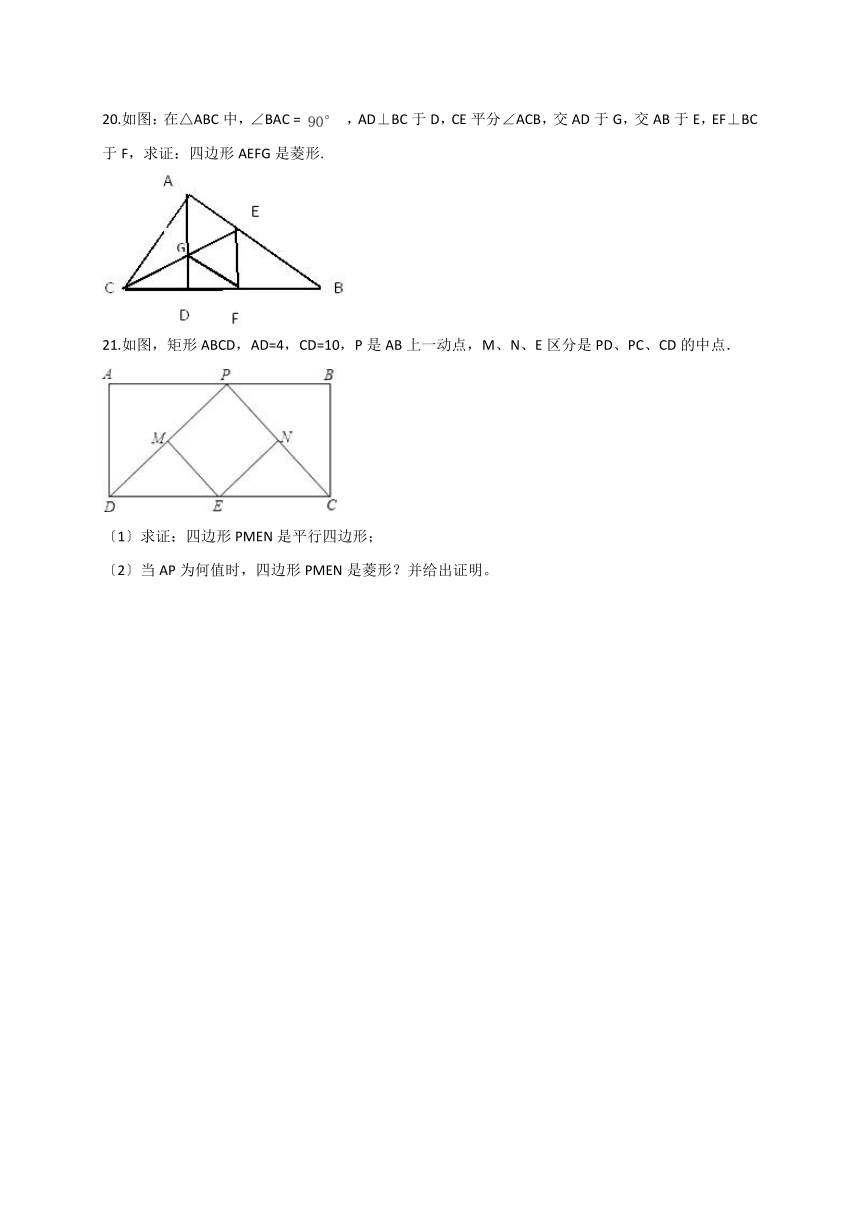
20.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
21.如图,矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E区分是PD、PC、CD的中点.
〔1〕求证:四边形PMEN是平行四边形;
〔2〕当AP为何值时,四边形PMEN是菱形?并给出证明。
答案解析
一、选择题
1.【答案】C
【考点】菱形的判定
【解析】【解答】由于对角线相互垂直的平行四边形是菱形,所以A可以判定 ABCD是菱形;由于一组邻边相等的平行四边形是菱形,所以B可以判定 ABCD是菱形;由于对角线相等的平行四边形是矩形,所以C不可以判定 ABCD是菱形;由于∠1=∠2,OB=OD,所以AB=AD,所以D可以判定 ABCD是菱形,故答案为:C.【剖析】图形曾经是平行四边形了,在此基础上要判别四边形是菱形,只需求添加一个菱形具有的特殊性质,如 :对角线相互垂直,或一组邻边相等,即可,所以,从给的四个四个选项中只需能判定出两特殊性质中的一个即可。
2.【答案】D
【考点】菱形的判定
【解析】【解答】解:在一个平面内,一组邻边相等的平行四边形是菱形。对角线相互垂直的平行四边形是菱形,四条边都相等的四边形是菱形。故答案为:D
【剖析】菱形的判定有:对角线相互垂直的平行四边形是菱形、有一组邻边相等的平行四边形是菱形、对角线相互垂直平分的四边形是菱形、四边相等的四边形是菱形。
3.【答案】B
【考点】菱形的判定
【解析】【解答】解:∵四边形ABCD是平行四边形,
当 时,
平行四边形ABCD是菱形.
∴添加的条件为: .
故答案为:B.
【剖析】依据有一组邻边相等的平行四边形是菱形可求解。
4.【答案】C
【考点】菱形的判定
【解析】【解答】解:整理配方式子a2+b2+c2+d2=ab+bc+cd+ad,
2〔a2+b2+c2+d2〕=2〔ab+bc+cd+ad〕,〕
∴〔a﹣b〕2+〔b﹣c〕2+〔c﹣d〕2+〔a﹣d〕2=0,
由非正数的性质可知:〔a﹣b〕=0,〔b﹣c〕=0,〔c﹣d〕=0,〔a﹣d〕=0,
∴a=b=c=d,
∴四边形一定是菱形,
故答案为:C.
【剖析】将a、b、c、d所满足的等式变形整理可得a=b=c=d,依据菱形的判定可得四边形一定是菱形。
5.【答案】B
【考点】菱形的判定
【解析】【解答】画出草图,求得各边的长,再依据特殊四边形的判定方法判别.在平面直角坐标系中画出图后,可发现这个四边形的对角线相互平分,先判别为平行四边形,对角线还垂直,那么这样的平行四边形应是菱形.【剖析】,依据题意画出草图,求出各边的长,由菱形的判定定理可得结论。
6.【答案】C
【考点】菱形的判定
【解析】【解答】解:过点A作AE⊥BC于E,AF⊥CD于F,
由于两条彩带宽度相反,所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S ABCD=BC AE=CD AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故答案为:C.
【剖析】依据菱形的定义有一组邻边相等的平行四边形是菱形可判别结果。
7.【答案】D
【考点】菱形的判定与性质,坐标与图形变化﹣平移
【解析】【解答】解:过B作射线BC∥OA,在BC上截取BC=OA,那么四边形OACB是平行四边形,
过B作DH⊥x轴于H,
∵B〔1,1〕,
∴OB= ,
∵A〔 ,0〕,
∴C〔1+ ,1〕
∴OA=OB,
∴那么四边形OACB是菱形,
∴平移点A到点C,向右平移1个单位,再向上平移1个单位而失掉,
故答案为:D.
【剖析】过B作射线BC∥OA,在BC上截取BC=OA,过B作DH⊥x轴于H,依据一组对边平行且相等的四边形是平行四边形可得四边形OACB是平行四边形,用勾股定理可求得OB的长,由计算可知OA=OB,且点C的坐标可求解,有一组邻边相等的平行四边形是菱形可得四边形OACB是菱形,依据点C的坐标即可判别平移的方法。
8.【答案】C
【考点】菱形的判定
【解析】【解答】解:如图,
甲的作法正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF〔ASA〕,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
乙的作法正确;
∵AD∥BC,
∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形;
应选:C.
【剖析】首先证明△AOE≌△COF〔ASA〕,可得AE=CF,再依据一组对边平行且相等的四边形是平行四边形可判定判定四边形AECF是平行四 边形,再由AC⊥EF,可依据对角线相互垂直的四边形是菱形判定出AECF是菱形;四边形ABCD是平行四边形,可依据角平分线的定义战争行线的定义,求 得AB=AF,所以四边形ABEF是菱形.
9.【答案】D
【考点】角平分线的性质,作图—基本作图
【解析】【解答】解:A、由作法可得AD平分∠MAN,所以A选项的结论正确;
B、由于AB=AC,DB=DC,所以AD垂直平分BC,所以B选项的结论正确;
C、由于AB=AC,DB=DC,所以∠ABC=∠ACB,∠DBC=∠DCB,那么∠ABD=∠ACD,所以∠MBD=∠NCD,所以C选项的结论正确;
D、BA不一定等于BD,所以四边形ABDC不一定是菱形,所以D选项的结论错误.
应选D.
【剖析】应用基本作图对A停止判别;应用作法失掉AB=AC,DB=DC,那么依据线段垂直平分线的判定方法可对B停止判定;依据等腰三角形的性质失掉∠ABC=∠ACB,∠DBC=∠DCB,那么∠ABD=∠ACD,然后依据邻补角对C停止判定;应用作图可直接对D停止判定.
二、填空题
10.【答案】〔1〕〔2〕〔6〕;〔3〕〔4〕〔5〕或许〔3〕〔4〕〔6〕
【考点】菱形的判定
【解析】【解答】解:菱形的判定方法有三种:
定义:一组邻边相等的平行四边形是菱形;
四边相等;
③对角线相互垂直平分的四边形是菱形.
〔 1 〕〔2〕〔6〕 ABCD是菱形.
先由〔1〕〔2〕得出四边形是平行四边形,
再由〔6〕和〔2〕得出
由等角对等边得
所以平行四边形是菱形.
〔 3 〕〔4〕〔5〕 ABCD是菱形.
由对角线相互平分且垂直的四边形是菱形.
〔 3 〕〔4〕〔6〕 ABCD是菱形.
由〔3〕〔4〕得出四边形是平行四边形,
再由〔6〕得出
由等角对等边得
所以平行四边形是菱形.
故答案为:
【剖析】菱形的判定:对角线相互垂直平分的四边形是菱形、四条边都相等的四边形是菱形依据这些判定即可知四边形ABCD是菱形的有:( 1 ) ( 2 ) ( 6 ) 和 ( 3 ) ( 4 ) ( 5 ) 。
11.【答案】8
【考点】菱形的判定,平行四边形的面积
【解析】【解答】解:∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,
区分作CD,BC边上的高为AE,AF,如下图:
∵两纸条相反,∴纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,∴CD=BC.∴平行四边形ABCD为菱形,
∴AB=AD=4cm,
∵∠ABC=30°,∴AE= AB=2cm,∴S菱形ABCD=BC AE=4×2=8,
故答案为8.
【剖析】区分作CD,BC边上的高为AE,AF,由题意易证四边形ABCD为菱形,解直角三角形ABE可求得AE的长,那么菱形ABCD的面积=BC AE即可求解。
12.【答案】AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA
【考点】菱形的判定
【解析】【解答】解:依据对角线相互垂直的平行四边形是菱形可得,添加的条件可以是:AC⊥BD;
依据四边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC=CD=DA.
故答案是:AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA.
【剖析】答案不独一。依据菱形的判定可添加条件:对角线相互垂直的平行四边形是菱形、有一组邻边相等的平行四边形是菱形、对角线平分一组对角的平行四边形是菱形。
13.【答案】菱形
【考点】菱形的判定
【解析】【解答】解:依据题意,DE∥AC,DF∥AB,
那么四边形AEDF是平行四边形,
又∵AD是△ABC的角平分线,
∴∠EAD=∠DAF=∠ADE,
那么AE=ED,
即四边形AEDF是菱形.
故答案是:菱形.
【剖析】由题意依据两组对边区分平行的四边形是平行四边形可得四边形AEDF是平行四边形,再依据AD是△ABC的角平分线,易证得AE=ED,依据有一组邻边相等的平行四边形是菱形可得四边形AEDF是菱形.
14.【答案】对角线相互垂直平分的四边形是菱形
【考点】菱形的判定
【解析】【解答】解:对角线相互垂直平分的四边形是菱形
【剖析】菱形的判定定理:对角线相互垂直平分的四边形是菱形。依据判定即可求解。
15.【答案】
【考点】菱形的判定与性质
【解析】【解答】解:衔接AC,BD由题意得,
四边形ABCD是菱形,∴AO=1,AC⊥BD.
由勾股定理得, , .
【剖析】衔接AC,BD。由题意易证得四边形ABCD是菱形,由菱形的性质用勾股定理可求得OB的长,那么BD=2OB即可求解。
三、解答题
16.【答案】证明:∵ ≌ ,
∴ ,
在 和 中
,
∴ ≌ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴四边形BCED是菱形.
【考点】菱形的判定
【解析】【剖析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,那么CE=DE,依据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
17.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA
∵四边形ABCD是平行四边形
∴DE∥AF
∴∠DEA=∠EAF
∴∠EAF=∠FEA
∴AF=EF
∴AF=AD=DE=EF
∴四边形ADEF是菱形.
【考点】菱形的判定
【解析】【剖析】由折叠的性质战争行四边形的性质易证AF=AD=DE=EF,依据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
18.【答案】证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF与AC垂直,
∴四边形AECF是菱形
【考点】菱形的判定
【解析】【剖析】由平行四边形的性质结合条件用角边角易证△AOE≌△COF,所以AE=CF,AE∥CF,依据一组对边平行且相等的四边形是平行四边形可得四边形AECF是平行四边形,再依据对角线相互垂直的平行四边形是菱形可得四边形AECF是菱形。
19.【答案】证明:∵AD∥BC,
∴ ,
∵∠BAD=∠BCD,
∴∠B=∠D,
∴四边形ABCD是平行四边形,
∵AM⊥BC,AN⊥DC,
∴
在△ABM和△ADN中,
∴△ABM≌△ADN(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
【考点】菱形的判定
【解析】【剖析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合用角角边易证△ABM≌△ADN,那么可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
20.【答案】证明:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°〔EA⊥CA〕,
∴AE=EF〔角平分线上的点到角两边的距离相等〕,
∵CE=CE,∴由勾股定理得:AC=CF,
∵△ACG和△FCG中
∴△ACG≌△FCG,
∴∠CAD=∠CFG,
∵∠B=∠CAD
∴∠B=∠CFG,
∴GF∥AB,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,
∵AE=EF,
∴平行四边形AEFG是菱形.
【考点】平行四边形的判定,菱形的判定
【解析】【剖析】由用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,依据同垂直于一条直线的两条直线相互平行可得AD∥EF,由两组对边区分平行的四边形是平行四边形可得四边形AEFG是平行四边形,再依据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
21.【答案】〔1〕证明:∵M,E区分为PD,CD的中点,∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形
〔2〕解:当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,∴AP=BP,
在△APD和△BPC中,
AP=BP,∠A=∠B,AD=BC,
∴△APD≌△BPC(SAS),∴PD=PC,
∵M,N,E区分是PD,PC,CD的中点,
∴EN=PM= PD,PN=EM= PC,∴PM=EM=EN=PN,
∴四边形PMEN是菱形.
【考点】平行四边形的判定,菱形的判定,矩形的性质
【解析】【剖析】〔1〕由三角形的中位线定理可得ME∥PC,NE∥PD,依据两组对边区分平行的四边形是平行四边形可得四边形PMEN为平行四边形;
〔2〕由矩形的性质可得∠A=∠B=90°,AD=BC,用边角边易证△APD≌△BPC,可得PD=PC,结合三角形的中位线定理易证PM=EM=EN=PN,依据有四条边相等的四边形是菱形可得四边形PMEN是菱形。
一、选择题
1.如图,在 ABCD中,对角线 相交于点O,添加以下条件不能判定 ABCD是菱形的只要〔 〕
A. B. C. D.
2.以下命题中正确的选项是〔 〕
A. 对角线相等的四边形是菱形 B. 对角线相互垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形 D. 对角线相互垂直的平行四边形是菱形
3.四边形ABCD是平行四边形,假设要使它成为菱形,那么需求添加的条件是〔 〕
A. ; B. ; C. ; D. .
4.四边形的四边长依次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,那么此四边形一定是〔 〕
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.在平面直角坐标系中,点A〔0,2〕,B〔﹣2 ,0〕,C〔0,﹣2〕,D〔2 ,0〕,那么以这四个点为顶点的四边形ABCD是〔 〕
A. 矩形 B. 菱形 C. 正方形 D. 梯形
6.红丝带是关注艾滋病防治效果的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如下图.红丝带堆叠局部构成的图形是〔 〕
A. 正方形 B. 等腰梯形 C. 菱形 D. 矩形
7.如图,在平面直角坐标系xOy中,点A〔 ,0〕,B〔1,1〕.假定平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,那么正确的平移方法是〔 〕
A. 向左平移1个单位,再向下平移1个单位 B. 向左平移〔 〕个单位,再向上平移1个单位
C. 向右平移 个单位,再向上平移1个单位 D. 向右平移1个单位,再向上平移1个单位
8.如图,是一张平行四边形纸片ABCD,要求应用所学知识将它变成一个菱形,甲、乙两位同窗的作法区分如下:关于甲、乙两人的作法,可判别〔 〕
A. 甲正确,乙错误 B. 甲错误,乙正确 C. 甲、乙均正确 D. 甲、乙均错误
9.如图,以A点为圆心,以相反的长为半径作弧,区分与射线AM,AN交于B,C两点,衔接BC,再区分以B,C为圆心,以相反长〔大于 BC〕为半径作弧,两弧相交于点D,衔接AD,BD,CD.那么以下结论错误的选项是〔 〕
A. AD平分∠MAN B. AD垂直平分BC C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
二、填空题
10.在四边形ABCD中,对角线AC、BD交于点O,从〔1〕AB=CD;〔2〕AB∥CD;〔3〕OA=OC;〔4〕OB=OD;〔5〕AC⊥BD;〔6〕AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形.如〔1〕〔2〕〔5〕 ABCD是菱形,再写出契合要求的两个:________ ABCD是菱形;________ ABCD是菱形.
11.如下图,将两张等宽的长方形条交叉叠放,堆叠局部是一个四边形ABCD,假定AD=4cm,∠ABC=30°,那么四边形ABCD的面积是________cm2 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,假定再添加一个条件,就可得出 ABCD是菱形,那么你添加的条件是________.
13.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的外形是________.
14.在数学课上,教员提出如下效果:
如图1,将锐角三角形纸片ABC〔BC>AC〕经过两次折叠,失掉边AB,BC,CA上的点D,E,F.使得四边形DECF恰恰为菱形.小明的折叠方法如下:
如图2,〔1〕AC边向BC边折叠,使AC边落在BC边上,失掉折痕交AB于D;
15.如图,两张等宽的纸条交叉叠放在一同,假定重合局部构成的四边形 中, , ,那么 的长为________.
三、解答题
16.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,衔接DE.
求证:四边形BCED是菱形.
17.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
18.如图,在 ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC区分相交于点E、F,求证:四边形AECF是菱形.
19.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,假定∠BAD=∠BCD,AM=AN.
求证:四边形ABCD是菱形.
20.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
21.如图,矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E区分是PD、PC、CD的中点.
〔1〕求证:四边形PMEN是平行四边形;
〔2〕当AP为何值时,四边形PMEN是菱形?并给出证明。
答案解析
一、选择题
1.【答案】C
【考点】菱形的判定
【解析】【解答】由于对角线相互垂直的平行四边形是菱形,所以A可以判定 ABCD是菱形;由于一组邻边相等的平行四边形是菱形,所以B可以判定 ABCD是菱形;由于对角线相等的平行四边形是矩形,所以C不可以判定 ABCD是菱形;由于∠1=∠2,OB=OD,所以AB=AD,所以D可以判定 ABCD是菱形,故答案为:C.【剖析】图形曾经是平行四边形了,在此基础上要判别四边形是菱形,只需求添加一个菱形具有的特殊性质,如 :对角线相互垂直,或一组邻边相等,即可,所以,从给的四个四个选项中只需能判定出两特殊性质中的一个即可。
2.【答案】D
【考点】菱形的判定
【解析】【解答】解:在一个平面内,一组邻边相等的平行四边形是菱形。对角线相互垂直的平行四边形是菱形,四条边都相等的四边形是菱形。故答案为:D
【剖析】菱形的判定有:对角线相互垂直的平行四边形是菱形、有一组邻边相等的平行四边形是菱形、对角线相互垂直平分的四边形是菱形、四边相等的四边形是菱形。
3.【答案】B
【考点】菱形的判定
【解析】【解答】解:∵四边形ABCD是平行四边形,
当 时,
平行四边形ABCD是菱形.
∴添加的条件为: .
故答案为:B.
【剖析】依据有一组邻边相等的平行四边形是菱形可求解。
4.【答案】C
【考点】菱形的判定
【解析】【解答】解:整理配方式子a2+b2+c2+d2=ab+bc+cd+ad,
2〔a2+b2+c2+d2〕=2〔ab+bc+cd+ad〕,〕
∴〔a﹣b〕2+〔b﹣c〕2+〔c﹣d〕2+〔a﹣d〕2=0,
由非正数的性质可知:〔a﹣b〕=0,〔b﹣c〕=0,〔c﹣d〕=0,〔a﹣d〕=0,
∴a=b=c=d,
∴四边形一定是菱形,
故答案为:C.
【剖析】将a、b、c、d所满足的等式变形整理可得a=b=c=d,依据菱形的判定可得四边形一定是菱形。
5.【答案】B
【考点】菱形的判定
【解析】【解答】画出草图,求得各边的长,再依据特殊四边形的判定方法判别.在平面直角坐标系中画出图后,可发现这个四边形的对角线相互平分,先判别为平行四边形,对角线还垂直,那么这样的平行四边形应是菱形.【剖析】,依据题意画出草图,求出各边的长,由菱形的判定定理可得结论。
6.【答案】C
【考点】菱形的判定
【解析】【解答】解:过点A作AE⊥BC于E,AF⊥CD于F,
由于两条彩带宽度相反,所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S ABCD=BC AE=CD AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故答案为:C.
【剖析】依据菱形的定义有一组邻边相等的平行四边形是菱形可判别结果。
7.【答案】D
【考点】菱形的判定与性质,坐标与图形变化﹣平移
【解析】【解答】解:过B作射线BC∥OA,在BC上截取BC=OA,那么四边形OACB是平行四边形,
过B作DH⊥x轴于H,
∵B〔1,1〕,
∴OB= ,
∵A〔 ,0〕,
∴C〔1+ ,1〕
∴OA=OB,
∴那么四边形OACB是菱形,
∴平移点A到点C,向右平移1个单位,再向上平移1个单位而失掉,
故答案为:D.
【剖析】过B作射线BC∥OA,在BC上截取BC=OA,过B作DH⊥x轴于H,依据一组对边平行且相等的四边形是平行四边形可得四边形OACB是平行四边形,用勾股定理可求得OB的长,由计算可知OA=OB,且点C的坐标可求解,有一组邻边相等的平行四边形是菱形可得四边形OACB是菱形,依据点C的坐标即可判别平移的方法。
8.【答案】C
【考点】菱形的判定
【解析】【解答】解:如图,
甲的作法正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF〔ASA〕,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
乙的作法正确;
∵AD∥BC,
∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形;
应选:C.
【剖析】首先证明△AOE≌△COF〔ASA〕,可得AE=CF,再依据一组对边平行且相等的四边形是平行四边形可判定判定四边形AECF是平行四 边形,再由AC⊥EF,可依据对角线相互垂直的四边形是菱形判定出AECF是菱形;四边形ABCD是平行四边形,可依据角平分线的定义战争行线的定义,求 得AB=AF,所以四边形ABEF是菱形.
9.【答案】D
【考点】角平分线的性质,作图—基本作图
【解析】【解答】解:A、由作法可得AD平分∠MAN,所以A选项的结论正确;
B、由于AB=AC,DB=DC,所以AD垂直平分BC,所以B选项的结论正确;
C、由于AB=AC,DB=DC,所以∠ABC=∠ACB,∠DBC=∠DCB,那么∠ABD=∠ACD,所以∠MBD=∠NCD,所以C选项的结论正确;
D、BA不一定等于BD,所以四边形ABDC不一定是菱形,所以D选项的结论错误.
应选D.
【剖析】应用基本作图对A停止判别;应用作法失掉AB=AC,DB=DC,那么依据线段垂直平分线的判定方法可对B停止判定;依据等腰三角形的性质失掉∠ABC=∠ACB,∠DBC=∠DCB,那么∠ABD=∠ACD,然后依据邻补角对C停止判定;应用作图可直接对D停止判定.
二、填空题
10.【答案】〔1〕〔2〕〔6〕;〔3〕〔4〕〔5〕或许〔3〕〔4〕〔6〕
【考点】菱形的判定
【解析】【解答】解:菱形的判定方法有三种:
定义:一组邻边相等的平行四边形是菱形;
四边相等;
③对角线相互垂直平分的四边形是菱形.
〔 1 〕〔2〕〔6〕 ABCD是菱形.
先由〔1〕〔2〕得出四边形是平行四边形,
再由〔6〕和〔2〕得出
由等角对等边得
所以平行四边形是菱形.
〔 3 〕〔4〕〔5〕 ABCD是菱形.
由对角线相互平分且垂直的四边形是菱形.
〔 3 〕〔4〕〔6〕 ABCD是菱形.
由〔3〕〔4〕得出四边形是平行四边形,
再由〔6〕得出
由等角对等边得
所以平行四边形是菱形.
故答案为:
【剖析】菱形的判定:对角线相互垂直平分的四边形是菱形、四条边都相等的四边形是菱形依据这些判定即可知四边形ABCD是菱形的有:( 1 ) ( 2 ) ( 6 ) 和 ( 3 ) ( 4 ) ( 5 ) 。
11.【答案】8
【考点】菱形的判定,平行四边形的面积
【解析】【解答】解:∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,
区分作CD,BC边上的高为AE,AF,如下图:
∵两纸条相反,∴纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,∴CD=BC.∴平行四边形ABCD为菱形,
∴AB=AD=4cm,
∵∠ABC=30°,∴AE= AB=2cm,∴S菱形ABCD=BC AE=4×2=8,
故答案为8.
【剖析】区分作CD,BC边上的高为AE,AF,由题意易证四边形ABCD为菱形,解直角三角形ABE可求得AE的长,那么菱形ABCD的面积=BC AE即可求解。
12.【答案】AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA
【考点】菱形的判定
【解析】【解答】解:依据对角线相互垂直的平行四边形是菱形可得,添加的条件可以是:AC⊥BD;
依据四边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC=CD=DA.
故答案是:AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA.
【剖析】答案不独一。依据菱形的判定可添加条件:对角线相互垂直的平行四边形是菱形、有一组邻边相等的平行四边形是菱形、对角线平分一组对角的平行四边形是菱形。
13.【答案】菱形
【考点】菱形的判定
【解析】【解答】解:依据题意,DE∥AC,DF∥AB,
那么四边形AEDF是平行四边形,
又∵AD是△ABC的角平分线,
∴∠EAD=∠DAF=∠ADE,
那么AE=ED,
即四边形AEDF是菱形.
故答案是:菱形.
【剖析】由题意依据两组对边区分平行的四边形是平行四边形可得四边形AEDF是平行四边形,再依据AD是△ABC的角平分线,易证得AE=ED,依据有一组邻边相等的平行四边形是菱形可得四边形AEDF是菱形.
14.【答案】对角线相互垂直平分的四边形是菱形
【考点】菱形的判定
【解析】【解答】解:对角线相互垂直平分的四边形是菱形
【剖析】菱形的判定定理:对角线相互垂直平分的四边形是菱形。依据判定即可求解。
15.【答案】
【考点】菱形的判定与性质
【解析】【解答】解:衔接AC,BD由题意得,
四边形ABCD是菱形,∴AO=1,AC⊥BD.
由勾股定理得, , .
【剖析】衔接AC,BD。由题意易证得四边形ABCD是菱形,由菱形的性质用勾股定理可求得OB的长,那么BD=2OB即可求解。
三、解答题
16.【答案】证明:∵ ≌ ,
∴ ,
在 和 中
,
∴ ≌ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴四边形BCED是菱形.
【考点】菱形的判定
【解析】【剖析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,那么CE=DE,依据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
17.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA
∵四边形ABCD是平行四边形
∴DE∥AF
∴∠DEA=∠EAF
∴∠EAF=∠FEA
∴AF=EF
∴AF=AD=DE=EF
∴四边形ADEF是菱形.
【考点】菱形的判定
【解析】【剖析】由折叠的性质战争行四边形的性质易证AF=AD=DE=EF,依据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
18.【答案】证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF与AC垂直,
∴四边形AECF是菱形
【考点】菱形的判定
【解析】【剖析】由平行四边形的性质结合条件用角边角易证△AOE≌△COF,所以AE=CF,AE∥CF,依据一组对边平行且相等的四边形是平行四边形可得四边形AECF是平行四边形,再依据对角线相互垂直的平行四边形是菱形可得四边形AECF是菱形。
19.【答案】证明:∵AD∥BC,
∴ ,
∵∠BAD=∠BCD,
∴∠B=∠D,
∴四边形ABCD是平行四边形,
∵AM⊥BC,AN⊥DC,
∴
在△ABM和△ADN中,
∴△ABM≌△ADN(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
【考点】菱形的判定
【解析】【剖析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合用角角边易证△ABM≌△ADN,那么可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
20.【答案】证明:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°〔EA⊥CA〕,
∴AE=EF〔角平分线上的点到角两边的距离相等〕,
∵CE=CE,∴由勾股定理得:AC=CF,
∵△ACG和△FCG中
∴△ACG≌△FCG,
∴∠CAD=∠CFG,
∵∠B=∠CAD
∴∠B=∠CFG,
∴GF∥AB,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,
∵AE=EF,
∴平行四边形AEFG是菱形.
【考点】平行四边形的判定,菱形的判定
【解析】【剖析】由用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,依据同垂直于一条直线的两条直线相互平行可得AD∥EF,由两组对边区分平行的四边形是平行四边形可得四边形AEFG是平行四边形,再依据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
21.【答案】〔1〕证明:∵M,E区分为PD,CD的中点,∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形
〔2〕解:当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,∴AP=BP,
在△APD和△BPC中,
AP=BP,∠A=∠B,AD=BC,
∴△APD≌△BPC(SAS),∴PD=PC,
∵M,N,E区分是PD,PC,CD的中点,
∴EN=PM= PD,PN=EM= PC,∴PM=EM=EN=PN,
∴四边形PMEN是菱形.
【考点】平行四边形的判定,菱形的判定,矩形的性质
【解析】【剖析】〔1〕由三角形的中位线定理可得ME∥PC,NE∥PD,依据两组对边区分平行的四边形是平行四边形可得四边形PMEN为平行四边形;
〔2〕由矩形的性质可得∠A=∠B=90°,AD=BC,用边角边易证△APD≌△BPC,可得PD=PC,结合三角形的中位线定理易证PM=EM=EN=PN,依据有四条边相等的四边形是菱形可得四边形PMEN是菱形。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
