14.3平方差公式 教学设计 人教版八年级数学上册
文档属性
| 名称 | 14.3平方差公式 教学设计 人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览

文档简介
平方差公式
一、教材分析
<<平方差公式>>是多项式乘以多项式学习之后的再次提升,在内容上是由多项式乘多项式而得到的,同时又为下一节课打下了基础,环环相扣,层层递进。是从一般到特殊的认知规律的典型范例,通过这节课的学习,可以培养学生探索与归纳能力,体会到从简单到复杂,从特殊到一般和转化等重要的思想方法。因此,本节课起着承上启下的作用,并且由于是初中阶段的第一个公式,所以在初中阶段的教学中也具有重要地位。
二、学情分析
学生已熟练掌握了整式乘法,但是在用平方差公式运算时,由于八年级的学生成绩参差不齐,两极分化严重,所以常常会出现找不准公式中的a和b等诸多问题。因此,教学中要引导学生分析公式的结构特征,并运用变式训练揭示公式的本质特征,加深学生对公式的理解和应用。
三、教学目标
1、知识与技能:
(1)经历探索平方差公式的过程。
(2)会推导平方差公式,并能运用公式进行简单运算。
2、过程与方法:
(1)在探索平方差公式的过程中,培养符号感和推理能力。
(2)培养学生观察、归纳、概括的能力。
3、情感态度与价值观:
让学生经历“特殊—一般—特殊”(即:特例─归纳─猜想─验证─实际应用)这一数学活动过程,积累数学活动的经验,同时体会数学的简洁美和数形结合的思想方法。培养他们的合情推理和归纳的能力以及在解决问题过程中与他人合作交流的意识。
四、教学重点和难点
重点:体会公式的发现和推导过程,理解公式的本质和结构特征,能用自己的语言说明公式及其特点;并会运用公式进行简单的计算。
难点:理解公式中字母的广泛含义,并灵活运用公式,把公式中的结构特征与实际问题联系起来。
五、教学方法
启发式教学法、探究教学法。
六、教学环境及资源准备
教材,PPT,多媒体
教学过程设计
讲课总时间:40分钟
教学过程 具体教学过程 师生互动 设计意图
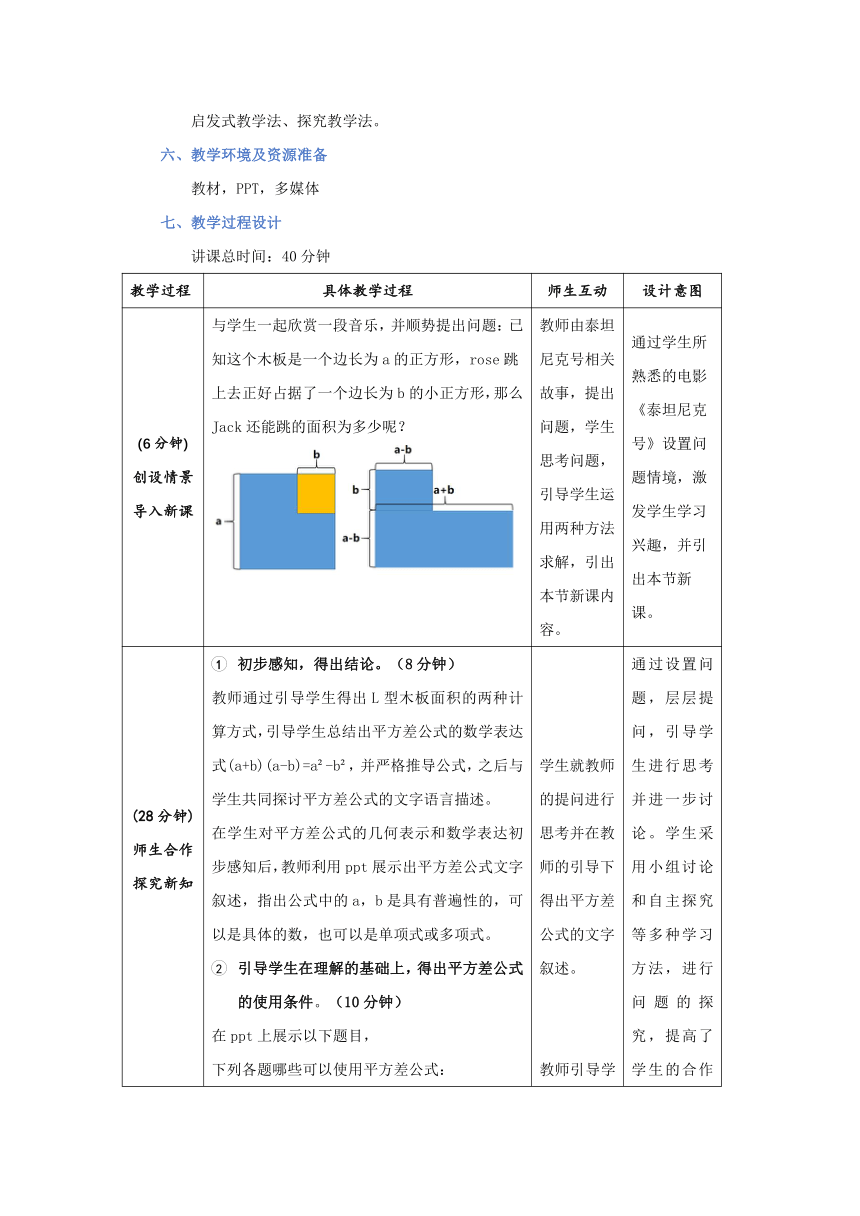
(6分钟) 创设情景导入新课 与学生一起欣赏一段音乐,并顺势提出问题:已知这个木板是一个边长为a的正方形,rose跳上去正好占据了一个边长为b的小正方形,那么Jack还能跳的面积为多少呢? 教师由泰坦尼克号相关故事,提出问题,学生思考问题,引导学生运用两种方法求解,引出本节新课内容。 通过学生所熟悉的电影《泰坦尼克号》设置问题情境,激发学生学习兴趣,并引出本节新课。
(28分钟) 师生合作探究新知 初步感知,得出结论。(8分钟) 教师通过引导学生得出L型木板面积的两种计算方式,引导学生总结出平方差公式的数学表达式(a+b)(a-b)=a -b ,并严格推导公式,之后与学生共同探讨平方差公式的文字语言描述。 在学生对平方差公式的几何表示和数学表达初步感知后,教师利用ppt展示出平方差公式文字叙述,指出公式中的a,b是具有普遍性的,可以是具体的数,也可以是单项式或多项式。 引导学生在理解的基础上,得出平方差公式的使用条件。(10分钟) 在ppt上展示以下题目, 下列各题哪些可以使用平方差公式: (1) (-a+b)(a+b) (2) (a-b)(b+a) (3) (a+b)(-a-b) (4) (-b-a)(b-a) (5) (-b+a)(-a-b) 教师组织学生梳理和总结得出,平方差公式的使用条件:两个多项式中有一项完全相同,另一项互为相反数(一同一反)对于变形的平方差公式,当符号或位置变化,运用同前异后法。 例题讲解,加深学生理解(10分钟) 例1、 (1) (-x-y) (y-x) (2) (3+a) (-3+a) 抽学生上台做题,共同判断正误,并进行点评,给予适当表扬。 紧接着提出平方差公式在符号或位置不同以外,还可能存在系数或指数不同的情况,给出以下例题,总结出人坚不拆法。 例2、 (1) (3x+2) (3x-2) (2) (3a +b3) (3a -b3) 学生就教师的提问进行思考并在教师的引导下得出平方差公式的文字叙述。 教师引导学生通过自主探究,认识到:使用条件是两个多项式中有一项完全相同,另一项互为相反数。(一同一反)并总结出同前异后法。 例1抽学生上讲台做,其余同学自行思考,教师进行讲解并规范书写。 例2教师与学生共同解决问题,并总结出人坚不拆法。 通过设置问题,层层提问,引导学生进行思考并进一步讨论。学生采用小组讨论和自主探究等多种学习方法,进行问题的探究,提高了学生的合作交流、语言表达能力。 首先是通过5个式子,观察得出使用条件,进而得出招式一同前异后。 例1的设计是为了及时巩固学生对同前异后法的理解,了解学生的掌握情况。 例2的设计是针对于系数或指数发生变化的情况,指出了易错点,引出人坚不拆法。
( 4分钟) 课堂练习 1.下列各式能用平方差公式计算的是( ). A. (3a+b)(a-b) B. (-3a-b)(-3a+b) C. (3a+b)(-3a-b) D. (-3a+b)(3a-b) 2.(-4a-1)与(4a-1)的积等于( ). A. -1+16a2 B. -1-8a2 C. 1-4a2 D. 1-16a2 学生们自主思考,得出答案。教师抽学生回答,针对学生出现的问题给予适当的说明。 通过设置适当的练习题,可以加深学生对平方差公式使用条件和变形情况使用方法的理解,巩固知识。
(2分钟) 课堂小结 教师引导学生从知识、能力或情感等方面畅谈本节课的收获,针对学生的回答,采用多种方式进行评价并总结。通过本节课的学习,我们学到了以下知识: 平方差公式(a+b)(a-b)=a -b 两数和与这两数的差的积,等于它们的平方差 2、使用条件:两个多项式中有一项完全相同,另一项互为相反数 3、变形情况: 符号或位置变化——同前异后 系数或指数变化——人坚不拆法 学生们畅所欲言,分享本节课的收获。教师加以总结,进一步加深学生对公式的理解。 通过小结,让学生进一步巩固本节所学内容,并能够灵活运用。
作业布置 课本P112 习题14.2 第1题(必做) 第5题(选做) 通过分层设置课后作业,考虑到学生的不同基础,使学生更好的掌握知识。
板书设计
§14.2.1平方差公式 1.平方差公式 (a+b)(a-b)=a -b 和 差 平方差 2.使用条件:一同一反 3.变形: (1)同前异后 (2)人坚不拆法 PPT 演算板书
教学反思
本节课采用情景-探究的方式,以猜想、实验、论证为主要探究方式,得出平方差公式,应用逆向思维的方向,演绎出平方差公式,对公式的应用首先提醒学生要注意其特征,其次要做好式子的变形,把问题转化成能够应用公式的方面上来,应用公式法因式分解的过程,实际上就是转化和化归的过程。在解决认识平方差公式的结构时候,重点突出学生自我思想的形成,能够充分地不公式用自己的语言来叙述,在整个教学设计中,教师只作为了一个点拨者和引路人。然后应用有梯度的典型例题加以巩固,在学生头脑中形成一个清晰完整的数学模型,使学生在今后的练习中游刃有余。
不足之处:
教学中时间把握还是不足,在设计的题目中不怎么合理,应按题目的难度从易到难。
有些题目的归纳可放手给学生讨论后由学生说出,而不是教师代替。小组评价做的不够,没有足够的小组的活动,没有小组的竞赛。教学语言还太随意,数学的语言应该严谨。在语调上应该有所变化。
一、教材分析
<<平方差公式>>是多项式乘以多项式学习之后的再次提升,在内容上是由多项式乘多项式而得到的,同时又为下一节课打下了基础,环环相扣,层层递进。是从一般到特殊的认知规律的典型范例,通过这节课的学习,可以培养学生探索与归纳能力,体会到从简单到复杂,从特殊到一般和转化等重要的思想方法。因此,本节课起着承上启下的作用,并且由于是初中阶段的第一个公式,所以在初中阶段的教学中也具有重要地位。
二、学情分析
学生已熟练掌握了整式乘法,但是在用平方差公式运算时,由于八年级的学生成绩参差不齐,两极分化严重,所以常常会出现找不准公式中的a和b等诸多问题。因此,教学中要引导学生分析公式的结构特征,并运用变式训练揭示公式的本质特征,加深学生对公式的理解和应用。
三、教学目标
1、知识与技能:
(1)经历探索平方差公式的过程。
(2)会推导平方差公式,并能运用公式进行简单运算。
2、过程与方法:
(1)在探索平方差公式的过程中,培养符号感和推理能力。
(2)培养学生观察、归纳、概括的能力。
3、情感态度与价值观:
让学生经历“特殊—一般—特殊”(即:特例─归纳─猜想─验证─实际应用)这一数学活动过程,积累数学活动的经验,同时体会数学的简洁美和数形结合的思想方法。培养他们的合情推理和归纳的能力以及在解决问题过程中与他人合作交流的意识。
四、教学重点和难点
重点:体会公式的发现和推导过程,理解公式的本质和结构特征,能用自己的语言说明公式及其特点;并会运用公式进行简单的计算。
难点:理解公式中字母的广泛含义,并灵活运用公式,把公式中的结构特征与实际问题联系起来。
五、教学方法
启发式教学法、探究教学法。
六、教学环境及资源准备
教材,PPT,多媒体
教学过程设计
讲课总时间:40分钟
教学过程 具体教学过程 师生互动 设计意图
(6分钟) 创设情景导入新课 与学生一起欣赏一段音乐,并顺势提出问题:已知这个木板是一个边长为a的正方形,rose跳上去正好占据了一个边长为b的小正方形,那么Jack还能跳的面积为多少呢? 教师由泰坦尼克号相关故事,提出问题,学生思考问题,引导学生运用两种方法求解,引出本节新课内容。 通过学生所熟悉的电影《泰坦尼克号》设置问题情境,激发学生学习兴趣,并引出本节新课。
(28分钟) 师生合作探究新知 初步感知,得出结论。(8分钟) 教师通过引导学生得出L型木板面积的两种计算方式,引导学生总结出平方差公式的数学表达式(a+b)(a-b)=a -b ,并严格推导公式,之后与学生共同探讨平方差公式的文字语言描述。 在学生对平方差公式的几何表示和数学表达初步感知后,教师利用ppt展示出平方差公式文字叙述,指出公式中的a,b是具有普遍性的,可以是具体的数,也可以是单项式或多项式。 引导学生在理解的基础上,得出平方差公式的使用条件。(10分钟) 在ppt上展示以下题目, 下列各题哪些可以使用平方差公式: (1) (-a+b)(a+b) (2) (a-b)(b+a) (3) (a+b)(-a-b) (4) (-b-a)(b-a) (5) (-b+a)(-a-b) 教师组织学生梳理和总结得出,平方差公式的使用条件:两个多项式中有一项完全相同,另一项互为相反数(一同一反)对于变形的平方差公式,当符号或位置变化,运用同前异后法。 例题讲解,加深学生理解(10分钟) 例1、 (1) (-x-y) (y-x) (2) (3+a) (-3+a) 抽学生上台做题,共同判断正误,并进行点评,给予适当表扬。 紧接着提出平方差公式在符号或位置不同以外,还可能存在系数或指数不同的情况,给出以下例题,总结出人坚不拆法。 例2、 (1) (3x+2) (3x-2) (2) (3a +b3) (3a -b3) 学生就教师的提问进行思考并在教师的引导下得出平方差公式的文字叙述。 教师引导学生通过自主探究,认识到:使用条件是两个多项式中有一项完全相同,另一项互为相反数。(一同一反)并总结出同前异后法。 例1抽学生上讲台做,其余同学自行思考,教师进行讲解并规范书写。 例2教师与学生共同解决问题,并总结出人坚不拆法。 通过设置问题,层层提问,引导学生进行思考并进一步讨论。学生采用小组讨论和自主探究等多种学习方法,进行问题的探究,提高了学生的合作交流、语言表达能力。 首先是通过5个式子,观察得出使用条件,进而得出招式一同前异后。 例1的设计是为了及时巩固学生对同前异后法的理解,了解学生的掌握情况。 例2的设计是针对于系数或指数发生变化的情况,指出了易错点,引出人坚不拆法。
( 4分钟) 课堂练习 1.下列各式能用平方差公式计算的是( ). A. (3a+b)(a-b) B. (-3a-b)(-3a+b) C. (3a+b)(-3a-b) D. (-3a+b)(3a-b) 2.(-4a-1)与(4a-1)的积等于( ). A. -1+16a2 B. -1-8a2 C. 1-4a2 D. 1-16a2 学生们自主思考,得出答案。教师抽学生回答,针对学生出现的问题给予适当的说明。 通过设置适当的练习题,可以加深学生对平方差公式使用条件和变形情况使用方法的理解,巩固知识。
(2分钟) 课堂小结 教师引导学生从知识、能力或情感等方面畅谈本节课的收获,针对学生的回答,采用多种方式进行评价并总结。通过本节课的学习,我们学到了以下知识: 平方差公式(a+b)(a-b)=a -b 两数和与这两数的差的积,等于它们的平方差 2、使用条件:两个多项式中有一项完全相同,另一项互为相反数 3、变形情况: 符号或位置变化——同前异后 系数或指数变化——人坚不拆法 学生们畅所欲言,分享本节课的收获。教师加以总结,进一步加深学生对公式的理解。 通过小结,让学生进一步巩固本节所学内容,并能够灵活运用。
作业布置 课本P112 习题14.2 第1题(必做) 第5题(选做) 通过分层设置课后作业,考虑到学生的不同基础,使学生更好的掌握知识。
板书设计
§14.2.1平方差公式 1.平方差公式 (a+b)(a-b)=a -b 和 差 平方差 2.使用条件:一同一反 3.变形: (1)同前异后 (2)人坚不拆法 PPT 演算板书
教学反思
本节课采用情景-探究的方式,以猜想、实验、论证为主要探究方式,得出平方差公式,应用逆向思维的方向,演绎出平方差公式,对公式的应用首先提醒学生要注意其特征,其次要做好式子的变形,把问题转化成能够应用公式的方面上来,应用公式法因式分解的过程,实际上就是转化和化归的过程。在解决认识平方差公式的结构时候,重点突出学生自我思想的形成,能够充分地不公式用自己的语言来叙述,在整个教学设计中,教师只作为了一个点拨者和引路人。然后应用有梯度的典型例题加以巩固,在学生头脑中形成一个清晰完整的数学模型,使学生在今后的练习中游刃有余。
不足之处:
教学中时间把握还是不足,在设计的题目中不怎么合理,应按题目的难度从易到难。
有些题目的归纳可放手给学生讨论后由学生说出,而不是教师代替。小组评价做的不够,没有足够的小组的活动,没有小组的竞赛。教学语言还太随意,数学的语言应该严谨。在语调上应该有所变化。
