24.2点和圆、直线和圆的位置关系 同步练习 2023-2024学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 24.2点和圆、直线和圆的位置关系 同步练习 2023-2024学年人教版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 00:00:00 | ||
图片预览



文档简介
24.2点和圆、直线和圆的位置关系 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
3.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA = 30°,则OB的长为( )
A. B.4 C. D.2
4.如图,,是的切线,点,是切点,点是上一点,连结和.若,则的度数为( )
A.50° B.65° C.75° D.130°
5.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
6.已知,如图,点C是以AB为直径的半圆O上一点,过点C作⊙O的切线CD,BD⊥CD于点D,若∠DCB=50°,则∠ABC的度数是( )
A.25° B.40° C.45° D.50°
7.如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4cm B.3cm C.2cm D.1.5cm
8.如图,AB、AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD,若∠DAC=78°,则∠ADO等于( )
A.70° B.64° C.62° D.51°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若三角形的三边长分别为6、8、10,则此三角形的内切圆半径为 .
10.在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为
11.如图,是的直径,是的切线,A为切点,连接,与交于点D,连接,若,则 .
12.如图,AB为⊙O的直径,C为⊙O外一点,过C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=42°.点E在AB右侧的半圆周上运动(不与A,B重合),则∠AED的度数为 .
13.如图,直线y= +3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为 cm2.
三、解答题:(本题共5题,共45分)
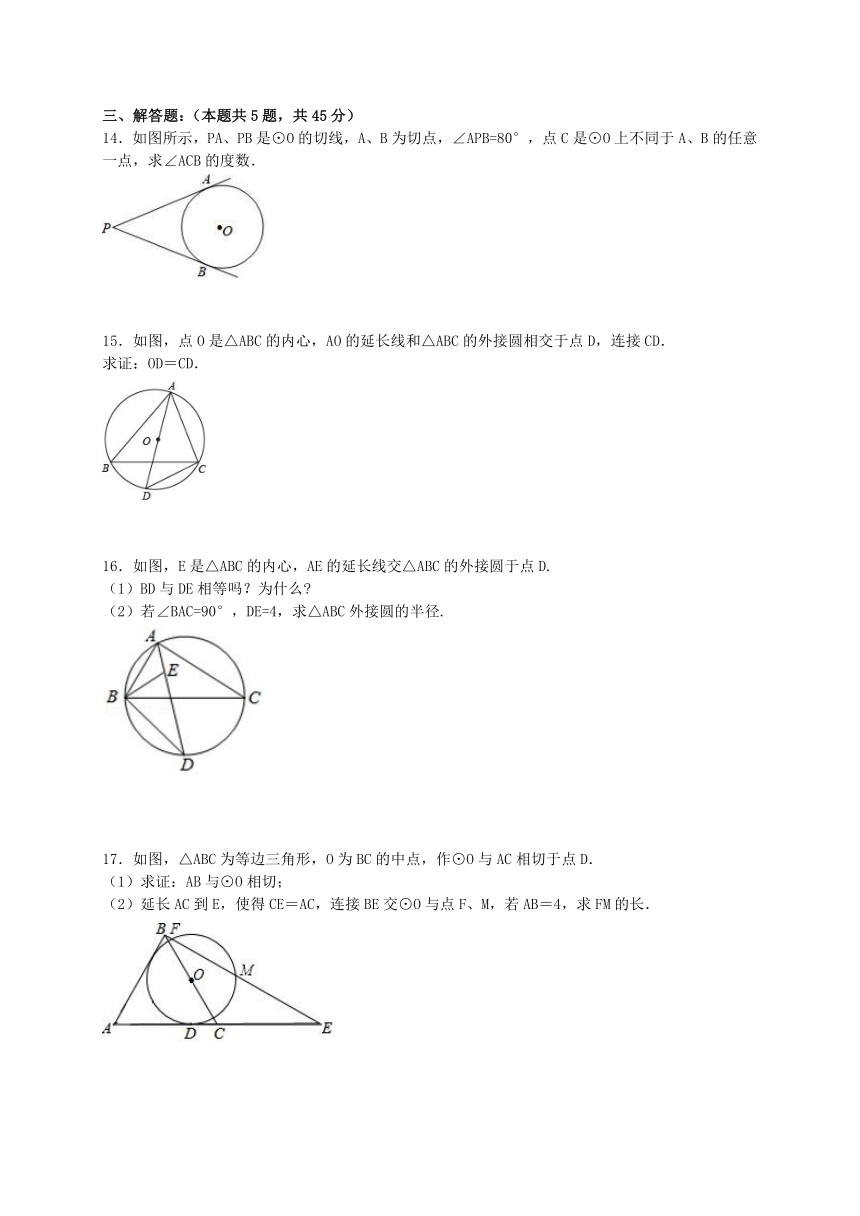
14.如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.
15.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连接CD.
求证:OD=CD.
16.如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D.
(1)BD与DE相等吗?为什么
(2)若∠BAC=90°,DE=4,求△ABC外接圆的半径.
17.如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
18.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC.
(2)若PC=2 ,求⊙O的半径.
参考答案:
1.A 2.B 3.B 4.B 5.B 6.B 7.B 8.B
9.2
10.12<r<13
11.49°
12.42°
13.11
14.解:连接OA、OB,在AB弧上任取一点C,连接AC、BC.
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°.
∵∠APB=80°,在四边形OAPB中,可得∠AOB=100°.
分两种情况讨论:
①若C点在劣弧AB上,则∠ACB=130°;
②若C点在优弧AB上,则∠ACB=50°.
15.证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
16.(1)解: DE=DB。
∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴ = ,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)解: 连接CD,如图所示:
由(1)得: = ,
∴CD=BD=DE=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC= =4 ,
∴△ABC外接圆的半径:r=2
17.(1)证明:连接OD,作OG⊥AB于G,如图1所示:
则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中, ,
∴△OBG≌△OCD(AAS),
∴OG=OD,∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:
则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB= ∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB= BC= AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG= OB=1,OG= BG= ,
在Rt△OMH中,OM=OG= ,OH=1,
∴MH= = ,
∴FM=2MH=2 .
18.(1)证明:连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC
(2)证明:设⊙O的半径为r,
在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,
AC2=(2 )2﹣(5﹣r)2,
∵AB=AC,
∴52﹣r2=(2 )2﹣(5﹣r)2,
解得:r=3,
则⊙O的半径为3
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
3.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA = 30°,则OB的长为( )
A. B.4 C. D.2
4.如图,,是的切线,点,是切点,点是上一点,连结和.若,则的度数为( )
A.50° B.65° C.75° D.130°
5.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有( )个:
①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.
A.1 B.2 C.3 D.4
6.已知,如图,点C是以AB为直径的半圆O上一点,过点C作⊙O的切线CD,BD⊥CD于点D,若∠DCB=50°,则∠ABC的度数是( )
A.25° B.40° C.45° D.50°
7.如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4cm B.3cm C.2cm D.1.5cm
8.如图,AB、AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD,若∠DAC=78°,则∠ADO等于( )
A.70° B.64° C.62° D.51°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若三角形的三边长分别为6、8、10,则此三角形的内切圆半径为 .
10.在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为
11.如图,是的直径,是的切线,A为切点,连接,与交于点D,连接,若,则 .
12.如图,AB为⊙O的直径,C为⊙O外一点,过C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=42°.点E在AB右侧的半圆周上运动(不与A,B重合),则∠AED的度数为 .
13.如图,直线y= +3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为 cm2.
三、解答题:(本题共5题,共45分)
14.如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.
15.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连接CD.
求证:OD=CD.
16.如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D.
(1)BD与DE相等吗?为什么
(2)若∠BAC=90°,DE=4,求△ABC外接圆的半径.
17.如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
18.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC.
(2)若PC=2 ,求⊙O的半径.
参考答案:
1.A 2.B 3.B 4.B 5.B 6.B 7.B 8.B
9.2
10.12<r<13
11.49°
12.42°
13.11
14.解:连接OA、OB,在AB弧上任取一点C,连接AC、BC.
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°.
∵∠APB=80°,在四边形OAPB中,可得∠AOB=100°.
分两种情况讨论:
①若C点在劣弧AB上,则∠ACB=130°;
②若C点在优弧AB上,则∠ACB=50°.
15.证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
16.(1)解: DE=DB。
∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴ = ,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)解: 连接CD,如图所示:
由(1)得: = ,
∴CD=BD=DE=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC= =4 ,
∴△ABC外接圆的半径:r=2
17.(1)证明:连接OD,作OG⊥AB于G,如图1所示:
则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中, ,
∴△OBG≌△OCD(AAS),
∴OG=OD,∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:
则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB= ∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB= BC= AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG= OB=1,OG= BG= ,
在Rt△OMH中,OM=OG= ,OH=1,
∴MH= = ,
∴FM=2MH=2 .
18.(1)证明:连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC
(2)证明:设⊙O的半径为r,
在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,
AC2=(2 )2﹣(5﹣r)2,
∵AB=AC,
∴52﹣r2=(2 )2﹣(5﹣r)2,
解得:r=3,
则⊙O的半径为3
同课章节目录
