23.1图形的旋转 同步练习 2023-2024学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 23.1图形的旋转 同步练习 2023-2024学年人教版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 20:59:52 | ||
图片预览


文档简介
23.1图形的旋转 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.一个平行四边形绕着对角线的交点旋转90°能够与本身重合,则该平行四边形为( )
A.矩形 B.菱形 C.正方形 D.无法确定
2.在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A.(﹣4,3) B.(﹣3,4) C.(3,﹣4) D.(4,﹣3)
3.如图,将△AOB绕点O按逆时针方向旋转50°后得到△COD,若∠AOB=15°,则∠BOC的度数是( )
A.35° B.45° C.55° D.65°
4.如图,在中,,,将绕点C按顺时针方向旋转后得到,此时点D在AB边上,则旋转角的大小为( )
A.20° B.40° C.70° D.50°
5.如图,在△ABC中,AB=2.2,BC=3.6,∠B=60°,将△ABC绕点A按逆时针方向旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为( )
A.1.5 B.1.4 C.1.3 D.1.2
6.如图,等腰直角三角形中,,,将绕点B顺时针旋转,得到,连接,过点A作交的延长线于点H,连接,则的度数( )
A.随着 的增大而增大 B.随着 的增大而减小
C.保持定值不变 D.随着 的增大,先增大后减小
7.如图,在平面直角坐标系xOy中,直线 经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
A.(- ,2) B.(- ,1)
C.(-2, ) D.(-1, )
8.如图,将矩形绕点A逆时针旋转至矩形的位置,点B的对应点是点,点C的对应点是点,点在的延长线上,交于点E.若,则的长为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是 .
10.如图,点P是等边三角形ABC内的一点,若将△PAB绕点A逆时针旋转到△P′AC,则∠PAP′的度数为 .
11.如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,当C1D1第一次经过顶点C时,旋转角∠ABA1= .
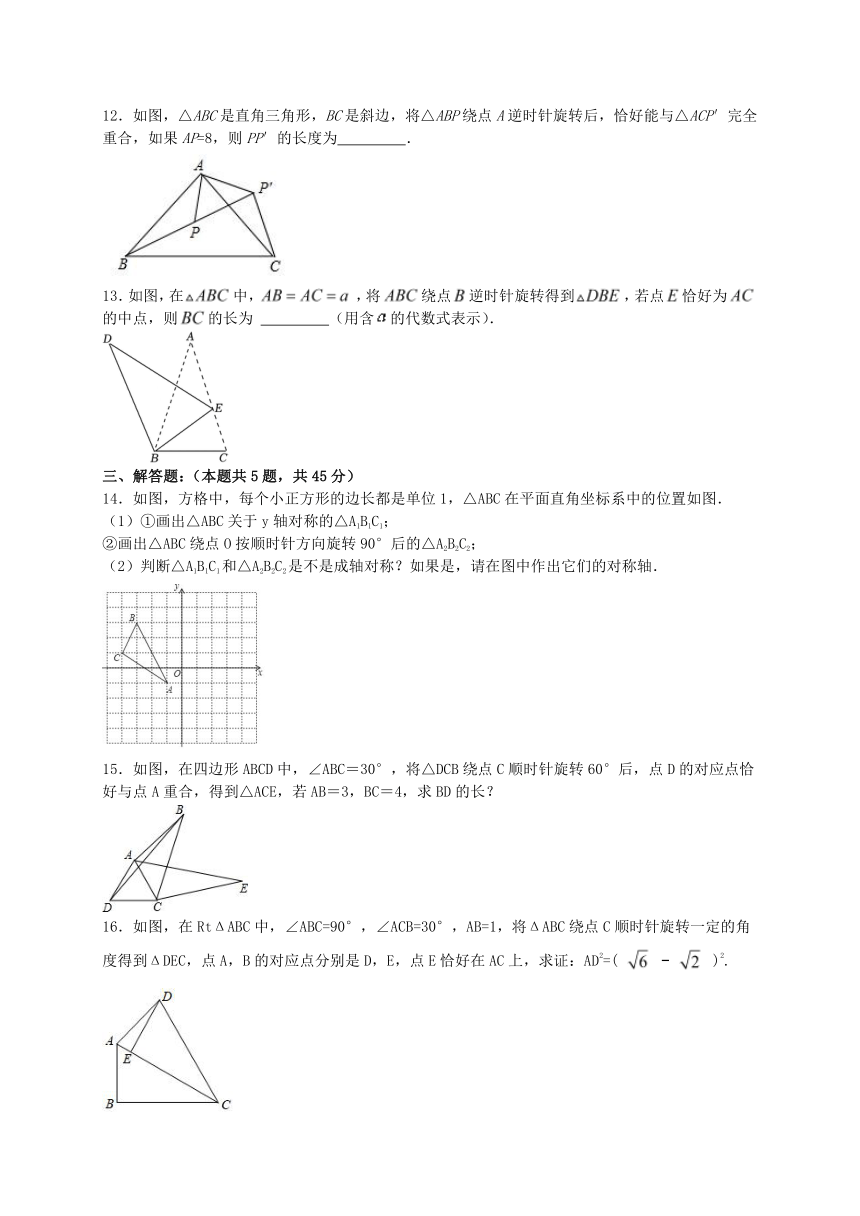
12.如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,恰好能与△ACP′完全重合,如果AP=8,则PP′的长度为 .
13.如图,在中,,将绕点逆时针旋转得到,若点恰好为的中点,则的长为 (用含的代数式表示).
三、解答题:(本题共5题,共45分)
14.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC绕点O按顺时针方向旋转90°后的△A2B2C2;
(2)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,求BD的长?
16.如图,在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,将ΔABC绕点C顺时针旋转一定的角度得到ΔDEC,点A,B的对应点分别是D,E,点E恰好在AC上,求证:AD2=( )2.
17.如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
18.如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
参考答案:
1.C 2.A 3.A 4.B 5.B 6.C 7.D 8.B
9.90°
10.60°
11.30°
12.
13.
14.(1)解:①如图,△A1B1C1即为所求作三角形;
②如图,△A2B2C2即为所求作三角形;
(2)如图,直线l即为△A1B1C1和△A2B2C2的对称轴
15.解:连接BE,如图,
∵△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,
∴∠BCE=60°,CB=CE,BD=AE,
∴△BCE为等边三角形,
∴BE=BC=4,∠CBE=60°,
∵∠ABC=30°,
∴∠ABE=90°,
在Rt△ABE中,AE= =5,
∴BD=5.
16.解:在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,
∴AC=2AB=2,BC= AB= ,
根据旋转的性质得:DE=AB=1,CE=BC= ,∠DEC=∠ABC=90°,
∴AE=AC-CE=2- ,∠AED=90°,
在RtΔADE中, ,
∴ .
17.(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,
18.(1)解:旋转的中心是点A,旋转的角度是90°;
(2)解:△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)解:∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)解:AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.一个平行四边形绕着对角线的交点旋转90°能够与本身重合,则该平行四边形为( )
A.矩形 B.菱形 C.正方形 D.无法确定
2.在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A.(﹣4,3) B.(﹣3,4) C.(3,﹣4) D.(4,﹣3)
3.如图,将△AOB绕点O按逆时针方向旋转50°后得到△COD,若∠AOB=15°,则∠BOC的度数是( )
A.35° B.45° C.55° D.65°
4.如图,在中,,,将绕点C按顺时针方向旋转后得到,此时点D在AB边上,则旋转角的大小为( )
A.20° B.40° C.70° D.50°
5.如图,在△ABC中,AB=2.2,BC=3.6,∠B=60°,将△ABC绕点A按逆时针方向旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为( )
A.1.5 B.1.4 C.1.3 D.1.2
6.如图,等腰直角三角形中,,,将绕点B顺时针旋转,得到,连接,过点A作交的延长线于点H,连接,则的度数( )
A.随着 的增大而增大 B.随着 的增大而减小
C.保持定值不变 D.随着 的增大,先增大后减小
7.如图,在平面直角坐标系xOy中,直线 经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
A.(- ,2) B.(- ,1)
C.(-2, ) D.(-1, )
8.如图,将矩形绕点A逆时针旋转至矩形的位置,点B的对应点是点,点C的对应点是点,点在的延长线上,交于点E.若,则的长为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是 .
10.如图,点P是等边三角形ABC内的一点,若将△PAB绕点A逆时针旋转到△P′AC,则∠PAP′的度数为 .
11.如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1,当C1D1第一次经过顶点C时,旋转角∠ABA1= .
12.如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,恰好能与△ACP′完全重合,如果AP=8,则PP′的长度为 .
13.如图,在中,,将绕点逆时针旋转得到,若点恰好为的中点,则的长为 (用含的代数式表示).
三、解答题:(本题共5题,共45分)
14.如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC绕点O按顺时针方向旋转90°后的△A2B2C2;
(2)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
15.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,求BD的长?
16.如图,在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,将ΔABC绕点C顺时针旋转一定的角度得到ΔDEC,点A,B的对应点分别是D,E,点E恰好在AC上,求证:AD2=( )2.
17.如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
18.如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
参考答案:
1.C 2.A 3.A 4.B 5.B 6.C 7.D 8.B
9.90°
10.60°
11.30°
12.
13.
14.(1)解:①如图,△A1B1C1即为所求作三角形;
②如图,△A2B2C2即为所求作三角形;
(2)如图,直线l即为△A1B1C1和△A2B2C2的对称轴
15.解:连接BE,如图,
∵△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,
∴∠BCE=60°,CB=CE,BD=AE,
∴△BCE为等边三角形,
∴BE=BC=4,∠CBE=60°,
∵∠ABC=30°,
∴∠ABE=90°,
在Rt△ABE中,AE= =5,
∴BD=5.
16.解:在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,
∴AC=2AB=2,BC= AB= ,
根据旋转的性质得:DE=AB=1,CE=BC= ,∠DEC=∠ABC=90°,
∴AE=AC-CE=2- ,∠AED=90°,
在RtΔADE中, ,
∴ .
17.(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,
18.(1)解:旋转的中心是点A,旋转的角度是90°;
(2)解:△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)解:∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)解:AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
同课章节目录
