23.2中心对称 同步练习 2023-2024学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 23.2中心对称 同步练习 2023-2024学年人教版数学九年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 126.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 21:01:01 | ||
图片预览


文档简介
23.2中心对称 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
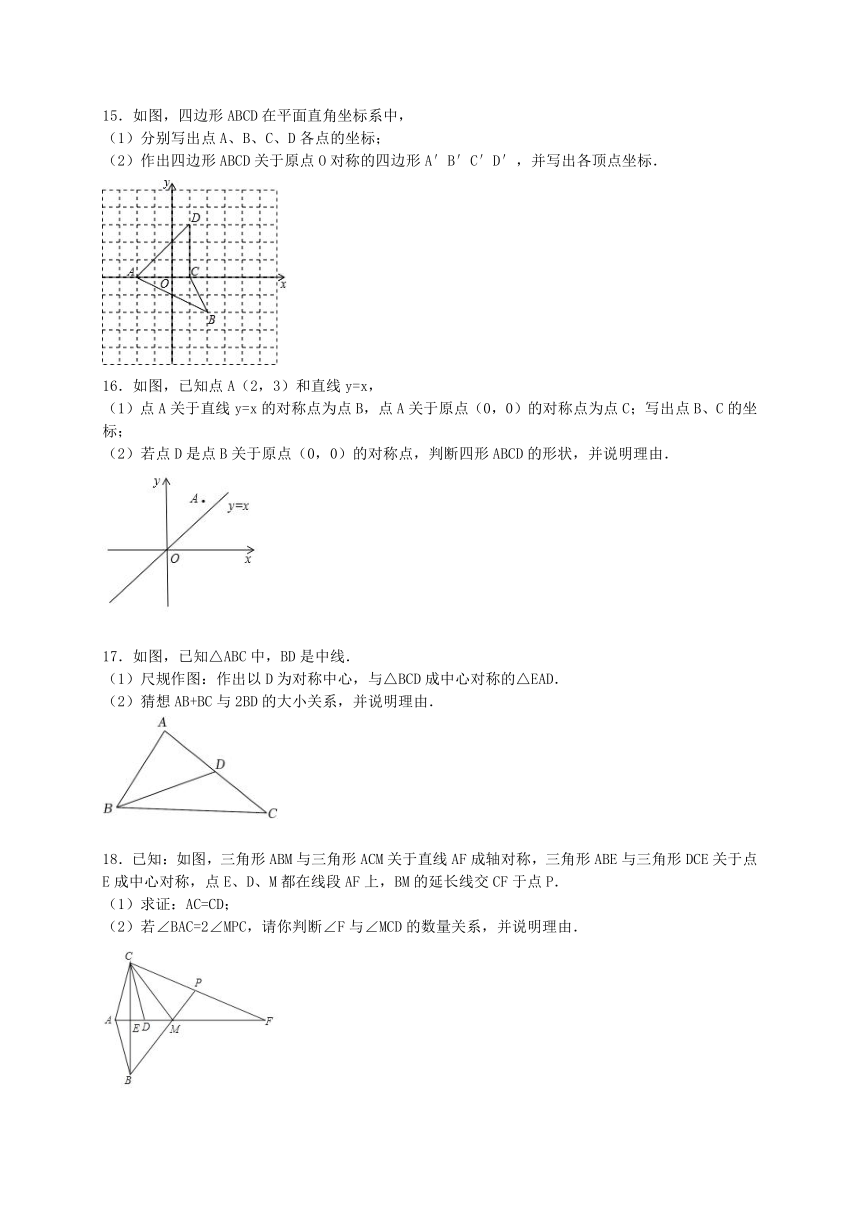
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列图形中是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
3.将一个等腰三角形沿底边上的中线剪开,用剪下的两个三角形拼成的所有四边形中,是中心对称图形的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,△ABC与△A′B′C′是中心对称的两个图形,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′
C.AB∥A′B′ D.S△ABO=S△A′B′C′
5.如图所示,在矩形中,,与相交于点O,下列说法正确的是( )
A.点O为矩形的对称中心
B.点O为线段的对称中心
C.直线为矩形的对称轴
D.直线为线段的对称轴
6.已知点P(a+1,﹣ +1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.如图,线段是由线段a经过平移得到的,线段还可以看作是线段a经过怎样的图形变化得到?下列结论:①1次中心对称;②1次轴对称;③2次轴对称.其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
8.△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )
A.(4,﹣2) B.(﹣4,﹣2)
C.(﹣2,﹣3) D.(﹣2,﹣4)
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若点与关于原点成中心对称,则 .
10.已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为 。
11.如果点A(﹣3,2m+1)关于原点对称的点在第一象限,则m的取值范围是 .
12.如图, 和 关于点C成中心对称,若 , , ,则 的长是 .
13.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为 ,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为 .
三、解答题:(本题共5题,共45分)
14.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段.
15.如图,四边形ABCD在平面直角坐标系中,
(1)分别写出点A、B、C、D各点的坐标;
(2)作出四边形ABCD关于原点O对称的四边形A′B′C′D′,并写出各顶点坐标.
16.如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.
17.如图,已知△ABC中,BD是中线.
(1)尺规作图:作出以D为对称中心,与△BCD成中心对称的△EAD.
(2)猜想AB+BC与2BD的大小关系,并说明理由.
18.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
参考答案:
1.C 2.A 3.C 4.D 5.A 6.C 7.C 8.B
9.
10.(1,3)
11.
12.
13.(-1,-3);(-3,-3)
14.作法如下:
图中A的对应点是D,B的对应点是E,C的对应点是F;AB对应线段是DE,BC对应线段是EF,CD对应线段是AF.
15.(1)解:A(0,﹣2),B(2,﹣2),C(1,0),D(1,3);
(2)解:如图所示:A′(0,2),B′(﹣2,2),C′(﹣1,0),D(﹣1,﹣3).
16.解:(1)∵A(2,3),
∴点A关于直线y=x的对称点B(3,2),
点A关于原点(0,0)的对称点C(﹣2,﹣3);
(2)∵B(3,2),
∴点B关于原点(0,0)的对称点D(﹣3,﹣2),
∵点B与点D关于O对称,
∴BO=DO,
∵点A与点C关于O对称,
∴AO=CO,
∴四边形ABCD是平行四边形,
∵点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C,
∴AC=BD,
∴平行四边形ABCD是矩形.
17.(1)解:延长BD,在BD延长线上截取DE=BD,连结AE,
则△ADE与△CDB关于点D成中心对称,
∵点D为AC中点,
∴AD=CD,
在△ADE和△CDB中,
,
∴△ADE≌△CDB(SAS),
∵∠CDB+∠ADB=180°,
∴△BCD绕点D旋转180°得到△EAD,
(2)解:AB+BC>2BD.
证明:∵△ADE≌△CDB(SAS),
∴AE=BC,BD=ED,
∴BE=2BD,
在△ABE中,AB+AE>BE,
即AB+BC>2BD.
18.(1)证明:∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM,
∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,
∴AB=CD,
∴AC=CD;
(2)解:∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列图形中是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
3.将一个等腰三角形沿底边上的中线剪开,用剪下的两个三角形拼成的所有四边形中,是中心对称图形的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,△ABC与△A′B′C′是中心对称的两个图形,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′
C.AB∥A′B′ D.S△ABO=S△A′B′C′
5.如图所示,在矩形中,,与相交于点O,下列说法正确的是( )
A.点O为矩形的对称中心
B.点O为线段的对称中心
C.直线为矩形的对称轴
D.直线为线段的对称轴
6.已知点P(a+1,﹣ +1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.如图,线段是由线段a经过平移得到的,线段还可以看作是线段a经过怎样的图形变化得到?下列结论:①1次中心对称;②1次轴对称;③2次轴对称.其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
8.△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )
A.(4,﹣2) B.(﹣4,﹣2)
C.(﹣2,﹣3) D.(﹣2,﹣4)
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若点与关于原点成中心对称,则 .
10.已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为 。
11.如果点A(﹣3,2m+1)关于原点对称的点在第一象限,则m的取值范围是 .
12.如图, 和 关于点C成中心对称,若 , , ,则 的长是 .
13.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为 ,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为 .
三、解答题:(本题共5题,共45分)
14.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段.
15.如图,四边形ABCD在平面直角坐标系中,
(1)分别写出点A、B、C、D各点的坐标;
(2)作出四边形ABCD关于原点O对称的四边形A′B′C′D′,并写出各顶点坐标.
16.如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.
17.如图,已知△ABC中,BD是中线.
(1)尺规作图:作出以D为对称中心,与△BCD成中心对称的△EAD.
(2)猜想AB+BC与2BD的大小关系,并说明理由.
18.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
参考答案:
1.C 2.A 3.C 4.D 5.A 6.C 7.C 8.B
9.
10.(1,3)
11.
12.
13.(-1,-3);(-3,-3)
14.作法如下:
图中A的对应点是D,B的对应点是E,C的对应点是F;AB对应线段是DE,BC对应线段是EF,CD对应线段是AF.
15.(1)解:A(0,﹣2),B(2,﹣2),C(1,0),D(1,3);
(2)解:如图所示:A′(0,2),B′(﹣2,2),C′(﹣1,0),D(﹣1,﹣3).
16.解:(1)∵A(2,3),
∴点A关于直线y=x的对称点B(3,2),
点A关于原点(0,0)的对称点C(﹣2,﹣3);
(2)∵B(3,2),
∴点B关于原点(0,0)的对称点D(﹣3,﹣2),
∵点B与点D关于O对称,
∴BO=DO,
∵点A与点C关于O对称,
∴AO=CO,
∴四边形ABCD是平行四边形,
∵点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C,
∴AC=BD,
∴平行四边形ABCD是矩形.
17.(1)解:延长BD,在BD延长线上截取DE=BD,连结AE,
则△ADE与△CDB关于点D成中心对称,
∵点D为AC中点,
∴AD=CD,
在△ADE和△CDB中,
,
∴△ADE≌△CDB(SAS),
∵∠CDB+∠ADB=180°,
∴△BCD绕点D旋转180°得到△EAD,
(2)解:AB+BC>2BD.
证明:∵△ADE≌△CDB(SAS),
∴AE=BC,BD=ED,
∴BE=2BD,
在△ABE中,AB+AE>BE,
即AB+BC>2BD.
18.(1)证明:∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM,
∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,
∴AB=CD,
∴AC=CD;
(2)解:∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD
同课章节目录
