12.1全等三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.1全等三角形 同步练习 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 123.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 21:01:33 | ||
图片预览

文档简介
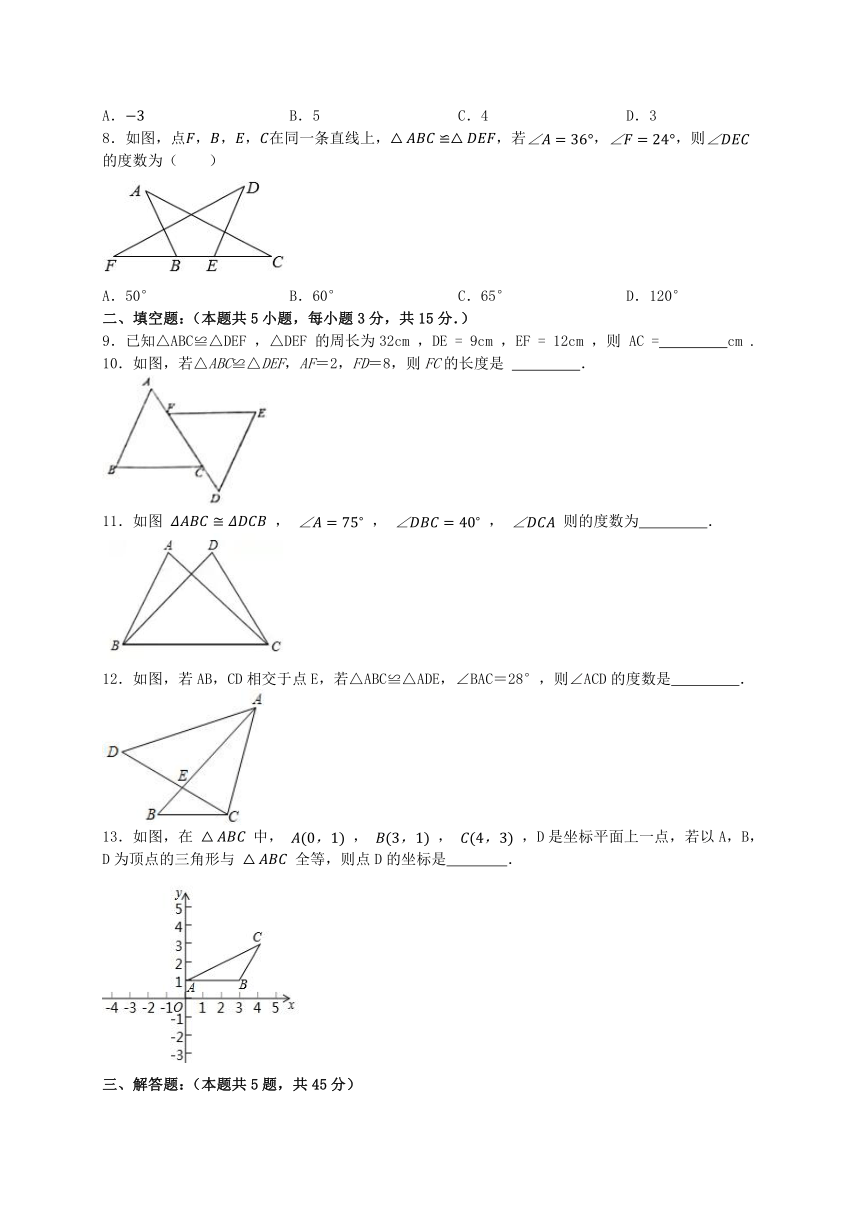
12.1全等三角形 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列命题中,为假命题的是( )
A.全等三角形的对应边相等 B.全等三角形的对应角相等
C.全等三角形的面积相等 D.面积相等的两个三角形全等
2.下列四个图形中,属于全等图形的是( )
A.①和② B.②和③ C.①和③ D.②和④
3.已知△ABC≌△DEF,点A与D,点C与F分别是对应点,则∠B的对应角是( )
A.∠A B.∠F C.∠E D.∠C
4.如图,△ABC≌△A'B'C',则∠C的度数是( )
A.107° B.73° C.56° D.51°
5.如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中△ABC是格点三角形,请你找出方格中所有与△ABC全等,且以A为顶点的格点三角形,这样的三角形共有( )个(△ABC除外).
A.2 B.3 C.4 D.5
6.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
7.如图, ,且点A、B的坐标分别为 ,则 长是( )
A. B.5 C.4 D.3
8.如图,点,,,在同一条直线上,,若,,则的度数为( )
A.50° B.60° C.65° D.120°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知△ABC≌△DEF ,△DEF 的周长为32cm ,DE = 9cm ,EF = 12cm ,则 AC = cm .
10.如图,若△ABC≌△DEF,AF=2,FD=8,则FC的长度是 .
11.如图 , , , 则的度数为 .
12.如图,若AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠ACD的度数是 .
13.如图,在 中, , , ,D是坐标平面上一点,若以A,B,D为顶点的三角形与 全等,则点D的坐标是 .
三、解答题:(本题共5题,共45分)
14.如图, , , ,求 的度数.
15.如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105 ,∠B=50 ,∠CAD=10°,求出∠DEF的度数.
16.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
17.如图所示, , , 三点在同一直线上,且 .
(1)求证: ;
(2)当 满足什么条件时, ?
18.如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
参考答案:
1.D 2.D 3.C 4.B 5.D 6.B 7.D 8.B
9.11
10.6
11.25°
12.76°
13.D1(-1,3),D2(4,-1),D3(-1,-1)
14.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°-∠A-∠ACB=96°.
15.解:∵∠ACB=105°,∠B=50°,
∴∠CAB=180° ∠B ∠ACB=180° 50° 105°=25°.
又∵△ABC≌△ADE,
∴∠D=∠B=50°.
又∵∠ACF=180° 105°=75°,∠CAD=10°,
∴∠AFC=180° 75° 10°=95°,
∴∠EFD=95°,
∴∠DEF=180° 95° 50°=35°.
16.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC= (∠EAB﹣∠CAD)= .
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
17.(1)证明:∵ ,
∴AE=BC,AC=DE,
又∵ ,
∴ .
(2)解:若 ,则 ,
又∵ ,
∴ ,
∴ ,
又∵ ,
∴ ,
即当 满足 为直角时, .
18.(1)证明:∵≌,
∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,
∴;
(2)解:∵,,
∴∠CAE=35°,
∵≌,
∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,
∴∠BED=∠CAE=35°
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列命题中,为假命题的是( )
A.全等三角形的对应边相等 B.全等三角形的对应角相等
C.全等三角形的面积相等 D.面积相等的两个三角形全等
2.下列四个图形中,属于全等图形的是( )
A.①和② B.②和③ C.①和③ D.②和④
3.已知△ABC≌△DEF,点A与D,点C与F分别是对应点,则∠B的对应角是( )
A.∠A B.∠F C.∠E D.∠C
4.如图,△ABC≌△A'B'C',则∠C的度数是( )
A.107° B.73° C.56° D.51°
5.如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中△ABC是格点三角形,请你找出方格中所有与△ABC全等,且以A为顶点的格点三角形,这样的三角形共有( )个(△ABC除外).
A.2 B.3 C.4 D.5
6.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
7.如图, ,且点A、B的坐标分别为 ,则 长是( )
A. B.5 C.4 D.3
8.如图,点,,,在同一条直线上,,若,,则的度数为( )
A.50° B.60° C.65° D.120°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知△ABC≌△DEF ,△DEF 的周长为32cm ,DE = 9cm ,EF = 12cm ,则 AC = cm .
10.如图,若△ABC≌△DEF,AF=2,FD=8,则FC的长度是 .
11.如图 , , , 则的度数为 .
12.如图,若AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠ACD的度数是 .
13.如图,在 中, , , ,D是坐标平面上一点,若以A,B,D为顶点的三角形与 全等,则点D的坐标是 .
三、解答题:(本题共5题,共45分)
14.如图, , , ,求 的度数.
15.如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105 ,∠B=50 ,∠CAD=10°,求出∠DEF的度数.
16.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
17.如图所示, , , 三点在同一直线上,且 .
(1)求证: ;
(2)当 满足什么条件时, ?
18.如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
参考答案:
1.D 2.D 3.C 4.B 5.D 6.B 7.D 8.B
9.11
10.6
11.25°
12.76°
13.D1(-1,3),D2(4,-1),D3(-1,-1)
14.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°-∠A-∠ACB=96°.
15.解:∵∠ACB=105°,∠B=50°,
∴∠CAB=180° ∠B ∠ACB=180° 50° 105°=25°.
又∵△ABC≌△ADE,
∴∠D=∠B=50°.
又∵∠ACF=180° 105°=75°,∠CAD=10°,
∴∠AFC=180° 75° 10°=95°,
∴∠EFD=95°,
∴∠DEF=180° 95° 50°=35°.
16.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC= (∠EAB﹣∠CAD)= .
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
17.(1)证明:∵ ,
∴AE=BC,AC=DE,
又∵ ,
∴ .
(2)解:若 ,则 ,
又∵ ,
∴ ,
∴ ,
又∵ ,
∴ ,
即当 满足 为直角时, .
18.(1)证明:∵≌,
∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,
∴;
(2)解:∵,,
∴∠CAE=35°,
∵≌,
∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,
∴∠BED=∠CAE=35°
