12.2三角形全等的判定 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.2三角形全等的判定 同步练习 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 21:02:17 | ||
图片预览


文档简介
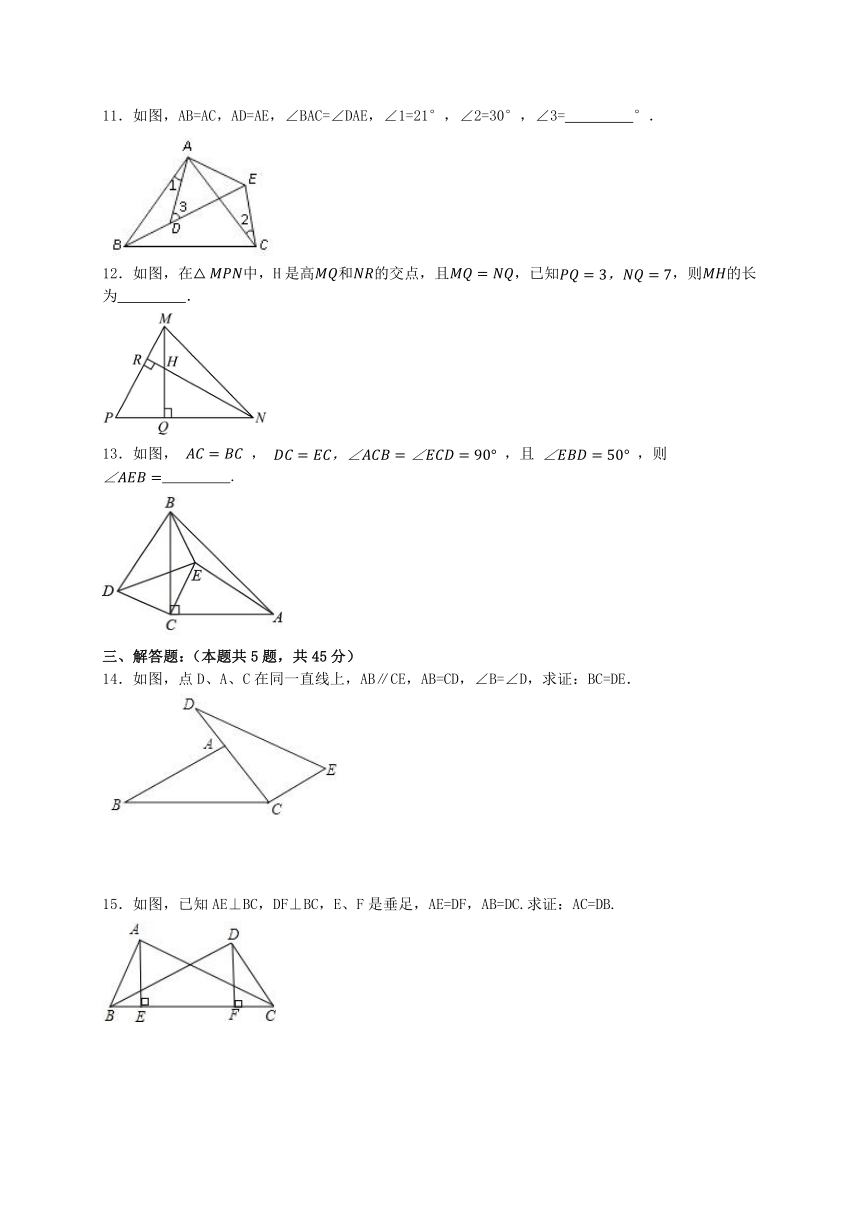
12.2三角形全等的判定 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.使两个直角三角形全等的条件是
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条边对应相等
2.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是
A. B. C. D.
3.下图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断 与下列哪一个三角形全等?( )
A.△ACF B.△AED C.△ABC D.△BCF
4.如图,CD丄AB于D,BE丄AC于E,BE与CD交于O,OB=OC ,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
5.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
A.全部正确 B.仅①和②正确
C.仅①正确 D.仅①和③正确
6.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=13,则CF=( )
A.10 B.8 C.7 D.6
7.如图,已知是的平分线,,若,则的面积( )
A. B. C. D.不能确定
8.如图,中,分别是其角平分线和中线,过点C作于F,连接,则线段的长为( )
A. B.2 C. D.3
二、填空题:(本题共5小题,每小题3分,共15分.)
9.如图,和中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使得和全等,(写出一个即可)
10.如图,要测量小金河两岸相对的A、两点之间的距离,可以在与垂直的河岸上取、两点,且使.从点出发沿与河岸垂直的方向移动到点,使点A、、在一条直线上.若测量的长为28米,则A、两点之间的距离为 米.
11.如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=30°,∠3= °.
12.如图,在中,H是高和的交点,且,已知,则的长为 .
13.如图, , ,且 ,则 .
三、解答题:(本题共5题,共45分)
14.如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
15.如图,已知AE⊥BC,DF⊥BC,E、F是垂足,AE=DF,AB=DC.求证:AC=DB.
16.如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.
(1)求证:DE=EF;
(2)当∠A=36°时,求∠DEF的度数.
17.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.
(1)请你找出图中其他的全等三角形;
(2)试证明CF=EF.
18.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BD=AD,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)求证:BE=AC;
(2)试判断线段AC与线段MC的关系,并证明你的结论.
参考答案:
1.D 2.B 3.B 4.C 5.B 6.C 7.A 8.B
9.(答案不唯一)
10.28
11.51°
12.4
13.140°
14.证明:∵AB∥EC,
∴∠BAC=∠DCE,
在△ABC和△CDE中,
,
∴△ABC≌△CDE,
∴BC=DE.
15.证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=∠DFC=90°,
在Rt△ABE和Rt△DCF中, ,
∴Rt△ABE≌Rt△DCF(HL),
∴BE=CF,
∴BF=CE,
在△AEC和△DFB中, ,
∴△AEC≌△DFB(SAS),
∴AC=DB.
16.(1)证明:∵AD+EC=AB,AD+BD=AB,
∴BD=EC,
在△BDE和△CEF中 ,
∴△BDE≌△CEF(SAS),
∴DE=EF;
(2)解:∵△ABC中,∠A=36°,
∴∠B=∠C= (180°-36°)=72°,
由(1)知:△BDE≌△CEF,
∴∠BDE=∠CEF,
又∵∠DEF+∠CEF=∠B+∠BDE,
∴∠DEF=∠B=72°.
17.(1)解:图中其它的全等三角形为:①△ACD≌△AEB,②△DCF≌△BEF;
①∵Rt△ABC≌Rt△ADE,
∴AC=AE,AB=AD,∠BAC=∠DAE,
∵∠BAC﹣∠BAD=∠DAE﹣∠BAD,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
∵AC=AE,AD=AB,∠DAC=∠BAE,
∴△ADC≌△ABE(SAS);
②∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS).
(2)证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB(SAS),
∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS)
∴CF=EF.
18.(1)证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在△BDE与△ADC中,
,
∴△BDE≌△ADC(SAS),
∴BE=AC;
(2)解:AC⊥MC且AC=MC,理由如下:
∵F为BC中点,
∴BF=CF,
在△BFE与△CFM中,
,
∴△BFE≌△CFM(SAS),
∴∠CBE=∠BCM,BE=MC,
由(1)得:∠CBE=∠CAD,BE=AC,
∴∠CAD=∠BCM,AC=MC,
∵∠CAD+∠ACD=90°,
∴∠BCM+∠ACD=90°,
即∠ACM=90°,
∴AC⊥MC,
∴AC⊥MC且AC=MC
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.使两个直角三角形全等的条件是
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条边对应相等
2.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是
A. B. C. D.
3.下图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断 与下列哪一个三角形全等?( )
A.△ACF B.△AED C.△ABC D.△BCF
4.如图,CD丄AB于D,BE丄AC于E,BE与CD交于O,OB=OC ,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
5.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
A.全部正确 B.仅①和②正确
C.仅①正确 D.仅①和③正确
6.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=13,则CF=( )
A.10 B.8 C.7 D.6
7.如图,已知是的平分线,,若,则的面积( )
A. B. C. D.不能确定
8.如图,中,分别是其角平分线和中线,过点C作于F,连接,则线段的长为( )
A. B.2 C. D.3
二、填空题:(本题共5小题,每小题3分,共15分.)
9.如图,和中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使得和全等,(写出一个即可)
10.如图,要测量小金河两岸相对的A、两点之间的距离,可以在与垂直的河岸上取、两点,且使.从点出发沿与河岸垂直的方向移动到点,使点A、、在一条直线上.若测量的长为28米,则A、两点之间的距离为 米.
11.如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=30°,∠3= °.
12.如图,在中,H是高和的交点,且,已知,则的长为 .
13.如图, , ,且 ,则 .
三、解答题:(本题共5题,共45分)
14.如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
15.如图,已知AE⊥BC,DF⊥BC,E、F是垂足,AE=DF,AB=DC.求证:AC=DB.
16.如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.
(1)求证:DE=EF;
(2)当∠A=36°时,求∠DEF的度数.
17.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.
(1)请你找出图中其他的全等三角形;
(2)试证明CF=EF.
18.如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BD=AD,点F为BC的中点,连接EF并延长至点M,使FM=EF,连接CM.
(1)求证:BE=AC;
(2)试判断线段AC与线段MC的关系,并证明你的结论.
参考答案:
1.D 2.B 3.B 4.C 5.B 6.C 7.A 8.B
9.(答案不唯一)
10.28
11.51°
12.4
13.140°
14.证明:∵AB∥EC,
∴∠BAC=∠DCE,
在△ABC和△CDE中,
,
∴△ABC≌△CDE,
∴BC=DE.
15.证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=∠DFC=90°,
在Rt△ABE和Rt△DCF中, ,
∴Rt△ABE≌Rt△DCF(HL),
∴BE=CF,
∴BF=CE,
在△AEC和△DFB中, ,
∴△AEC≌△DFB(SAS),
∴AC=DB.
16.(1)证明:∵AD+EC=AB,AD+BD=AB,
∴BD=EC,
在△BDE和△CEF中 ,
∴△BDE≌△CEF(SAS),
∴DE=EF;
(2)解:∵△ABC中,∠A=36°,
∴∠B=∠C= (180°-36°)=72°,
由(1)知:△BDE≌△CEF,
∴∠BDE=∠CEF,
又∵∠DEF+∠CEF=∠B+∠BDE,
∴∠DEF=∠B=72°.
17.(1)解:图中其它的全等三角形为:①△ACD≌△AEB,②△DCF≌△BEF;
①∵Rt△ABC≌Rt△ADE,
∴AC=AE,AB=AD,∠BAC=∠DAE,
∵∠BAC﹣∠BAD=∠DAE﹣∠BAD,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
∵AC=AE,AD=AB,∠DAC=∠BAE,
∴△ADC≌△ABE(SAS);
②∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS).
(2)证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB(SAS),
∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS)
∴CF=EF.
18.(1)证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在△BDE与△ADC中,
,
∴△BDE≌△ADC(SAS),
∴BE=AC;
(2)解:AC⊥MC且AC=MC,理由如下:
∵F为BC中点,
∴BF=CF,
在△BFE与△CFM中,
,
∴△BFE≌△CFM(SAS),
∴∠CBE=∠BCM,BE=MC,
由(1)得:∠CBE=∠CAD,BE=AC,
∴∠CAD=∠BCM,AC=MC,
∵∠CAD+∠ACD=90°,
∴∠BCM+∠ACD=90°,
即∠ACM=90°,
∴AC⊥MC,
∴AC⊥MC且AC=MC
