13.2画轴对称图形 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 13.2画轴对称图形 同步练习 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 21:03:23 | ||
图片预览


文档简介
13.2画轴对称图形 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列剪纸作品中,是轴对称图形的为( )
A. B. C. D.
2.若点A(3,-4)与点B(-3,a)关于y轴对称,则a的值为( )
A.3 B.-3 C.4 D.-4
3.若一个点A的横坐标不变,纵坐标乘以﹣1后得到一个点B,则( )
A.点A与点B关于x轴对称 B.点A与点B关于y轴对称
C.点A与点B关于原点对称 D.点A向x轴的负方向平移1个单位得点B
4.已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )
A.﹣1 B.1 C.﹣3 D.3
5.如图,在直角坐标系中,各点坐标分别为,,.先作关于x轴成轴对称的,再把平移后得到.若,则点坐标为( )
A. B. C. D.
6.在平面直角坐标系中,已知点A关于直线x=1对称的点为B(-2,4),则点A的坐标为( )
A.(4,4) B.(-2,-2) C.(2,4) D.(3,4)
7.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( )
A.(-3,2) B.(2,3) C.(2,-3) D.(-2,-3)
8.如图,正方形OABC对角线交点为D,过D的直线分别交AB,OC于E,F,已知点E关于y轴的对称点坐标为(﹣ ,2),则图中阴影部分的面积是( )
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知点A(3,3)和点B是平面内两点,且它们关于直线x=2轴对称,则点B的坐标为
10.在平面直角坐标系中,点P在x轴的上侧,在y轴的左侧,距离每个坐标轴都是4个单位,则点P关于y轴的对称点P′的坐标为 .
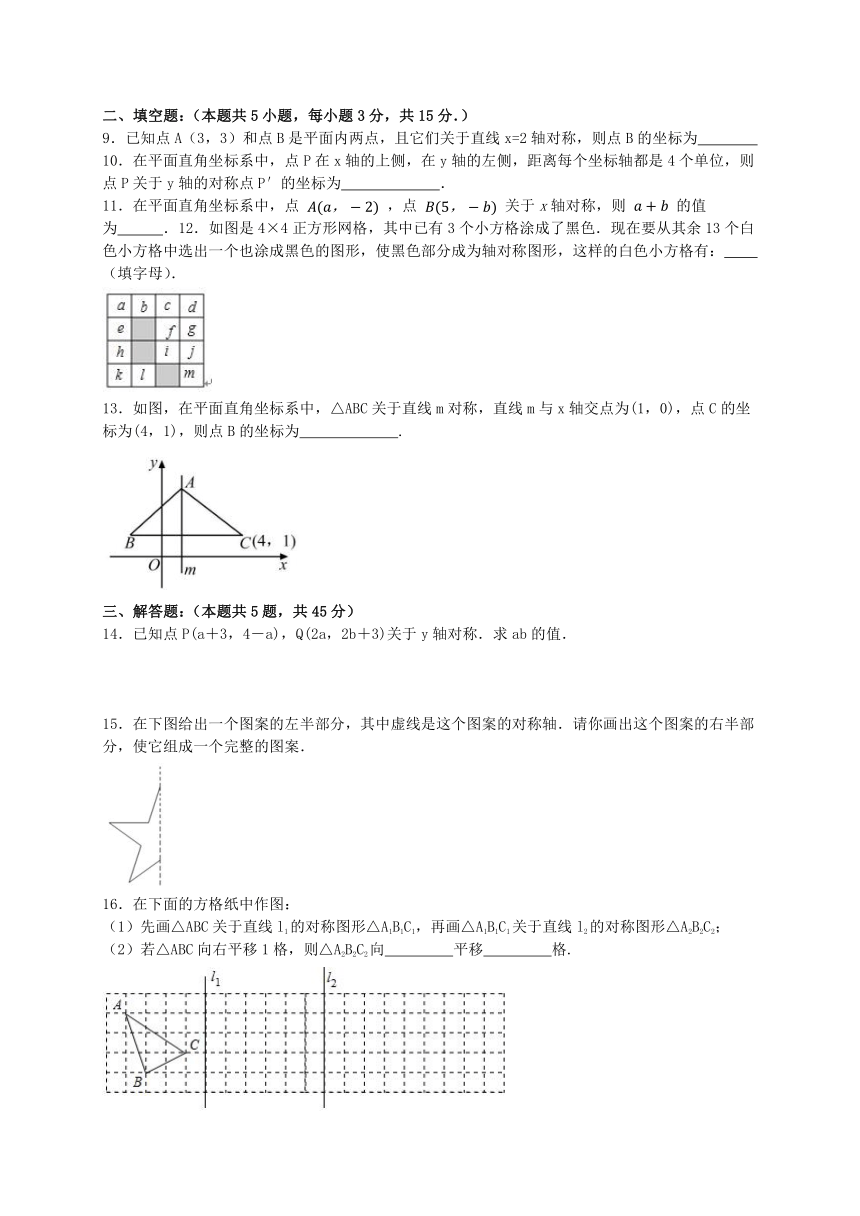
11.在平面直角坐标系中,点 ,点 关于x轴对称,则 的值为 .12.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形,使黑色部分成为轴对称图形,这样的白色小方格有: (填字母).
13.如图,在平面直角坐标系中,△ABC关于直线m对称,直线m与x轴交点为(1,0),点C的坐标为(4,1),则点B的坐标为 .
三、解答题:(本题共5题,共45分)
14.已知点P(a+3,4-a),Q(2a,2b+3)关于y轴对称.求ab的值.
15.在下图给出一个图案的左半部分,其中虚线是这个图案的对称轴.请你画出这个图案的右半部分,使它组成一个完整的图案.
16.在下面的方格纸中作图:
(1)先画△ABC关于直线l1的对称图形△A1B1C1,再画△A1B1C1关于直线l2的对称图形△A2B2C2;
(2)若△ABC向右平移1格,则△A2B2C2向 平移 格.
17.已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.
18.如图,已知线段,在平面直角坐标系中,且点A的坐标为.
(1)请在图中画出线段关于x轴对称的线段,并写出点的坐标;
(2)请在图中画出直线l,使得直线l是线段和线段的对称轴;
(3)在(2)的基础上,用无刻度的直尺和圆规在直线l上找一点P,使得.(保留作图痕迹,不要求写作法)
参考答案:
1.C 2.D 3.A 4.C 5.B 6.A 7.C 8.B
9.(1,3)
10.(4,4)
11.3
12.c,h,k,m.
13.(-2,1)
14.解:∵P(a+3,4-a),Q(2a,2b+3)关于y轴对称,
∴,
解得:,
∴ab=-1.
答:ab的值是-1.
15.解:根据轴对称图形的定义,画图如下(右边的实线部分):
16.(1)解:如图,△A1B1C1,△A2B2C2即为所求作.
(2)右;1
17.(1)解:描点如图,由题意得,AB∥x轴,且AB=3﹣(﹣2)=5,
∴S△ABC=×5×2=5
(2)解:如图;A′(﹣2,﹣1)、B′(3,﹣1)、C′(2,﹣3)
(3)解:M'(x,﹣y).
18.(1)解:根据题意可知B点坐标为(-4,1),
∵线段关于x轴对称的线段为
∴(-4,-1).
如图,线段即为所作;
(2)解:如图,直线l即为所作;
(3)解:如图,点P即为所求.
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列剪纸作品中,是轴对称图形的为( )
A. B. C. D.
2.若点A(3,-4)与点B(-3,a)关于y轴对称,则a的值为( )
A.3 B.-3 C.4 D.-4
3.若一个点A的横坐标不变,纵坐标乘以﹣1后得到一个点B,则( )
A.点A与点B关于x轴对称 B.点A与点B关于y轴对称
C.点A与点B关于原点对称 D.点A向x轴的负方向平移1个单位得点B
4.已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )
A.﹣1 B.1 C.﹣3 D.3
5.如图,在直角坐标系中,各点坐标分别为,,.先作关于x轴成轴对称的,再把平移后得到.若,则点坐标为( )
A. B. C. D.
6.在平面直角坐标系中,已知点A关于直线x=1对称的点为B(-2,4),则点A的坐标为( )
A.(4,4) B.(-2,-2) C.(2,4) D.(3,4)
7.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( )
A.(-3,2) B.(2,3) C.(2,-3) D.(-2,-3)
8.如图,正方形OABC对角线交点为D,过D的直线分别交AB,OC于E,F,已知点E关于y轴的对称点坐标为(﹣ ,2),则图中阴影部分的面积是( )
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知点A(3,3)和点B是平面内两点,且它们关于直线x=2轴对称,则点B的坐标为
10.在平面直角坐标系中,点P在x轴的上侧,在y轴的左侧,距离每个坐标轴都是4个单位,则点P关于y轴的对称点P′的坐标为 .
11.在平面直角坐标系中,点 ,点 关于x轴对称,则 的值为 .12.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形,使黑色部分成为轴对称图形,这样的白色小方格有: (填字母).
13.如图,在平面直角坐标系中,△ABC关于直线m对称,直线m与x轴交点为(1,0),点C的坐标为(4,1),则点B的坐标为 .
三、解答题:(本题共5题,共45分)
14.已知点P(a+3,4-a),Q(2a,2b+3)关于y轴对称.求ab的值.
15.在下图给出一个图案的左半部分,其中虚线是这个图案的对称轴.请你画出这个图案的右半部分,使它组成一个完整的图案.
16.在下面的方格纸中作图:
(1)先画△ABC关于直线l1的对称图形△A1B1C1,再画△A1B1C1关于直线l2的对称图形△A2B2C2;
(2)若△ABC向右平移1格,则△A2B2C2向 平移 格.
17.已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.
18.如图,已知线段,在平面直角坐标系中,且点A的坐标为.
(1)请在图中画出线段关于x轴对称的线段,并写出点的坐标;
(2)请在图中画出直线l,使得直线l是线段和线段的对称轴;
(3)在(2)的基础上,用无刻度的直尺和圆规在直线l上找一点P,使得.(保留作图痕迹,不要求写作法)
参考答案:
1.C 2.D 3.A 4.C 5.B 6.A 7.C 8.B
9.(1,3)
10.(4,4)
11.3
12.c,h,k,m.
13.(-2,1)
14.解:∵P(a+3,4-a),Q(2a,2b+3)关于y轴对称,
∴,
解得:,
∴ab=-1.
答:ab的值是-1.
15.解:根据轴对称图形的定义,画图如下(右边的实线部分):
16.(1)解:如图,△A1B1C1,△A2B2C2即为所求作.
(2)右;1
17.(1)解:描点如图,由题意得,AB∥x轴,且AB=3﹣(﹣2)=5,
∴S△ABC=×5×2=5
(2)解:如图;A′(﹣2,﹣1)、B′(3,﹣1)、C′(2,﹣3)
(3)解:M'(x,﹣y).
18.(1)解:根据题意可知B点坐标为(-4,1),
∵线段关于x轴对称的线段为
∴(-4,-1).
如图,线段即为所作;
(2)解:如图,直线l即为所作;
(3)解:如图,点P即为所求.
