11.3多边形及其内角和 同步练习 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.3多边形及其内角和 同步练习 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 107.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 21:16:08 | ||
图片预览

文档简介
11.3多边形及其内角和 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.一个正n边形的每个外角均为40°,则n=( )
A.6 B.7 C.8 D.9
2.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
4.如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
A.90° B.180° C.120° D.270°
5.在一次中学生科技制作展示赛上,蕲春县代表队一位模型赛车手遥控一辆赛车,先前进一米,然后原地逆时针方向旋转a°(0A.72° B.108°或144°
C.144° D.72°或144°
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )
A.400 B.450 C.500 D.600
7.如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
A.∠1=∠2>∠3 B.∠1=∠3>∠2
C.∠2>∠1=∠3 D.∠3>∠1=∠2
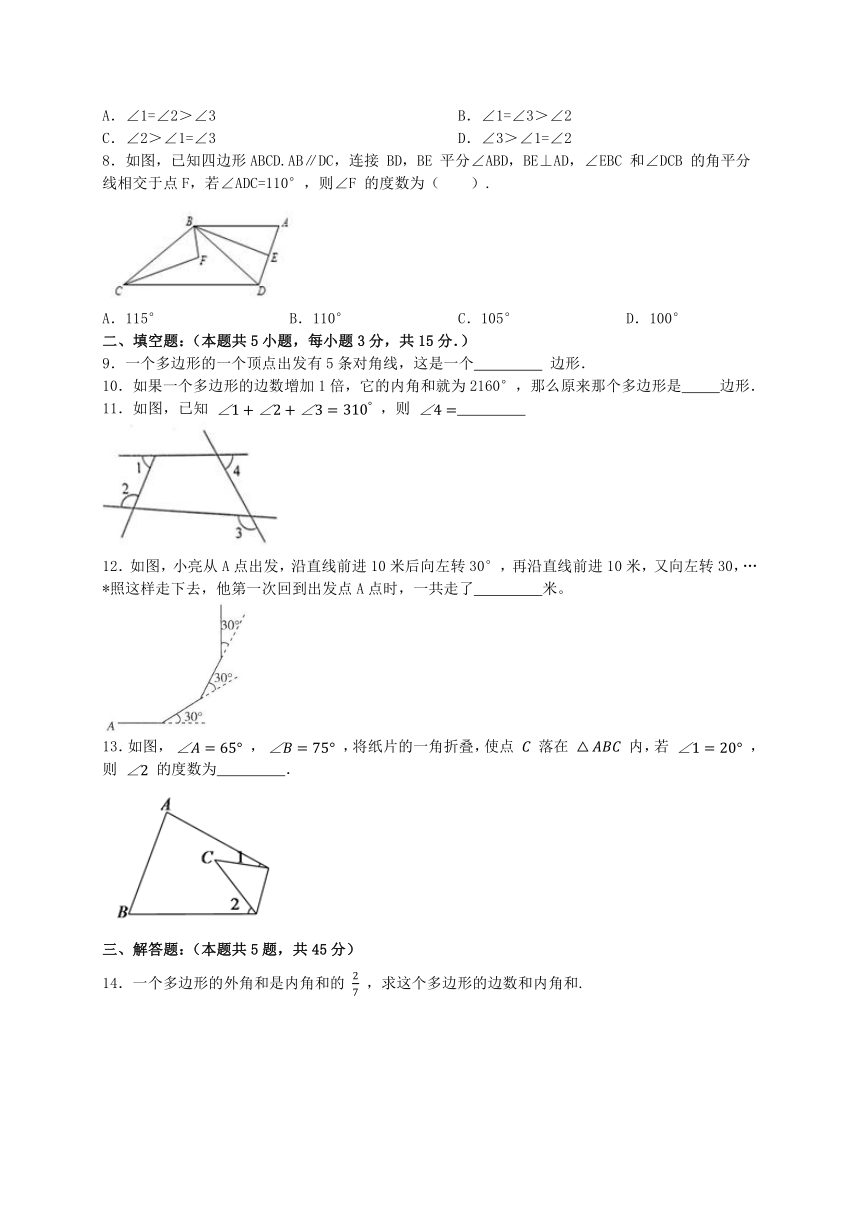
8.如图,已知四边形ABCD.AB∥DC,连接 BD,BE 平分∠ABD,BE⊥AD,∠EBC 和∠DCB 的角平分线相交于点F,若∠ADC=110°,则∠F 的度数为( ).
A.115° B.110° C.105° D.100°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.一个多边形的一个顶点出发有5条对角线,这是一个 边形.
10.如果一个多边形的边数增加1倍,它的内角和就为2160°,那么原来那个多边形是 边形.
11.如图,已知 ,则
12.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30,…*照这样走下去,他第一次回到出发点A点时,一共走了 米。
13.如图, , ,将纸片的一角折叠,使点 落在 内,若 ,则 的度数为 .
三、解答题:(本题共5题,共45分)
14.一个多边形的外角和是内角和的 ,求这个多边形的边数和内角和.
15.如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
16.小红把一副直角三角板按如图所示的方式摆放在一起,其中 , , , ,求 的度数.
17.如图.
(1)求图形中的x的值;
(2)求:∠A、∠B、∠C、∠D的度数.
18.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
参考答案:
1.D 2.C 3.C 4.B 5.D 6.A 7.D 8.D
9.八
10.七
11.50°
12.120
13.60°
14.解:设这个多边形的边数为n,
依题意得: (n﹣2)180°=360°,
解得n=9,
所以内角和为(9﹣2)180°=1260°.
答:这个多边形的边数为9,内角和为1260°.
15.解:
又∵ 四边形 的内角和为:
平分 , 平分
16.解:如图,由三角形的外角的性质可得:
17.(1)解:依题意有:
3x+3x+4x+2x=360°,
解得x=30°
(2)解:∠A=∠B=3×30°=90°,
∠C=2×30°=60°,
∠D=4×30°=120°
18.(1)证明:AD∥BC,
∠ADC+∠BCD=180°,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°;
(2)解:∵∠FBD+∠BDE=90°-∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.一个正n边形的每个外角均为40°,则n=( )
A.6 B.7 C.8 D.9
2.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
4.如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
A.90° B.180° C.120° D.270°
5.在一次中学生科技制作展示赛上,蕲春县代表队一位模型赛车手遥控一辆赛车,先前进一米,然后原地逆时针方向旋转a°(0
C.144° D.72°或144°
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )
A.400 B.450 C.500 D.600
7.如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
A.∠1=∠2>∠3 B.∠1=∠3>∠2
C.∠2>∠1=∠3 D.∠3>∠1=∠2
8.如图,已知四边形ABCD.AB∥DC,连接 BD,BE 平分∠ABD,BE⊥AD,∠EBC 和∠DCB 的角平分线相交于点F,若∠ADC=110°,则∠F 的度数为( ).
A.115° B.110° C.105° D.100°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.一个多边形的一个顶点出发有5条对角线,这是一个 边形.
10.如果一个多边形的边数增加1倍,它的内角和就为2160°,那么原来那个多边形是 边形.
11.如图,已知 ,则
12.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30,…*照这样走下去,他第一次回到出发点A点时,一共走了 米。
13.如图, , ,将纸片的一角折叠,使点 落在 内,若 ,则 的度数为 .
三、解答题:(本题共5题,共45分)
14.一个多边形的外角和是内角和的 ,求这个多边形的边数和内角和.
15.如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
16.小红把一副直角三角板按如图所示的方式摆放在一起,其中 , , , ,求 的度数.
17.如图.
(1)求图形中的x的值;
(2)求:∠A、∠B、∠C、∠D的度数.
18.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
参考答案:
1.D 2.C 3.C 4.B 5.D 6.A 7.D 8.D
9.八
10.七
11.50°
12.120
13.60°
14.解:设这个多边形的边数为n,
依题意得: (n﹣2)180°=360°,
解得n=9,
所以内角和为(9﹣2)180°=1260°.
答:这个多边形的边数为9,内角和为1260°.
15.解:
又∵ 四边形 的内角和为:
平分 , 平分
16.解:如图,由三角形的外角的性质可得:
17.(1)解:依题意有:
3x+3x+4x+2x=360°,
解得x=30°
(2)解:∠A=∠B=3×30°=90°,
∠C=2×30°=60°,
∠D=4×30°=120°
18.(1)证明:AD∥BC,
∠ADC+∠BCD=180°,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°;
(2)解:∵∠FBD+∠BDE=90°-∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°
