2023-2024学年人教版数学八年级上册1.3.1 多边形 教学设计(表格式)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册1.3.1 多边形 教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 08:31:45 | ||
图片预览

文档简介
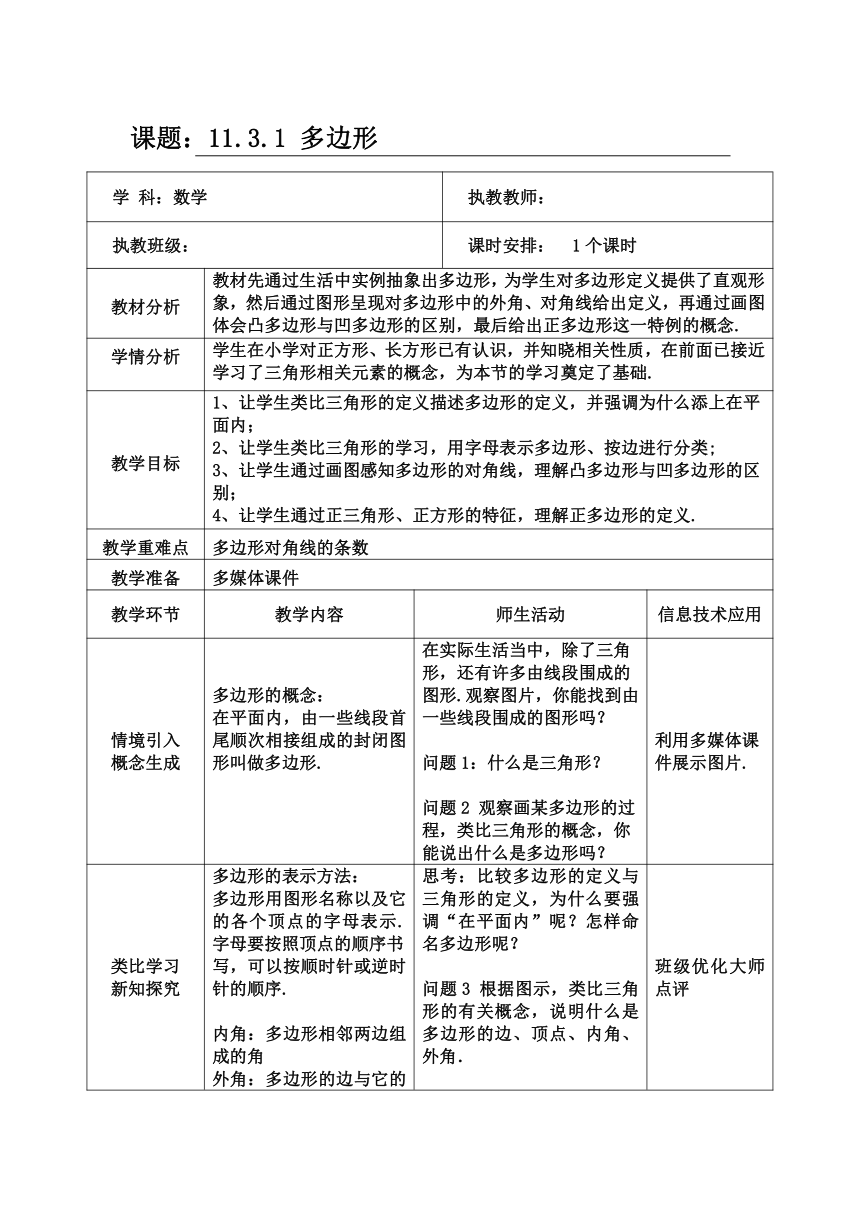
课题:11.3.1 多边形
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材先通过生活中实例抽象出多边形,为学生对多边形定义提供了直观形象,然后通过图形呈现对多边形中的外角、对角线给出定义,再通过画图体会凸多边形与凹多边形的区别,最后给出正多边形这一特例的概念.
学情分析 学生在小学对正方形、长方形已有认识,并知晓相关性质,在前面已接近学习了三角形相关元素的概念,为本节的学习奠定了基础.
教学目标 1、让学生类比三角形的定义描述多边形的定义,并强调为什么添上在平面内; 2、让学生类比三角形的学习,用字母表示多边形、按边进行分类; 3、让学生通过画图感知多边形的对角线,理解凸多边形与凹多边形的区别; 4、让学生通过正三角形、正方形的特征,理解正多边形的定义.
教学重难点 多边形对角线的条数
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
情境引入 概念生成 多边形的概念: 在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形. 在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗? 问题1:什么是三角形? 问题2 观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗? 利用多媒体课件展示图片.
类比学习 新知探究 多边形的表示方法: 多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书 写,可以按顺时针或逆时针的顺序. 内角:多边形相邻两边组成的角 外角:多边形的边与它的邻边的延长线组成的角. 多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形. 画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形. 思考:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢? 问题3 根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角. 问题4 请分别画出下列两个图形各边所在的直线 , 你能得到什么结论? 班级优化大师点评 希沃授课助手投屏展示
典例讲解 巩固知识 例1 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明. 教师引导学生画图: 学生回答:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,∴新多边形的边数为7,5,6三种情况, 师生总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条. 利用授课助手投屏展示学生画图. .
再探新知 发现规律 连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形. n(n≥3)边形共有对角线 条. 教师说明:线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示. 探究:请画出下列图形从某一顶点出发的对角线的条数 : 班级优化大师随机抽选、小组点评.
典例讲解 巩固知识 例2 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数. 学生回答:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2, ∴n-3+n-2=21, 解得n=13. 答:该多边形的边数有13条. 利用班级优化大师点评
特例学习 再探新知 定义: 像正方形这样,各个角都相等,各条边都相等的多边形. 注意: 判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备. 想一想:下列多边形是正多边形吗?如不是,请说明为什么? 学生回答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等. 课件展示
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 思维导图展示
学情反馈 布置作业 课本第21页练习1、2; 2.基训上本课时习题。 学生课后完成,教师批改、讲评.
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材先通过生活中实例抽象出多边形,为学生对多边形定义提供了直观形象,然后通过图形呈现对多边形中的外角、对角线给出定义,再通过画图体会凸多边形与凹多边形的区别,最后给出正多边形这一特例的概念.
学情分析 学生在小学对正方形、长方形已有认识,并知晓相关性质,在前面已接近学习了三角形相关元素的概念,为本节的学习奠定了基础.
教学目标 1、让学生类比三角形的定义描述多边形的定义,并强调为什么添上在平面内; 2、让学生类比三角形的学习,用字母表示多边形、按边进行分类; 3、让学生通过画图感知多边形的对角线,理解凸多边形与凹多边形的区别; 4、让学生通过正三角形、正方形的特征,理解正多边形的定义.
教学重难点 多边形对角线的条数
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
情境引入 概念生成 多边形的概念: 在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形. 在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗? 问题1:什么是三角形? 问题2 观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗? 利用多媒体课件展示图片.
类比学习 新知探究 多边形的表示方法: 多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书 写,可以按顺时针或逆时针的顺序. 内角:多边形相邻两边组成的角 外角:多边形的边与它的邻边的延长线组成的角. 多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形. 画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形. 思考:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢? 问题3 根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角. 问题4 请分别画出下列两个图形各边所在的直线 , 你能得到什么结论? 班级优化大师点评 希沃授课助手投屏展示
典例讲解 巩固知识 例1 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明. 教师引导学生画图: 学生回答:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,∴新多边形的边数为7,5,6三种情况, 师生总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条. 利用授课助手投屏展示学生画图. .
再探新知 发现规律 连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形. n(n≥3)边形共有对角线 条. 教师说明:线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示. 探究:请画出下列图形从某一顶点出发的对角线的条数 : 班级优化大师随机抽选、小组点评.
典例讲解 巩固知识 例2 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21,求这个多边形的边数. 学生回答:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2, ∴n-3+n-2=21, 解得n=13. 答:该多边形的边数有13条. 利用班级优化大师点评
特例学习 再探新知 定义: 像正方形这样,各个角都相等,各条边都相等的多边形. 注意: 判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备. 想一想:下列多边形是正多边形吗?如不是,请说明为什么? 学生回答:都不是,第一个图形不符合四个角都相等;第二个图形不符合各边都相等. 课件展示
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 思维导图展示
学情反馈 布置作业 课本第21页练习1、2; 2.基训上本课时习题。 学生课后完成,教师批改、讲评.
