人教版数学八年级上册 15.2分式的加减第3课时 整数指数幂课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 15.2分式的加减第3课时 整数指数幂课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 722.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
15.2 分式的加减
第3课时 整数指数幂
1.理解负整数指数幂的意义.
2.熟练应用整数指数幂的运算性质进行计算.
3.会用科学记数法表示小于1的正小数.
教学目标
回忆正整数指数幂的运算性质
(1)
(2)
(3)
(4)
(5)
______.(m,n是正整数);
_____. (m,n是正整数);
______.(n是正整数);
_____.(a≠0,m,n是正整数,m>n);
____.(n是正整数)
还有上一章学的
_____.(a≠0)
复习回顾
1
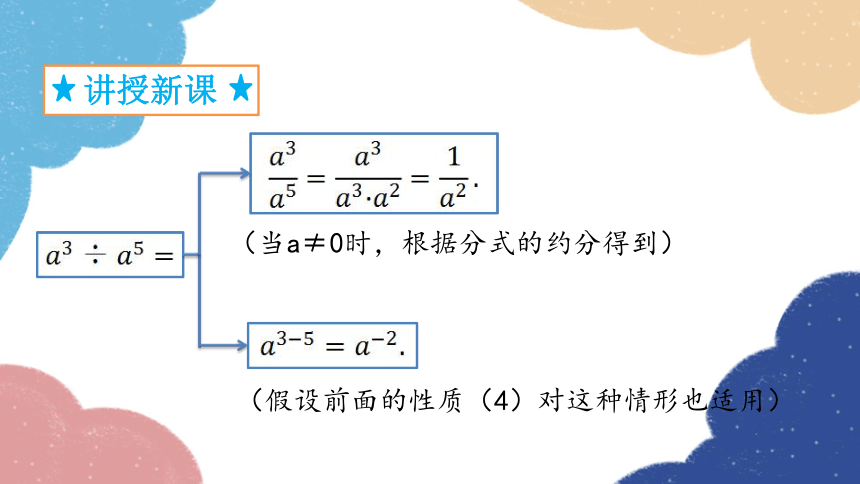
(当a≠0时,根据分式的约分得到)
(假设前面的性质(4)对这种情形也适用)
讲授新课
因此数学中规定
试想,如果规定
(a≠0)就能使
这条性质也适用于像
思考:正整数指数幂的运算性质是否满足全体整数?
先分析一下 这条性质(从特殊情形入手研究).
即
即
即
类似的,我们用负整数指数幂或0指数幂对其他正整数
指数幂的运算性质进行试验,可以发现这些运算性质
在整数指数幂范围内也适用.
试着自己证明这些运算性质吧
根据整数指数幂的运算性质,当m、n为整数时
所以整数指数幂的运算性质可以归结为:
例1 计算:
解:
典例精讲
解:
例1 计算:
典例精讲
…………………………
0.00···01
n个0
讲授新课
填空:
n个0
n个0
n个0
思考:大于-1小于0的负数,是否也可以用科学记数法表示?
例2 用科学记数法表示下列各数:
(1)0.000000001;
(2)0.0012;
(3)0.0000000108.
典例精讲
对于一个小于1的正小数,从小数点前第一个0算起至小数
点后第一个非0数字前有几个0,用科学记数法表示这个数时,
10的指数就是负几.
解:
典例精讲
课堂练习
1.下列计算正确的是( )
D.
D
2.下列计算正确的是( )
C
解:
解:
4.用科学记数法表示下列各数:
(1)0.00001;
(2)0.000000567;
(3)0.000000301.
解:
5.计算:
(1)
(2)
解:
(1)
(2)
课堂小结
回顾一下今天学习了哪些知识:
1.负整数指数幂的式子表示.
2.整数指数幂的运算性质.
3.如何用科学记数法表示小于1的正数.
15.2 分式的加减
第3课时 整数指数幂
1.理解负整数指数幂的意义.
2.熟练应用整数指数幂的运算性质进行计算.
3.会用科学记数法表示小于1的正小数.
教学目标
回忆正整数指数幂的运算性质
(1)
(2)
(3)
(4)
(5)
______.(m,n是正整数);
_____. (m,n是正整数);
______.(n是正整数);
_____.(a≠0,m,n是正整数,m>n);
____.(n是正整数)
还有上一章学的
_____.(a≠0)
复习回顾
1
(当a≠0时,根据分式的约分得到)
(假设前面的性质(4)对这种情形也适用)
讲授新课
因此数学中规定
试想,如果规定
(a≠0)就能使
这条性质也适用于像
思考:正整数指数幂的运算性质是否满足全体整数?
先分析一下 这条性质(从特殊情形入手研究).
即
即
即
类似的,我们用负整数指数幂或0指数幂对其他正整数
指数幂的运算性质进行试验,可以发现这些运算性质
在整数指数幂范围内也适用.
试着自己证明这些运算性质吧
根据整数指数幂的运算性质,当m、n为整数时
所以整数指数幂的运算性质可以归结为:
例1 计算:
解:
典例精讲
解:
例1 计算:
典例精讲
…………………………
0.00···01
n个0
讲授新课
填空:
n个0
n个0
n个0
思考:大于-1小于0的负数,是否也可以用科学记数法表示?
例2 用科学记数法表示下列各数:
(1)0.000000001;
(2)0.0012;
(3)0.0000000108.
典例精讲
对于一个小于1的正小数,从小数点前第一个0算起至小数
点后第一个非0数字前有几个0,用科学记数法表示这个数时,
10的指数就是负几.
解:
典例精讲
课堂练习
1.下列计算正确的是( )
D.
D
2.下列计算正确的是( )
C
解:
解:
4.用科学记数法表示下列各数:
(1)0.00001;
(2)0.000000567;
(3)0.000000301.
解:
5.计算:
(1)
(2)
解:
(1)
(2)
课堂小结
回顾一下今天学习了哪些知识:
1.负整数指数幂的式子表示.
2.整数指数幂的运算性质.
3.如何用科学记数法表示小于1的正数.
