华师大版数学八年级上册 13.3.2等腰三角形的判定 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级上册 13.3.2等腰三角形的判定 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 182.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 09:35:24 | ||
图片预览




文档简介
(共16张PPT)
13.3.2 等腰三角形的判定
一、复习回顾
等腰三角形的已有认识:
1、从边看:等腰三角形的两腰相等。(定义)
2、从角看:等腰三角形的两底角相等。
(性质定理1——等边对等角)
3、从重要线段看:等腰三角形的顶角平分线、 底边上的中线和底边上的高。
(性质定理2—三线合一)
4、从对称性看:
等腰三角形是轴对称图形。
定义:有两边相等的三角形是等腰三角形。
如何判定一个三角形是等腰三角形?
还有其他方法吗?
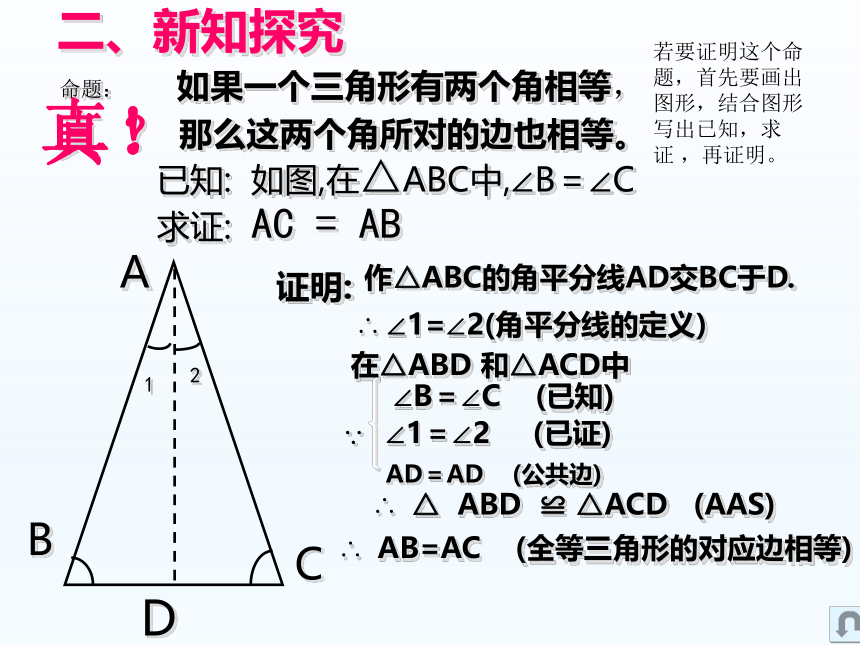
二、新知探究
命题:
如果一个三角形有两个角相等,
那么这两个角所对的边也相等。
真 ?
已知: 如图,在△ABC中,∠B=∠C
A
B
C
求证: AC = AB
D
1
2
证明:
作△ABC的角平分线AD交BC于D.
在△ABD 和△ACD中
∵
∠B=∠C (已知)
AD=AD (公共边)
∠1=∠2 (已证)
∴ △ ABD ≌ △ACD (AAS)
∴ AB=AC (全等三角形的对应边相等)
∴ ∠1=∠2(角平分线的定义)
若要证明这个命题,首先要画出图形,结合图形写出已知,求证 ,再证明。
真!
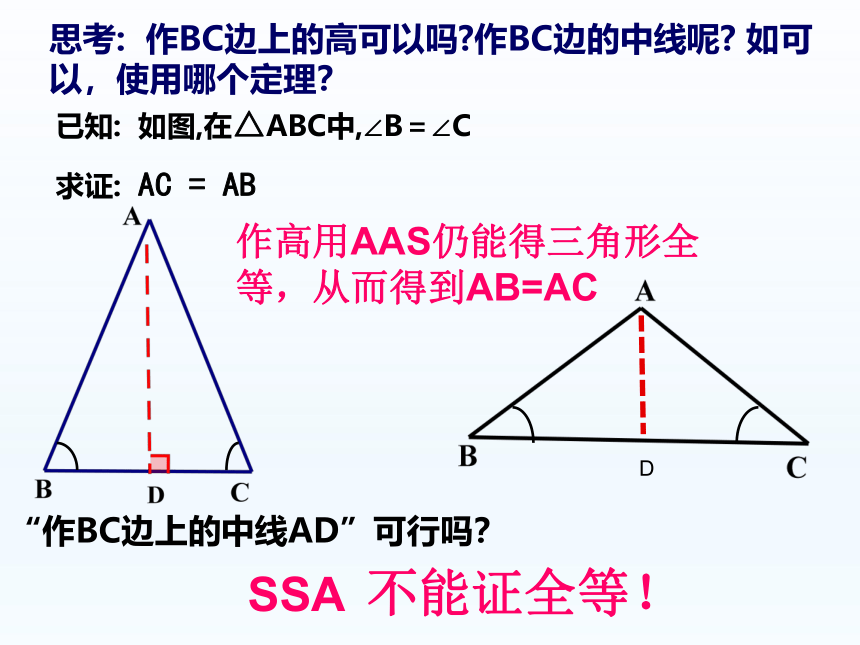
思考: 作BC边上的高可以吗 作BC边的中线呢 如可以,使用哪个定理?
“作BC边上的中线AD”可行吗?
SSA 不能证全等!
作高用AAS仍能得三角形全等,从而得到AB=AC
已知: 如图,在△ABC中,∠B=∠C
求证: AC = AB
D
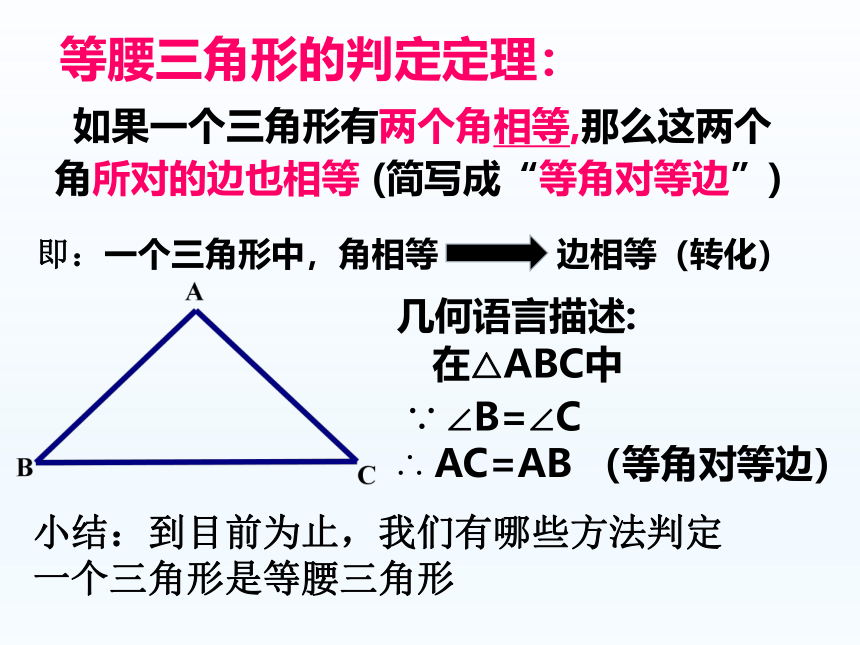
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个
角所对的边也相等 (简写成“等角对等边”)
小结:到目前为止,我们有哪些方法判定一个三角形是等腰三角形
即:一个三角形中,角相等
边相等(转化)
几何语言描述:
在△ABC中
∵ ∠B=∠C
∴ AC=AB (等角对等边)
例1.填一填:
已知:如图,∠A=36°,∠DBC =36°, ∠C=72°,则∠1= ,∠2= ,图中等腰三角形有 .
小结:通过计算发现角度相等,运用一个三角形中等角对等边获得边相等而判断等腰三角形.
△ABC、△BCD、△ABD
72°
36°
三、新知运用
36°
72°
36°
例2:如图:已知△ABC中,点D、E在BC边上,AD=AE,∠1=∠2,求证:AB=AC
小结:证线段相等,放在一个三角形中可探寻等角,说明等边;放在两个三角形中可用全等获得.
分析:要证明AB=AC,通过图形观察:
①如果AB、AC放在两个三角形中,考虑用什么知识解决?
②如果AB、AC放在一个三角形中,考虑用什么知识解决?
例3:如图,在△ABC中∠ABC和∠ACB的角平分线相交于点O,过点O作DE∥BC交AB于点D,交AC于点E。
⑴:请猜想DE、BD、CE之间的数量关系,并说明理由____________⑵:若AB=7,AC=5,BC=8,求△ADE的周长。
DE=BD+CE
小结:
已知条件有角平分线和平行线常常可构成等腰三角形
即 DE = BD + CE
解⑴∵BO是∠ABC的平分线(已知)
∴∠1=∠2 (角平分线的定义)
∵DE∥BC (已知)
∴∠2=∠3 (两直线平行内错角相等)
∴∠1=∠3 (等量代换)
∴OD=BD (等角对等边)
同理得 OE=CE
∴OD+OE=BD+CE(等式的性质)
例3:如图,在△ABC中∠ABC和∠ACB的角平分线相交于点O,过点O作DE∥BC交AB于点D,交AC于点E。
⑴:DE、BD、CE之间的数量关系____________
⑵:若AB=7,AC=5,BC=8,求△ADE的周长。
DE=BD+CE
解⑵:△ADE的周长 =AD+AE+DE
由结论⑴可知DE=BD+CE
∴△ADE的周长 =AD+AE+BD+CE
=(AD+BD)+(AE+CE)
=AB+AC
=7+5
=12
2、等腰三角形的判定方法有下列几种: 。
3、等腰三角形的判定定理与性质定理的区别是 。
4、运用等腰三角形的判定定理时,应注意 。
①定义,②判定定理
条件和结论刚好互换位置
等角在同一个三角形中
四、课堂小结:
5、主要思想方法: .
转化
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
1、等腰三角形判定定理
1:在△ABC中,∠A的相邻外角是80 ,要使△ABC为等腰三角形,需要∠B=_______
五、学以致用:
若把∠A的邻角80 改为130 呢?
需要∠B= .
40
本题小结:1、知识:2、主要思想方法:分类讨论
65
或 50
或 80°
2.如图在Rt△ABC中,在斜边AB和直角边AC上分别取一点D、E,使DE=DA,延长DE交BC的延长线于点F,△DFB是等腰三角形吗?请说明你的理由。
答:△DFB是等腰三角形. 理由如下:
∵ △ABC是 Rt△、AB是斜边
∴∠ACB = 90°(直角三角形定义)
∴∠ECF = 90°
在△ADE中
∵ DE=DA (已知)
∴∠A = ∠AED (等边对等角)
又∵∠AED =∠CEF (对顶角相等)
∴∠A = ∠CEF (等量代换)
∴ ∠B = ∠F ( 等角的余角相等)
∴ DF = DB (等角对等边)
∴ △DFB是等腰三角形.
解答书写思路:结论------理由
3、如图,C表示灯塔,轮船从A处出发以每时20海里的速度向正北(AM方向)航行,2时后到达B处。测得C在A的北偏西37 方向,并在B的北偏西74 方向,求B处到灯塔C的距离。
解:
由题意得:
∠A=37°,∠MBC=74°,AB=40.
∴∠C = 37°( )
∴ ∠A = ∠C ( 等量代换)
∴ BC = AB = 40 (等角对等边)
答:B处到灯塔C的距离为 40海里.
4、如图,已知矩形ABCD,现将△CBD沿BD翻折至△C'BD的位置,且DC'与AB交于点M
试证明:MD=MB
5.如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF,求证DE=DF
(考虑添加辅助线)
13.3.2 等腰三角形的判定
一、复习回顾
等腰三角形的已有认识:
1、从边看:等腰三角形的两腰相等。(定义)
2、从角看:等腰三角形的两底角相等。
(性质定理1——等边对等角)
3、从重要线段看:等腰三角形的顶角平分线、 底边上的中线和底边上的高。
(性质定理2—三线合一)
4、从对称性看:
等腰三角形是轴对称图形。
定义:有两边相等的三角形是等腰三角形。
如何判定一个三角形是等腰三角形?
还有其他方法吗?
二、新知探究
命题:
如果一个三角形有两个角相等,
那么这两个角所对的边也相等。
真 ?
已知: 如图,在△ABC中,∠B=∠C
A
B
C
求证: AC = AB
D
1
2
证明:
作△ABC的角平分线AD交BC于D.
在△ABD 和△ACD中
∵
∠B=∠C (已知)
AD=AD (公共边)
∠1=∠2 (已证)
∴ △ ABD ≌ △ACD (AAS)
∴ AB=AC (全等三角形的对应边相等)
∴ ∠1=∠2(角平分线的定义)
若要证明这个命题,首先要画出图形,结合图形写出已知,求证 ,再证明。
真!
思考: 作BC边上的高可以吗 作BC边的中线呢 如可以,使用哪个定理?
“作BC边上的中线AD”可行吗?
SSA 不能证全等!
作高用AAS仍能得三角形全等,从而得到AB=AC
已知: 如图,在△ABC中,∠B=∠C
求证: AC = AB
D
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个
角所对的边也相等 (简写成“等角对等边”)
小结:到目前为止,我们有哪些方法判定一个三角形是等腰三角形
即:一个三角形中,角相等
边相等(转化)
几何语言描述:
在△ABC中
∵ ∠B=∠C
∴ AC=AB (等角对等边)
例1.填一填:
已知:如图,∠A=36°,∠DBC =36°, ∠C=72°,则∠1= ,∠2= ,图中等腰三角形有 .
小结:通过计算发现角度相等,运用一个三角形中等角对等边获得边相等而判断等腰三角形.
△ABC、△BCD、△ABD
72°
36°
三、新知运用
36°
72°
36°
例2:如图:已知△ABC中,点D、E在BC边上,AD=AE,∠1=∠2,求证:AB=AC
小结:证线段相等,放在一个三角形中可探寻等角,说明等边;放在两个三角形中可用全等获得.
分析:要证明AB=AC,通过图形观察:
①如果AB、AC放在两个三角形中,考虑用什么知识解决?
②如果AB、AC放在一个三角形中,考虑用什么知识解决?
例3:如图,在△ABC中∠ABC和∠ACB的角平分线相交于点O,过点O作DE∥BC交AB于点D,交AC于点E。
⑴:请猜想DE、BD、CE之间的数量关系,并说明理由____________⑵:若AB=7,AC=5,BC=8,求△ADE的周长。
DE=BD+CE
小结:
已知条件有角平分线和平行线常常可构成等腰三角形
即 DE = BD + CE
解⑴∵BO是∠ABC的平分线(已知)
∴∠1=∠2 (角平分线的定义)
∵DE∥BC (已知)
∴∠2=∠3 (两直线平行内错角相等)
∴∠1=∠3 (等量代换)
∴OD=BD (等角对等边)
同理得 OE=CE
∴OD+OE=BD+CE(等式的性质)
例3:如图,在△ABC中∠ABC和∠ACB的角平分线相交于点O,过点O作DE∥BC交AB于点D,交AC于点E。
⑴:DE、BD、CE之间的数量关系____________
⑵:若AB=7,AC=5,BC=8,求△ADE的周长。
DE=BD+CE
解⑵:△ADE的周长 =AD+AE+DE
由结论⑴可知DE=BD+CE
∴△ADE的周长 =AD+AE+BD+CE
=(AD+BD)+(AE+CE)
=AB+AC
=7+5
=12
2、等腰三角形的判定方法有下列几种: 。
3、等腰三角形的判定定理与性质定理的区别是 。
4、运用等腰三角形的判定定理时,应注意 。
①定义,②判定定理
条件和结论刚好互换位置
等角在同一个三角形中
四、课堂小结:
5、主要思想方法: .
转化
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
1、等腰三角形判定定理
1:在△ABC中,∠A的相邻外角是80 ,要使△ABC为等腰三角形,需要∠B=_______
五、学以致用:
若把∠A的邻角80 改为130 呢?
需要∠B= .
40
本题小结:1、知识:2、主要思想方法:分类讨论
65
或 50
或 80°
2.如图在Rt△ABC中,在斜边AB和直角边AC上分别取一点D、E,使DE=DA,延长DE交BC的延长线于点F,△DFB是等腰三角形吗?请说明你的理由。
答:△DFB是等腰三角形. 理由如下:
∵ △ABC是 Rt△、AB是斜边
∴∠ACB = 90°(直角三角形定义)
∴∠ECF = 90°
在△ADE中
∵ DE=DA (已知)
∴∠A = ∠AED (等边对等角)
又∵∠AED =∠CEF (对顶角相等)
∴∠A = ∠CEF (等量代换)
∴ ∠B = ∠F ( 等角的余角相等)
∴ DF = DB (等角对等边)
∴ △DFB是等腰三角形.
解答书写思路:结论------理由
3、如图,C表示灯塔,轮船从A处出发以每时20海里的速度向正北(AM方向)航行,2时后到达B处。测得C在A的北偏西37 方向,并在B的北偏西74 方向,求B处到灯塔C的距离。
解:
由题意得:
∠A=37°,∠MBC=74°,AB=40.
∴∠C = 37°( )
∴ ∠A = ∠C ( 等量代换)
∴ BC = AB = 40 (等角对等边)
答:B处到灯塔C的距离为 40海里.
4、如图,已知矩形ABCD,现将△CBD沿BD翻折至△C'BD的位置,且DC'与AB交于点M
试证明:MD=MB
5.如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF,求证DE=DF
(考虑添加辅助线)
